 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Тема 11. Провідник в електричному полі
Задачі (44) Покажемо, що в провіднику, поміщеному в електричне поле, воно дорівнюватиме нулеві, а за межами провідника – зміниться.
Очевидно: якщо провідник порожнистий, то нічого від цього не зміниться, поле всередині такої провідної посудини відсутнє. Це явище використовують для захисту електричних приладів від зовнішнього електричного поля. Для цього прилади поміщають у металеві корпуси.
(45) Покажемо: якщо провіднику надати заряду, то він розміститься на його поверхні.
(46) Покажемо, що як заряджений так і електронейтральний провідник є еквіпотенціяльним. Оскільки заряд розміщується на поверхні провідника, то поле всередині провідника відсутнє. Дійсно, виберемо замкнену поверхню всередині провідника (мал. 35). Так як в області, обмеженій цією поверхнею, немає зарядів, то згідно з теоремою Остроградського–Гауса
звідки, оскільки
З останньої рівності випливає, що
з формули зв’язку напруженості з потенціялом
звідки робимо висновок, що
(47) Доведемо, що електричне поле між точковим зарядом та нескінченною провідною площиною збігається з полем, створеним цим зарядом, та його дзеркальним зображенням у цій площині. Будемо доводити навпаки, що поле двох точкових різнойменних зарядів (поле диполя) можна замінити на поле одного заряду та провідної не зарядженої площини.
Бачимо, що таким способом можна встановити картину силових ліній поля, створеного точковим зарядом та незарядженою провідною площиною. Цей спосіб має назву: метод дзеркальних зображень.
Поиск по сайту: |
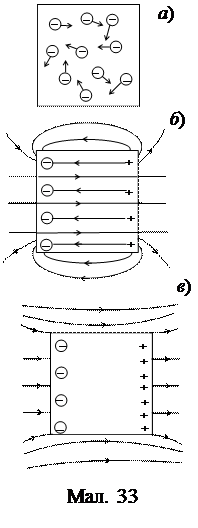 Візьмемо конкретний провідник – метал. Відомо, що в ньому є вільні носії заряду – електрони (мал. 33, а), які рухаються хаотично. Як тільки ми включимо електростатичне поле, воно почне діяти на вільні електрони, і вони, маючи негативний заряд, почнуть рухатися проти силових ліній. У результаті їх нагромадження на одній з поверхонь, на протилежній поверхні (а точніше в усьому об’ємі) виникне нескомпенсований позитивний заряд, що стане причиною виникнення внутрішнього електричного поля, спрямованого протилежно до зовнішнього (мал. 33, б). Проте в міру нагромадження електронів на поверхні, внутрішнє поле буде зростати і все більше гальмувати інші електрони в їхньому русі проти зовнішнього поля. Коли внутрішнє поле зросте настільки, що воно зрівняється за величиною з зовнішнім, рух електронів припиниться. Оскільки напрями цих полів протилежні, то поле всередині провідника зникне (мал. 33, в). За межами провідника зліва і справа поле індукованих зарядів буде співнаправлене із зовнішнім полем, тому підсилить його. Проте зверху і знизу силові лінії здеформуються і густота їхня стане меншою, що означає, що там поле послаблюється.
Візьмемо конкретний провідник – метал. Відомо, що в ньому є вільні носії заряду – електрони (мал. 33, а), які рухаються хаотично. Як тільки ми включимо електростатичне поле, воно почне діяти на вільні електрони, і вони, маючи негативний заряд, почнуть рухатися проти силових ліній. У результаті їх нагромадження на одній з поверхонь, на протилежній поверхні (а точніше в усьому об’ємі) виникне нескомпенсований позитивний заряд, що стане причиною виникнення внутрішнього електричного поля, спрямованого протилежно до зовнішнього (мал. 33, б). Проте в міру нагромадження електронів на поверхні, внутрішнє поле буде зростати і все більше гальмувати інші електрони в їхньому русі проти зовнішнього поля. Коли внутрішнє поле зросте настільки, що воно зрівняється за величиною з зовнішнім, рух електронів припиниться. Оскільки напрями цих полів протилежні, то поле всередині провідника зникне (мал. 33, в). За межами провідника зліва і справа поле індукованих зарядів буде співнаправлене із зовнішнім полем, тому підсилить його. Проте зверху і знизу силові лінії здеформуються і густота їхня стане меншою, що означає, що там поле послаблюється.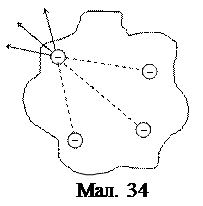 Припустимо, що заряд розподілився в об’ємі провідника. Тоді на будь-який заряд з боку інших однойменних зарядів буде діяти сила, яка спрямована до поверхні. А оскільки він може вільно переміщуватися, то почне рухатися до поверхні (мал. 34). Те саме станеться і з іншими зарядами. В результаті всі заряди розмістяться на поверхні провідника.
Припустимо, що заряд розподілився в об’ємі провідника. Тоді на будь-який заряд з боку інших однойменних зарядів буде діяти сила, яка спрямована до поверхні. А оскільки він може вільно переміщуватися, то почне рухатися до поверхні (мал. 34). Те саме станеться і з іншими зарядами. В результаті всі заряди розмістяться на поверхні провідника.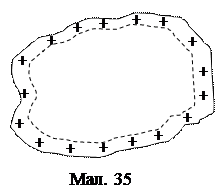
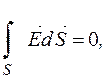
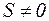
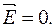
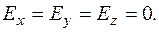
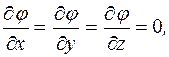
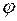 не залежить від координат, тобто всюди всередині зарядженого (чи не зарядженого) провідника
не залежить від координат, тобто всюди всередині зарядженого (чи не зарядженого) провідника 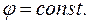
 Проведемо одну з еквіпотенціяльних поверхонь, а саме ту, яка проходить через середину плеча диполя, яка як відомо, є площиною (мал. 36). Замінимо тепер цю еквіпотенціяльну площину на реальну провідну площину з потенціялом, що дорівнює потенціялу еквіпотенціяльної площини. Очевидно, що від цього нічого не зміниться, поле залишиться таким самим.
Проведемо одну з еквіпотенціяльних поверхонь, а саме ту, яка проходить через середину плеча диполя, яка як відомо, є площиною (мал. 36). Замінимо тепер цю еквіпотенціяльну площину на реальну провідну площину з потенціялом, що дорівнює потенціялу еквіпотенціяльної площини. Очевидно, що від цього нічого не зміниться, поле залишиться таким самим.