 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Тема 6. Потік електричної індукції
Теорема Остроградського –Гауса Фізичні величини · Електрична індукція –це вектор
·
де Аналогічно означається потік напруженості електричного поля. Задачі
Розділимо цю поверхню на велику кількість нескінченно малих поверхонь площею Крім того, в межах цієї поверхні поле можна вважати однорідним. Таким чином до цієї нескінченно малої поверхні можна застосувати означення потоку однорідного поля через плоску поверхню
Очевидно, що потік через всю поверхню буде дорівнювати сумі потоків через всі поверхні площею
З цього виведення випливає також висновок про те, що потоки можна додавати, тобто оскільки площа поверхні
(20) Доведемо, що потік індукції електричного поля через певну поверхню пропорційний до кількості силових ліній, які її пронизують. Для доведення скористаємось тим фактом, що величина вектора електричної індукції пропорційна до густоти силових ліній (задача 8), тобто Згідно з означенням потоку, пропорційністю між
Отже,
що означає, що кількість силових ліній, які пронизують цю поверхню, вказує на величину потоку електричної індукції через неї. Згадаймо, що в гідроаеродинаміці є подібна ситуація: густота ліній потоку вказує на швидкість потоку, а кількість ліній потоку – на величину потоку, яка дорівнює об’єму рідини чи газу, що перетинає певний переріз за одиницю часу.
(21) Доведемо теорему Остроградського–Гауса: потік електричної індукції через будь-яку замкнену поверхню дорівнює заряду, який є в об’ємі, обмеженому цією поверхнею, тобто
Поиск по сайту: |
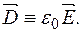
 Потік електричної індукції однорідного електричного поля через плоску поверхню –це скалярний добуток вектора електричної індукції на площу цієї поверхні (позначення
Потік електричної індукції однорідного електричного поля через плоску поверхню –це скалярний добуток вектора електричної індукції на площу цієї поверхні (позначення 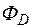 )
)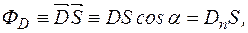
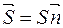 , де
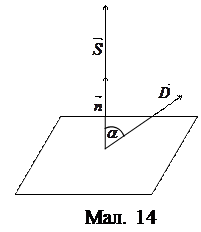
, де 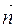 – одиничний вектор нормалі до поверхні (мал. 14).
– одиничний вектор нормалі до поверхні (мал. 14). (19) На основі означення потоку електричної індукції однорідного поля через плоску поверхню виведемо формулу для потоку електричної індукції будь-якого поля через будь яку поверхню.
(19) На основі означення потоку електричної індукції однорідного поля через плоску поверхню виведемо формулу для потоку електричної індукції будь-якого поля через будь яку поверхню.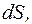 які, очевидно, можна вважати плоскими (мал. 15).
які, очевидно, можна вважати плоскими (мал. 15).
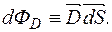
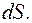 Тому
Тому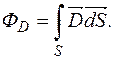
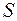 дорівнює сумі площ складових поверхонь, то потік через цю поверхню дорівнює сумі потоків через ці складові поверхні:
дорівнює сумі площ складових поверхонь, то потік через цю поверхню дорівнює сумі потоків через ці складові поверхні: 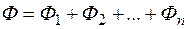 (мал. 16).
(мал. 16).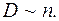
 і
і 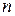 та означенням густоти силових ліній, маємо:
та означенням густоти силових ліній, маємо:
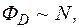
 (1)
(1)