 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Тема 8. Потенціял електростатичного поля
Фізичні величини · Потенціял електростатичного поля в певній точці простору –це відношення роботи, яку слід виконати при переміщенні точкового заряду з цієї точки у нескінченність до величини цього заряду (позначення
Але згадана робота є потенціяльною енергією цієї точки поля
· Різниця потенціялів –різниця між потенціялами двох точок поля (позначення
Задачі (31) Покажемо, що якщо в заданій точці простору є не одне, а багато полів, то потенціял в цій точці дорівнюватиме сумі потенціялів, створених кожним із полів. Згідно з принципом суперпозиції полів, можемо вважати, що в цій точці простору присутнє лише одне поле, яке має відповідні характеристики – напруженість та потенціял. Цей потенціял згідно з означенням
Але роботу А результативного поля можна представити як суму робіт, виконаних окремими полями, тому
Кожен з доданків в останній формулі – це потенціял відповідного поля, тобто
Отже, потенціял в певній точці дорівнює сумі потенціялів, створених кожним із полів:
(32)На основі означення потенціялу встановимо вираз для потенціялу поля точкового заряду Спочатку обчислимо роботу, яку виконує сила поля (чи зовнішня сила проти поля) при переміщенні пробного заряду
Згідно з означенням потенціялу
Потенціяли поля зарядів
та
де
Для точкового диполя потенціял можна виразити через кут
(34)Знайдемо метод обчислення потенціялу, створеного будь-яким неточковим зарядженим тілом.
Для того, щоб обчислити потенціял, створений усім тілом, слід, опираючись на принцип додавання потенціялів, додати всі потенціяли, створені окремими зарядами
Проте інтегрувати за зарядами важко, тому перейдемо до інтегрування за об’ємом, представивши
(35)Знайдемо вираз для потенціялу поля, створеного рівномірно зарядженим диском у будь-якій точці на його осі.
Застосувавши принцип додавання потенціялів, та виразивши заряд через його поверхневу густину, потенціял, створений диском, представимо
Вибираємо довільний елемент площі
Відстань
Поиск по сайту: |
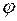 ):
):
 тому потенціял можна записати і так:
тому потенціял можна записати і так:
 ):
):



 в точці, яка є на відстані
в точці, яка є на відстані  від цього заряду.
від цього заряду.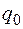 з заданої точки в нескінченність. Оскільки сила зменшується під час переміщення (бо це сила кулонівської взаємодії між зарядами
з заданої точки в нескінченність. Оскільки сила зменшується під час переміщення (бо це сила кулонівської взаємодії між зарядами 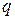 та
та 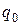 ), то застосуємо формулу роботи змінної сили:
), то застосуємо формулу роботи змінної сили:
 де
де  , бо
, бо  це кут між векторами
це кут між векторами  і
і 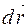 (мал. 26).
(мал. 26).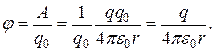
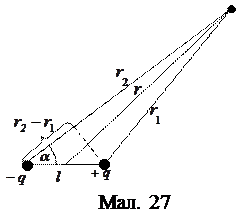 (33) На основі принципу додавання потенціялів та виразу для потенціялу поля точкового заряду встановимо вираз для потенціялу поля точкового диполя.
(33) На основі принципу додавання потенціялів та виразу для потенціялу поля точкового заряду встановимо вираз для потенціялу поля точкового диполя. та
та  відповідно є:
відповідно є:

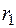 і
і  – відстані від відповідних зарядів до заданої точки. Тому потенціял поля диполя:
– відстані від відповідних зарядів до заданої точки. Тому потенціял поля диполя:
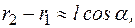
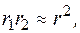 тому вираз для потенціялу поля точкового диполя буде мати вигляд:
тому вираз для потенціялу поля точкового диполя буде мати вигляд:
 Розділимо заряджене тіло на нескінченну кількість нескінченно малих частин і будемо вважати їх точковими зарядами
Розділимо заряджене тіло на нескінченну кількість нескінченно малих частин і будемо вважати їх точковими зарядами 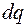 . Тоді потенціял в певній точці на відстані
. Тоді потенціял в певній точці на відстані 
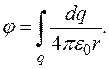
 де
де  – об’ємна густина заряду. Тоді
– об’ємна густина заряду. Тоді
 Розділимо диск на нескінченну кількість малих точкових зарядів
Розділимо диск на нескінченну кількість малих точкових зарядів  Тоді кожен з них в заданій точці Р буде створювати поле з потенціялом
Тоді кожен з них в заданій точці Р буде створювати поле з потенціялом
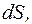 як показано на мал. 29. Тоді
як показано на мал. 29. Тоді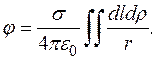
 від елементарної площі до заданої точки представимо через
від елементарної площі до заданої точки представимо через  як
як  а елемент довжини
а елемент довжини 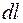 – через кут
– через кут  як
як  . Маємо
. Маємо