 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Тема 16. Потенціяльна енергія взаємодії точкових зарядів. Енергія електричного поля⇐ ПредыдущаяСтр 12 из 12
Фізичні поняття · Потенціяльна енергія заряду в заданій точці електричного поля –це робота, яку слід виконати, щоб перенести цей заряд з цієї точки у нескінченність (позначення Фізичні величини · Об’ємна густина енергії електричного поля –енергія, розрахована на одиницю об’єму зайнятого полем (позначення
Задачі (69)Установимо вираз для потенціяльної енергії взаємодії Спочатку розглянемо систему з двох зарядів. Перший заряд
де замість
Отже, потенціяльна енергія другого заряду в полі першого дорівнює потенціяльній енергії першого заряду в полі другого, тому її ми можемо трактувати як потенціяльну енергію взаємодії двох точкових зарядів. Цю енергію можна подати ще так:
А для системи
(70)Установимо вираз для густини потенціяльної енергії електричного поля. Спочатку зробимо це для однорідного поля (поля плоского конденсатора). Для цього застосуємо послідовно формулу енергії плоского конденсатора, формулу зв’язку напруженості і напруги та формулу для ємності плоского конденсатора. Отримаємо
де
а енергія електричного поля в об’ємі
Діленням передостаннього рівняння на
(71) Установимо вираз для потенціяльної енергії зарядженого провідника та конденсатора. Щоб перенести заряд
або представивши
Щоб перенести весь заряд
яка за означенням потенціяльної енергії і є потенціяльною енергією зарядженого провідника:
або, взявши до уваги означення ємності
Поиск по сайту: |
 ).
).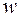 ).
).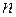 точкових зарядів.
точкових зарядів.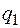 будемо вважати джерелом поля. Тоді потенціяльна енергія другого заряду
будемо вважати джерелом поля. Тоді потенціяльна енергія другого заряду 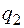 в полі першого, згідно з означенням потенціялу, буде
в полі першого, згідно з означенням потенціялу, буде

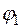 ми підставили відомий вираз для потенціялу поля точкового заряду. З іншого боку, оскільки заряди
ми підставили відомий вираз для потенціялу поля точкового заряду. З іншого боку, оскільки заряди 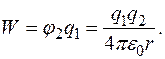
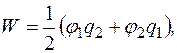
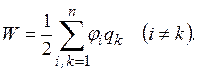
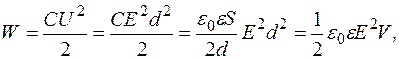
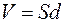 – об’єм конденсатора.
– об’єм конденсатора.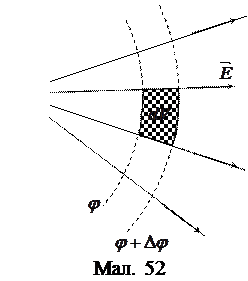 Якщо поле неоднорідне, то виділимо в ньому нескінченно малий об’єм, обмежений двома нескінченно близькими еквіпотенціяльними поверхнями та площинами нормальними до них, які проходять через силові лінії (мал. 52). Такий об’єм можна вважати плоским конденсатором з обкладками на еквіпотенціяльних поверхнях, бо будь-яку еквіпотенціяльну поверхню можна замінити на реальну провідну поверхню з тим самим потенціялом. Енергія цього конденсатора
Якщо поле неоднорідне, то виділимо в ньому нескінченно малий об’єм, обмежений двома нескінченно близькими еквіпотенціяльними поверхнями та площинами нормальними до них, які проходять через силові лінії (мал. 52). Такий об’єм можна вважати плоским конденсатором з обкладками на еквіпотенціяльних поверхнях, бо будь-яку еквіпотенціяльну поверхню можна замінити на реальну провідну поверхню з тим самим потенціялом. Енергія цього конденсатора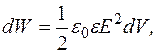

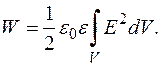
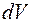 отримаємо формулу для обчислення об’ємної густини енергії
отримаємо формулу для обчислення об’ємної густини енергії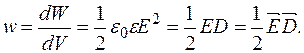
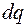 з провідника в нескінченість, слід, згідно з означенням потенціялу, виконати роботу
з провідника в нескінченість, слід, згідно з означенням потенціялу, виконати роботу
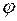 згідно з означенням ємності
згідно з означенням ємності 
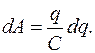
 , слід виконати роботу:
, слід виконати роботу: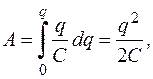
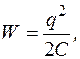 (5)
(5) (6)
(6)