 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Тема 3. Електричне поле і його напруженість
Фізичні поняття · Електричне поле – це субстанція, яка створюється електричними зарядами і виявляє себе за дією на електричний заряд. Як бачимо, заряд є водночас і джерелом поля, і тим інструментом, який виявляє присутність електричного поля. · Пробний заряд – це позитивний точковий заряд, який служить для виявлення та вимірювання електричного поля. Очевидно, що реальний пробний заряд, крім дуже малих розмірів, повинен мати і дуже малу величину, бо інакше, будучи джерелом ще одного поля, він спотворюватиме досліджуване поле. · Лінія напруженості електричного поля (чи силова лінія) – це лінія у кожній точці якої вектор напруженості поля дотичний до цієї лінії, або, інакше, – це лінія, вздовж якої рухається пробний заряд, на який не діють жодні сили, крім сил електричного поля.
Фізичні величини · Напруженість електричного поля в заданій точці простору – це відношення сили, яка діє з боку цього поля на пробний заряд, поміщений в цю точку до величини цього заряду (позначення
З цього означення бачимо, що оскільки сила є вектором, то і напруженість є вектором. Крім того вектор
Задачі
(6) Знайдемо заряд електрона в ході мисленнево проведеного досліду Мілікена (1909 р).
Для цього спочатку виміряємо заряд краплі в звичайному повітрі Щоб виміряти заряд краплі, слід виміряти коефіцієнт опору при русі краплі в повітрі за відомою методикою.
або
звідки знаходимо коефіцієнт опору
Далі зробимо такий самий експеримент, але в електричному полі, напрямленому вниз. Тепер негативно заряджена крапля буде рухатися рівномірно вгору зі швидкістю
З цієї рівності та рівності (1), враховуючи, що
Усі величини в правій частині цієї рівності досить легко вимірюються експериментально. Далі слід йонізувати простір між пластинами якимось йонізатором, наприклад, Х-променями, провести такий самий експеримент і знову за тією ж формулою обчислити заряд
де
(7) На основі означення напруженості електричного поля та закону Кулона установимо вираз для напруженості поля точкового заряду. Нехай поле створене точковим зарядом
Отже,
або
а величина напруженості
(8) Установимо картину силових ліній поля точкового заряду.
де
(9) Покажемо, що густота ліній напруженості електричного поля точкового заряду в певній області простору вказує на величину напруженості електричного поля в цій області. З виразу для напруженості поля точкового заряду випливає, що вона залежить лише від відстані від заряду, тобто є всюди однакова на сфері радіусом
де Густота силових ліній – це кількість силових ліній на одиницю площі поверхні, нормальної до цих силових ліній
Підставивши
звідки бачимо, що величина напруженості пропорційна до густоти силових ліній Зауважимо, що для випадку поля точкового заряду цей висновок не має значної цінності, бо з аналітичного виразу і так видно, що ближче до заряду, то сильніше поле. Проте в тих випадках, де немає аналітичного виразу для величини вектора
Поиск по сайту: |
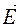 )
)

 Ідея досліду Мілікена полягає в тому, щоб знайти зміну заряду попередньо зарядженої краплі оливи в йонізованому повітрі.
Ідея досліду Мілікена полягає в тому, щоб знайти зміну заряду попередньо зарядженої краплі оливи в йонізованому повітрі. , а потім – в йонізованому
, а потім – в йонізованому 
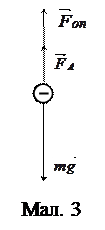
 На краплю, яка падає у повітрі, діють три сили: сила тяжіння
На краплю, яка падає у повітрі, діють три сили: сила тяжіння 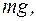 сила Архімеда
сила Архімеда  та сила опору повітря
та сила опору повітря  , де
, де  – коефіцієнт опору (мал. 3). Дві перші з цих сил постійні і лише третя зростає зі збільшенням швидкості, тому в міру її збільшення буде зростати і сила опору. Через певний час після початку падіння ця сила разом із силою Архімеда, які діють вгору, зрівноважать силу тяжіння і рух перейде в рівномірний
– коефіцієнт опору (мал. 3). Дві перші з цих сил постійні і лише третя зростає зі збільшенням швидкості, тому в міру її збільшення буде зростати і сила опору. Через певний час після початку падіння ця сила разом із силою Архімеда, які діють вгору, зрівноважать силу тяжіння і рух перейде в рівномірний

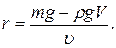 (1)
(1) (мал. 4). Напишемо основне рівняння динаміки і для цього випадку
(мал. 4). Напишемо основне рівняння динаміки і для цього випадку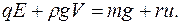
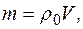 де
де 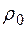 – густина оливи, дістанемо
– густина оливи, дістанемо
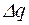 становить ціле число зарядів
становить ціле число зарядів 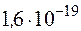 Кл, тобто
Кл, тобто
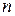 – ціле число.
– ціле число. Якщо в це поле внести пробний заряд
Якщо в це поле внести пробний заряд 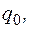 то на нього з боку поля діятиме сила
то на нього з боку поля діятиме сила  Але ця сила – це сила кулонівської взаємодії між зарядами
Але ця сила – це сила кулонівської взаємодії між зарядами 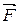 вираз цього закону
вираз цього закону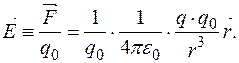
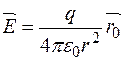
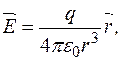
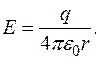
 Нехай цей заряд позитивний. Розмістимо будь - де пробний заряд
Нехай цей заряд позитивний. Розмістимо будь - де пробний заряд 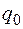 (мал. 5). Напруженість поля в цій точці
(мал. 5). Напруженість поля в цій точці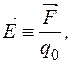
 – сила, яка діє з боку поля заряду
– сила, яка діє з боку поля заряду 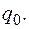 Але
Але  Такий самий результат буде в будь-якій іншій точці простору. Отже, поле точкового заряду радіальне.
Такий самий результат буде в будь-якій іншій точці простору. Отже, поле точкового заряду радіальне. Представимо цей вираз так:
Представимо цей вираз так: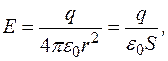
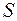 – площа сфери радіусом
– площа сфери радіусом 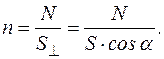
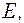 дістанемо
дістанемо
 тобто, там де більша густота силових ліній, там і більша напруженість поля.
тобто, там де більша густота силових ліній, там і більша напруженість поля. цей метод дає можливість на основі графічної картини силових ліній порівняти напруженість поля в різних областях цього поля.
цей метод дає можливість на основі графічної картини силових ліній порівняти напруженість поля в різних областях цього поля.