 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Тема 10. Зв'язок між напруженістю і потенціялом
Фізичні поняття · Градієнт даної скалярної величини
· Еквіпотенціяльна поверхня –поверхня, у кожній точці якої потенціял однаковий.
Задачі (39)Установимо зв'язок між напруженістю електростатичного поля та його потенціялом. Згідно з означеннями потенціялу та роботи
де знак «–», який з’явився при заміні Знайдемо частинну похідну від
Оскільки
Аналогічно
та
Але вектор
Взявши до уваги рівності (1), (2), (3), дістанемо
З цієї формули бачимо, що оскільки вектор
(40) З формули зв’язку напруженості і потенціялу та теореми Остроградського–Гауса отримаємо рівняння Пуассона. Підставимо формулу зв’язку між напруженістю та потенціялом у формулу, яка виражає теорему Остроградського–Гауса в диферентціяльній формі
або
або скорочено
де Останнє рівняння називають рівняннями Пуассона. За умови
(41) Доведемо, що вектор напруженості електростатичного поля завжди нормальний до еквіпотенціяльної поверхні. Виберемо систему координат так, щоб вектори
(Пам’ятаємо, що похідна в будь-якій точці – це кутовий коефіцієнт дотичної в цій точці, а оскільки цей кутовий коефіцієнт дорівнює нулеві, то і похідна дорівнює нулеві). Тому, згідно з формулою зв’язку напруженості і потенціялу
що означає, що
(42) Доведемо теорему про середнє значення потенціялу: потенціял у будь-якій точці простору дорівнює середньому значенню потенціялу на будь-якій уявній сфері з центром в цій точці, яка не охоплює електричних зарядів. Напишемо формулу для середнього значення потенціялу на сфері
і знайдемо похідну від
Згідно з формулою зв’язку між напруженістю і потенціялом
а за теоремою Остроградського–Гауса, оскільки в області обмеженій сферою електричні заряди відсутні, останній вираз дорівнює нулеві. Отже,
що означає, що
(43) Пояснимо метод електростатичного очищення газів.
Цей провід перебуває під високою негативною напругою. Оскільки поблизу проводу висока напруженість поля (велика густота силових ліній), то повітря йонізується і потік електронів та йонів Ці негативно наелектризовані частинки починають рухатися проти поля і прилипають до стінок. Тоді їх струшують на дно бочки.
Поиск по сайту: |
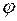 –це вектор, спрямований у бік найбільшого зростання цієї фізичної величини, модуль якого дорівнює відношенню зміни цієї фізичної величини до відстані в цьому напрямі найбільшого зростання, на якій відбулася ця зміна (позначення
–це вектор, спрямований у бік найбільшого зростання цієї фізичної величини, модуль якого дорівнює відношенню зміни цієї фізичної величини до відстані в цьому напрямі найбільшого зростання, на якій відбулася ця зміна (позначення  ):
):

 на
на  вказує на те, що вектор
вказує на те, що вектор 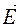 є протилежним до вектора зовнішньої сили
є протилежним до вектора зовнішньої сили 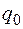 позитивний).
позитивний).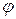 за
за 

 та
та  отримаємо що
отримаємо що (1)
(1) , (2)
, (2) (3)
(3) як і будь-який інший, можна подати як лінійну комбінацію одиничних векторів
як і будь-який інший, можна подати як лінійну комбінацію одиничних векторів

 Дістанемо
Дістанемо

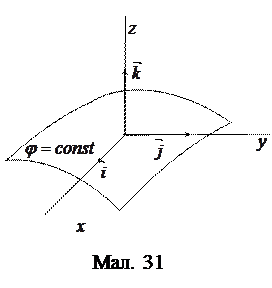 Оскільки операція дивергенції полягає в тому, що слід взяти похідні за
Оскільки операція дивергенції полягає в тому, що слід взяти похідні за  і
і  від компонентів вектора і додати їх, то остання рівність набуває вигляду
від компонентів вектора і додати їх, то остання рівність набуває вигляду

 – оператор Лапласа.
– оператор Лапласа. це рівняння називають рівнянням Лапласа:
це рівняння називають рівнянням Лапласа: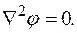
 та
та  були дотичні до еквіпотенціяльної поверхні (мал. 31). Тоді в цій точці дотику
були дотичні до еквіпотенціяльної поверхні (мал. 31). Тоді в цій точці дотику і
і 
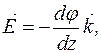
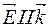 , тобто вектор
, тобто вектор 
 за радіусом сфери
за радіусом сфери 

 це проекція вектора напруженості на радіус
це проекція вектора напруженості на радіус  , тому
, тому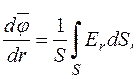


 Для очищення газів беруть велику металеву бочку з провідником у її центрі, який ізольований від самої бочки (мал. 32).
Для очищення газів беруть велику металеву бочку з провідником у її центрі, який ізольований від самої бочки (мал. 32).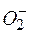 електризує частинки домішок, які є в забрудненому газі, негативним зарядом.
електризує частинки домішок, які є в забрудненому газі, негативним зарядом.