 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Тема 7. Обчислення напруженостей електричних полів на основі теореми Остроградського–Гауса
Задачі (23) На основі теореми Остроградського–Гауса встановимо вираз для напруженості електричного поля точкового заряду.
Згідно з теоремою Остроградського–Гауса, прирівняємо отриманий результат до величини заряду
звідки
А для вектора
(24)На основі теореми Остроградського–Гауса встановимо вираз для напруженості електричного поля рівномірно зарядженої площини з поверхневою густиною заряду
Охопимо частину площини паралелепіпедом, поверхня якого проходить через задану точку (мал. 21) і знайдемо потік через його поверхню. Очевидно, що потоки через грані, нормальні до площини, дорівнюють нулеві, бо кут
звідки:
і
Зауважте, що напруженість поля нескінченної площини – це стала величина, яка не залежить від відстані від площини. Якщо площина обмежена, то очевидно ця формула правильна тільки для точок розміщених дуже близько до неї.
(25) На основі теореми Остроградського–Гауса встановимо вираз для напруженості електричного поля на поверхні зарядженого провідника. Для розв’язання цієї задачі скористаємося тим фактом, що електричне поле всередині провідника відсутнє (надалі ми поставимо перед собою задачу довести це). Очевидно, що для всіх точок, які лежать дуже близько до поверхні провідника, провідник можна вважати нескінченною площиною, якої б форми він не був. Отже, задача зводиться до попередньої з тією різницею, що поле існує лише поза провідником (мал. 21). За теоремою Остроградського–Гауса
звідки
З міркувань симетрії, подібних до міркувань щодо поля не скінченної площини, знаходимо, що вектор електричної індукції у будь-якій точці є нормальним до нитки (мал. 22, а, б). Охопимо частину нитки уявним циліндром поверхня якого проходить через точку в якій ми шукаємо напруженість поля. Знайдемо потік електричної індукції через цей циліндр. З малюнка видно, що потік через основи циліндра дорівнює нулеві, бо кут між векторами Потік через бічну поверхню
Всередині циліндра знаходиться заряд
тому за теоремою Остроградського–Гауса
звідки
і
(27)На основі теореми Остроградського-Гауса встановимо вираз для напруженості електричного поля рівномірно зарядженої сфери.
Нехай на сфері є сумарний заряд
Бачимо, що напруженість поля сфери з зарядом
(28) На основі теореми Остроградського–Гауса встановимо вираз для напруженості електричного поля рівномірно зарядженого не скінчено довгого циліндра.
Оскільки всюди на поверхні уявного циліндра поле однакове за величиною і спрямоване вздовж нормалі до циліндра, то потік матиме найпростіший вигляд
або
де З малюнка бачимо, що потік через основи циліндра дорівнює нулеві, тому остання формула набуває вигляду:
звідки
(29) Доведемо, що в об’ємі, обмеженому зарядженою поверхнею, напруженість електричного поля дорівнює нулеві.
Проведемо всередині поверхні уявну поверхню нескінченно близько до зарядженої поверхні (мал. 25). У цьому об’ємі немає зарядів, тому згідно з теоремою Остроградського–Гауса
звідки:
і
(30) З’ясуємо, для розрахунку яких електричних полів можна ефективно застосовувати теорему Остроградського–Гауса. По-перше, очевидним є те, що нам має бути відома графічна картина силових ліній цього поля. По-друге, оскільки індукція (чи напруженість) електричного поля входить у вираз для потоку, то в загальному випадку вона є під знаком визначеного інтеграла в підінтегральному виразі. Для того, щоб проінтегрувати, слід встановити залежності всіх величин (букв) підінтегрального виразу від змінної інтегрування і винести за знак інтеграла ті величини, які від неї не залежать. Стосовно вектора електричної індукції, це означає, що якщо він залежить від змінної інтегрування
Поиск по сайту: |
 Охопимо заряд уявною сферичною поверхнею, яка проходить через точку, в якій ми шукаємо напруженість поля. Знайдемо потік електричної індукції через цю поверхню.
Охопимо заряд уявною сферичною поверхнею, яка проходить через точку, в якій ми шукаємо напруженість поля. Знайдемо потік електричної індукції через цю поверхню.







 Спочатку встановимо напрям вектора
Спочатку встановимо напрям вектора  в довільній заданій точці простору, тобто з’ясуємо картину силових ліній поля. Згідно з принципом суперпозиції електричних полів, вектор
в довільній заданій точці простору, тобто з’ясуємо картину силових ліній поля. Згідно з принципом суперпозиції електричних полів, вектор  створених нескінченно малими ділянками площини. Оскільки площина нескінченна, то для будь-якого електричного заряду
створених нескінченно малими ділянками площини. Оскільки площина нескінченна, то для будь-якого електричного заряду 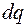 знайдеться симетричний, який дає протилежну проекцію на горизонтальну вісь (мал. 20). Отже, всі горизонтальні проекції будуть скомпенсовані, залишаться тільки вертикальні, що означає, що лінії індукції електричного поля це прямі паралельні до площини.
знайдеться симетричний, який дає протилежну проекцію на горизонтальну вісь (мал. 20). Отже, всі горизонтальні проекції будуть скомпенсовані, залишаться тільки вертикальні, що означає, що лінії індукції електричного поля це прямі паралельні до площини. між вектором
між вектором  Залишаються потоки через грані, паралельні до площини. Згідно з теоремою Остроградського–Гауса, враховуючи, що поле однорідне всюди на грані, маємо:
Залишаються потоки через грані, паралельні до площини. Згідно з теоремою Остроградського–Гауса, враховуючи, що поле однорідне всюди на грані, маємо:
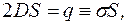





 (26)На основі теореми Остроградського–Гауса встановимо вираз для напруженості електричного поля рівномірно зарядженої нескінченно довгої прямої нитки з лінійною густиною заряду
(26)На основі теореми Остроградського–Гауса встановимо вираз для напруженості електричного поля рівномірно зарядженої нескінченно довгої прямої нитки з лінійною густиною заряду 
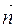 прямий.
прямий.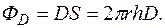
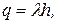
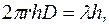
 ,
,
 З міркувань симетрії робимо висновок, що вектор
З міркувань симетрії робимо висновок, що вектор 
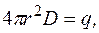
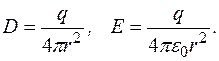
 Охопимо заряджений циліндр ще одним уявним циліндром, проте таким, який проходить через точку, в якій ми шукаємо напруженість поля. З тих же міркувань, що і для поля нитки, робимо висновок, що лінії напруженості є прямі нормальні до бічної поверхні циліндра (мал. 24, а, б).
Охопимо заряджений циліндр ще одним уявним циліндром, проте таким, який проходить через точку, в якій ми шукаємо напруженість поля. З тих же міркувань, що і для поля нитки, робимо висновок, що лінії напруженості є прямі нормальні до бічної поверхні циліндра (мал. 24, а, б).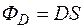 і згідно з теоремою Остроградського–Гауса
і згідно з теоремою Остроградського–Гауса
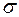 – поверхнева густина заряду на циліндрі,
– поверхнева густина заряду на циліндрі,  – площа бічної поверхні реального циліндра.
– площа бічної поверхні реального циліндра.



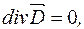
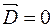
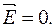
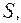 то, встановивши цю залежність, ми втратимо цю величину (букву
то, встановивши цю залежність, ми втратимо цю величину (букву  , а щоб вона збереглася у виразі потоку, то має бути незалежною від змінної інтегрування
, а щоб вона збереглася у виразі потоку, то має бути незалежною від змінної інтегрування 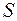 . Таким чином, робимо висновок, що теорему Остроградського–Гауса варто застосовувати до тих полів, для яких ми можемо віднайти таку уявну замкнену поверхню, на якій величина
. Таким чином, робимо висновок, що теорему Остроградського–Гауса варто застосовувати до тих полів, для яких ми можемо віднайти таку уявну замкнену поверхню, на якій величина  є всюди однакова.
є всюди однакова.