 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Тема 14. Електроємність
Фізичні величини · Електроємність відокремленого провідника –це відношення зміни заряду провідника до зміни його потенціялу, яка спричинена цією зміною заряду (позначення С).
Якщо провідник був незаряджений, то його ємність очевидно означається так
Фізичні системи й прилади · Конденсатор –система двох електрично ізольованих один від одного провідників.
Задачі (59) Покажемо, що потенціял відокремленого провідника пропорційний до його заряду. Відомо, що будь-який провідник, заряджений чи ні, є еквіпотенціяльний, що означає, що потенціял у всіх його точках однаковий (задача 46). Крім того відомо, що заряд розміщується лише на поверхні провідника (задача 44). На основі принципу додавання потенціялів, потенціял у будь-якій точці провідника буде дорівнювати сумі потенціялів, створених елементами заряду
де Але поверхнева густина заряду пропорційна до величини заряду
Оскільки вираз
(60) Покажемо: якщо поблизу провідника розмістити інший провідник, то його ємність збільшиться. На мал. 43, (а) показано відокремлений заряджений провідник і його поле. Якщо поблизу цього провідника розмістити інший незаряджений провідник, то внаслідок виникнення на ньому індукованого заряду поле між провідниками підсилюється, а за ними послаблюється, тому заряд на першому провіднику перерозподілиться (мал. 43, (б)). Щодо потенціялу в будь-якій точці першого провідника (пам’ятаємо, що він всюди однаковий), то бачимо, що згідно з принципом додавання потенціялів, його алгебраїчна сума зменшиться і ємність згідно з її означенням зросте. Очевидно, що цей ефект збільшення ємності провідника під впливом іншого провідника буде тим більший, що ближче будуть один до одного ці провідники і що більші їхні площі будуть розташовані одні навпроти одних. Оскільки така система двох провідників – це конденсатор, то бачимо, що ємність конденсатора може бути значно більшою за ємність відокремленого провідника.
(61)Установимо вираз для електроємності провідної кулі та сфери і обчислимо ємність Землі. Якщо кулі надати заряду
Згідно з означенням ємності
Щодо сфери, то заряд на сфері розміститься так само, як і на кулі і потенціял всередині сфери буде такий самий, як і всередині кулі, тому ємність сфери така ж, як і ємність кулі такого ж радіуса. Якщо сфера заповнена діелектриком з діелектричною проникністю
За цією формулою ємність Земної кулі
Тема 15. Конденсатори Задачі (62)Установимо вираз для ємності плоского конденсатора.
де
де
(63) Установимо вираз для ємності циліндричного конденсатора довжина якого значно більша за радіуси циліндрів.
З формули зв’язку напруженості і потенціялу знайдемо потенціял у цій же точці:
звідки
Сталу інтегрування К знайдемо з умови
звідки потенціял зовнішнього циліндра щодо внутрішнього:
Тепер можемо написати і вираз для ємності:
Очевидно, що ця формула правильна і для коаксіального кабеля. Розглянемо випадок коли відстань між циліндрами Скориставшись з наближеної формули для обчислення логаритма, а саме, що за близьких значень
Врахувавши те, що
як і для плоского конденсатора.
(64)Доведемо, що за паралельного з’єднання двох чи більше конденсаторів ємність цієї ділянки кола дорівнює сумі ємностей окремих конденсаторів. Будемо розглядати цю ділянку кола як один великий конденсатор з двома ізольованими один від одного провідниками А і В (ці провідники обведені на мал. 46 замкнутими штрихованими лініями).
де
За більшої кількості конденсаторів нічого не зміниться, тому
(65)Покажемо, що ємність конденсатора будь-якої форми за умови, що відстань між його обкладками є значно меншою за їхні розміри, дорівнює ємності плоского конденсатора з такою ж площею обкладок і відстанню між ними.
За паралельного з’єднання ємності додаються, тому
Якщо в цьому випадку одному конденсатору надати заряду За означенням ємності, ємність батареї
За тим самим означенням ємності
і тоді
звідки маємо
(67)Установимо вираз для ємності двохпровідної лінії, тобто системи двох паралельних проводів довжиною
Підставивши в останню рівність вираз для поверхневої густини заряду на циліндрі
Другий провід, очевидно, створює у цій точці напруженість поля
Тому сумарна напруженість поля в цій точці
Підставивши у цей вираз
звідки інтегруванням установимо залежність потенціялу від відстані
Сталу К знайдемо з умови
Маючи цю залежність можемо визначити потенціял
Оскільки потенціял першого проводу ми прийняли за нуль, то ця величина є різницею потенціалів між проводами, тому згідно з означенням ємності
Ємність, що припадає на одиницю довжини лінії
(68)Установимо вираз для ємності однопровідної лінії довжиною Застосуємо метод дзеркальних зображень. Згідно з цим методом, електричне поле, створене зарядженим проводом та індукованим зарядом на поверхні землі, співпадає з електричним полем, створеним двома проводами з однаковими за величиною та протилежними за знаками зарядами (мал. 50).
Але нас цікавить різниця потенціялів між проводом та землею і вона, очевидно, дорівнює половині різниці потенціялів між проводом і його зображенням. Тоді, врахувавши це за означенням ємності,
Ємність одиниці довжини проводу:
Поиск по сайту: |
 (1)
(1) (2)
(2)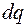 :
:
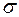 – поверхнева густина заряду на провіднику,
– поверхнева густина заряду на провіднику, 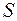 – площа поверхні провідника.
– площа поверхні провідника. , тобто
, тобто  або
або  , де
, де  – коефіцієнт, який не обов’язково є сталим, а може і залежати від
– коефіцієнт, який не обов’язково є сталим, а може і залежати від 
 – це число, то
– це число, то 

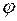 , причому він буде однаковий в усіх точках кулі (задача 45). Найлегше нам знайти потенціял у центрі кулі. Оскільки заряд розміститься на поверхні кулі (задача 44), то потенціял у її центрі створюється зарядом її поверхні. Кожен елементарний заряд поверхні
, причому він буде однаковий в усіх точках кулі (задача 45). Найлегше нам знайти потенціял у центрі кулі. Оскільки заряд розміститься на поверхні кулі (задача 44), то потенціял у її центрі створюється зарядом її поверхні. Кожен елементарний заряд поверхні  , де
, де  – радіус кулі, а весь заряд кулі створює потенціял
– радіус кулі, а весь заряд кулі створює потенціял

 , то очевидно її ємність:
, то очевидно її ємність:

 Згідно з означенням ємності
Згідно з означенням ємності
 – різниця потенціалів між обкладками конденсатора (мал.. 44), яка за формулою зв’язку між напруженістю і потенціялом може бути представлена як
– різниця потенціалів між обкладками конденсатора (мал.. 44), яка за формулою зв’язку між напруженістю і потенціялом може бути представлена як  Своєю чергою напруженість електричного поля
Своєю чергою напруженість електричного поля  між обкладками конденсатора дорівнює
між обкладками конденсатора дорівнює  як напруженість поля двох нескінченних площин. Отже
як напруженість поля двох нескінченних площин. Отже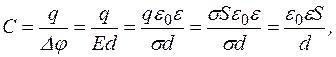
 Спочатку встановимо вираз для потенціялу будь-якої точки між двома циліндрами (мал. 45). Для цього встановимо вираз для напруженості поля. Напруженість поля в цій точці, створена зовнішнім циліндром згідно з теоремою Остроградського–Гауса дорівнює нулеві, бо потік напруженості електричного поля зовнішнього циліндра дорівнює нулеві тому, що під цією поверхнею немає електричних зарядів. У результаті напруженість поля між циліндрами – це напруженість, створена внутрішнім циліндром, і за тією ж теоремою Остроградського –Гауса (задача 28)
Спочатку встановимо вираз для потенціялу будь-якої точки між двома циліндрами (мал. 45). Для цього встановимо вираз для напруженості поля. Напруженість поля в цій точці, створена зовнішнім циліндром згідно з теоремою Остроградського–Гауса дорівнює нулеві, бо потік напруженості електричного поля зовнішнього циліндра дорівнює нулеві тому, що під цією поверхнею немає електричних зарядів. У результаті напруженість поля між циліндрами – це напруженість, створена внутрішнім циліндром, і за тією ж теоремою Остроградського –Гауса (задача 28)



 тобто приймаємо потенціял одного з циліндрів, а саме зовнішнього за нуль. Після підстановки маємо
тобто приймаємо потенціял одного з циліндрів, а саме зовнішнього за нуль. Після підстановки маємо  і вираз для потенціялу набирає вигляду:
і вираз для потенціялу набирає вигляду:


 значно менша за їхні радіуси.
значно менша за їхні радіуси.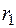 і
і  :
:  матимемо
матимемо
 це площа
це площа  остаточно маємо:
остаточно маємо:
 Згідно з означенням ємності, ємність цього конденсатора:
Згідно з означенням ємності, ємність цього конденсатора: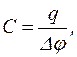
 і
і  дістанемо:
дістанемо:

 Уявімо конденсатор будь-якої форми як систему паралельно з’єднаних плоских елементарних конденсаторів з площею обкладок
Уявімо конденсатор будь-якої форми як систему паралельно з’єднаних плоских елементарних конденсаторів з площею обкладок 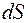 (мал. 47). Оскільки відстань між обкладками мала, поле в межах одного елементарного конденсатора можна вважати однорідним. Тому ємність кожного елементарного конденсатора
(мал. 47). Оскільки відстань між обкладками мала, поле в межах одного елементарного конденсатора можна вважати однорідним. Тому ємність кожного елементарного конденсатора  – це ємність плоского конденсатора
– це ємність плоского конденсатора

 (66)Доведемо, що за послідовного з’єднання двох чи більше конденсаторів обернена ємність цієї ділянки кола дорівнює сумі обернених ємностей окремих конденсаторів.
(66)Доведемо, що за послідовного з’єднання двох чи більше конденсаторів обернена ємність цієї ділянки кола дорівнює сумі обернених ємностей окремих конденсаторів. та
та  (поля зарядів усіх інших обкладок компенсують одне одного).
(поля зарядів усіх інших обкладок компенсують одне одного).



 радіусами
радіусами  відстань між осями яких
відстань між осями яких  причому розглянемо практичний випадок коли
причому розглянемо практичний випадок коли  .
. Спочатку знайдемо вираз для напруженості електричного поля, створеного одним з проводів у будь-якій точці на прямій, що з’єднує два проводи, що на відстані х від одного з них (мал. 49). Для цього скористаємося виразом для напруженості поля рівномірно зарядженого циліндра (задача 27) (зауважимо, що практична рівномірність розподілу заряду на проводі забезпечується умовою
Спочатку знайдемо вираз для напруженості електричного поля, створеного одним з проводів у будь-якій точці на прямій, що з’єднує два проводи, що на відстані х від одного з них (мал. 49). Для цього скористаємося виразом для напруженості поля рівномірно зарядженого циліндра (задача 27) (зауважимо, що практична рівномірність розподілу заряду на проводі забезпечується умовою 
 де
де 

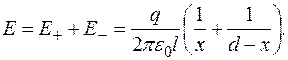
 дістанемо
дістанемо
 :
:

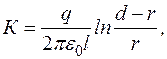 а після підстановки цього виразу в отриману залежність
а після підстановки цього виразу в отриману залежність  :
:




 над землею.
над землею. Тому застосуємо вираз для різниці потенціялів між двома проводами (задача 67):
Тому застосуємо вираз для різниці потенціялів між двома проводами (задача 67):

