 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Тема 4. Принцип суперпозиції електричних полів
Постулати Ø Принцип суперпозиції електричних полів: система точкових зарядів створює у кожній точці простору поле, напруженість якого дорівнює сумі напруженостей, створених кожним із цих зарядів
Задачі (10) Вкажемо на метод знаходження напруженості електричного поля зарядженого тіла, яке не можна вважати точковим зарядом. Будь-яке заряджене тіло представимо як систему нескінченної кількості нескінченно близьких один до одного, нескінченно малих точкових зарядів величиною
Згідно з принципом суперпозиції, напруженість електричного поля у цій точці буде дорівнювати сумі згаданих напруженостей. Очевидно, що ми маємо справу з сумою нескінченної кількості нескінченно малих величин. А це є не що інше, як інтеграл. Отже,
З цієї формули бачимо, що інтегрування слід провести по всьому заряду тіла, що важко зробити практично. Тому від інтегрування за зарядом перейдемо до інтегрування за об’ємом. Для цього застосуємо поняття об’ємної густини заряду
тобто, принципово ми можемо обчислити напруженість поля, створену будь яким зарядженим тілом.
(11) Установимо вираз для напруженості електричного поля рівномірно зарядженого кільця радіусом
Тоді:
З малюнка бачимо, що для кожного вектора
Задача спростилася і
Як видно з малюнка
тому
Враховуючи, що
Отже, інтегрування буде йти по всій довжині кільця Щоб обчислити цей інтеграл, слід кожну величину у підінтегральному виразі подати через змінну інтегрування
Представимо тепер всі ці величини через відомі
І для вектора
Остання рівність говорить про те, що шукана нами напруженість електричного поля – це вектор, спрямований вздовж осі у, величина якого
або оскільки кільце рівномірно заряджене, замінивши
Розділимо диск на нескінченну кількість кілець і скористаємося результатом попередньої задачі. Одне з таких кілець товщиною
Зверніть увагу, що замість сталого радіуса кільця Виразимо
де
Інтегруємо
Остаточно,
(13) Знайдемо середнє значення напруженості електричного поля точкового заряду в межах майданчика у вигляді диска, якщо заряд є на осі цього диска. Математичний відступ: середнє значення функції.
або представивши
При
Повернемося до нашої задачі (мал. 9). З міркувань симетрії можемо зробити висновок, що середнє значення напруженості поля вздовж будь-якого радіуса диска однакове і тому дорівнює середньому значенню на всьому диску. Отже, нам досить обчислити середнє значення вздовж будь-якого радіуса
Остаточно,
Тема 5. Диполь Фізичні поняття · Плече диполя –вектор, проведений від негативного заряду диполя до позитивного (позначення · Жорсткий диполь –диполь, плече якого залишається сталим. · Точковий диполь –диполь, плече якого значно менше за відстань від диполя до точки спостереження.
Фізичні величини · Дипольний момент –це добуток одного із зарядів диполя на його плече (позначення
Фізичні системи й прилади · Диполь –це система двох однакових за величиною та протилежних за знаком точкових зарядів. Задачі
Під вільним диполем очевидно розуміємо вільне тіло, тобто тіло, на яке не діють жодні сили. На кожен із зарядів диполя діє сила величиною
величина якого
де
(15)Установимо вираз для напруженості електричного поля точкового диполя з плечем Згідно з принципом суперпозиції електричних полів (мал. 11)
де
де знак «–» вказує на те, що відповідний заряд негативний і вектори Виразимо вектори
а також довжини векторів
звідки
Повертаючись до рівності (1) і підставляючи в неї (2), (3) і (4), матимемо
Піднявши вирази в знаменниках до кубу й знехтувавши доданками, які містять малі порівняно з одиницею величини
Звівши до спільного знаменника, який буде
Після перетворень і врахувавши, що
або, врахувавши, що
Знайдемо ще вираз для модуля вектора
Після перетворення дістанемо
Формули (4) і (5) задають напрям і величину вектора
(16) Покажемо, що в неоднорідному електричному полі вільний диполь не буде в стані спокою (на відміну від випадку однорідного поля, де диполь є в стані спокою), а рухатиметься в напрямі зростання поля. Очевидно, що як тільки диполь потрапить в електричне поле, він розташується вздовж однієї із його силових ліній так, що його дипольний момент буде паралельний до неї (мал. 12).
де
Отже, рівнодійна сила, яка діє на диполь, не дорівнює нулеві, і диполь буде рухатися у напрямку зростання поля.
(17)Пояснимо явище притягання дрібних частинок до наелектризованих тіл. Наприклад, це можуть бути шматочки паперу, які притягаються до наелектризованої пластмасової кулькової ручки або пил до екрана телевізора. В електричному полі наелектризованого тіла маленькі частинки стають диполями (поляризуються), а оскільки це поле неоднорідне, то як ми вже з’ясували, то вони рухаються у бік його зростання, тобто до тіла.
(18) Пояснимо принцип роботи йонного мікроскопа.
Поиск по сайту: |

 Очевидно, що кожен з цих зарядів буде створювати в певній точці простору нескінченно мале електричне поле напруженістю:
Очевидно, що кожен з цих зарядів буде створювати в певній точці простору нескінченно мале електричне поле напруженістю:

 Дістанемо
Дістанемо
 і лінійною густиною заряду
і лінійною густиною заряду  на осі кільця на відстані
на осі кільця на відстані  від його центру.
від його центру. Згідно з принципом суперпозиції
Згідно з принципом суперпозиції 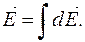 Розкладемо вектор
Розкладемо вектор 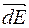 на дві складові (мал. 6):
на дві складові (мал. 6):

 знайдеться до нього протилежний і таким чином сума всіх х–ових складових вектора
знайдеться до нього протилежний і таким чином сума всіх х–ових складових вектора  дорівнює нулеві, тобто
дорівнює нулеві, тобто



 де
де 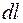 – елемент довжини кільця, маємо
– елемент довжини кільця, маємо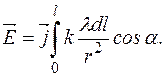
 (
( 
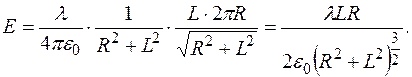



 отримаємо
отримаємо
 (12)Знайдемо вираз для напруженості поля рівномірно зарядженого поверхневою густиною заряду
(12)Знайдемо вираз для напруженості поля рівномірно зарядженого поверхневою густиною заряду 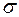 диска радіусом
диска радіусом 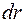 і радіусом
і радіусом  показано на мал. 7. Оскільки його товщина нескінченно мала, то на ньому розміщений нескінченно малий заряд
показано на мал. 7. Оскільки його товщина нескінченно мала, то на ньому розміщений нескінченно малий заряд 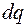 . Тому напруженість поля, яку воно створює в точці на осі кільця, згідно з результатом попередньої задачі, є
. Тому напруженість поля, яку воно створює в точці на осі кільця, згідно з результатом попередньої задачі, є
 підставлено радіус
підставлено радіус 
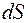 – площа виділеного нескінченно малого кільця. Очевидно, що
– площа виділеного нескінченно малого кільця. Очевидно, що  тому маємо
тому маємо



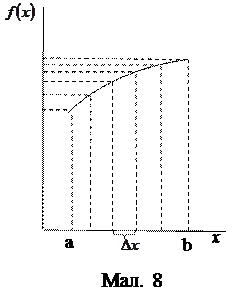 Нам слід обчислити середнє значення функції на проміжку [a, b]. Очевидно, що наближено це можна зробити, розділивши цей проміжок на п проміжків шириною
Нам слід обчислити середнє значення функції на проміжку [a, b]. Очевидно, що наближено це можна зробити, розділивши цей проміжок на п проміжків шириною  (мал. 8). Тоді
(мал. 8). Тоді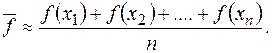


 (при цьому
(при цьому  ) сума переходить в інтеграл і дістаємо точну формулу
) сума переходить в інтеграл і дістаємо точну формулу

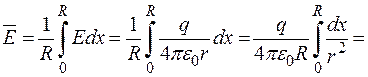


 ).
). )
)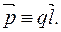
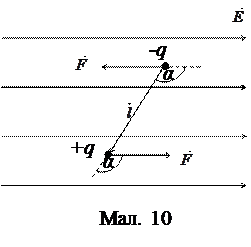 (14) Установимо, який стан займе вільний диполь, який потрапив в однорідне електричне поле.
(14) Установимо, який стан займе вільний диполь, який потрапив в однорідне електричне поле.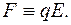 Напрями цих сил протилежні. Оскільки диполь жорсткий, то ці сили спричиняють виникнення моменту пари сил:
Напрями цих сил протилежні. Оскільки диполь жорсткий, то ці сили спричиняють виникнення моменту пари сил:

 – кут між векторами
– кут між векторами  З мал. 10 бачимо, що диполь повертатиметься доти, доки кут
З мал. 10 бачимо, що диполь повертатиметься доти, доки кут  буде діяти сила величиною
буде діяти сила величиною  в напрямку силових ліній, а на заряд
в напрямку силових ліній, а на заряд  – така ж сила проти силових ліній, тобто поле буде намагатися розірвати диполь (тоді як рівнодійна сила на диполь загалом дорівнює нулеві, що означає, що диполь буде в стані спокою).
– така ж сила проти силових ліній, тобто поле буде намагатися розірвати диполь (тоді як рівнодійна сила на диполь загалом дорівнює нулеві, що означає, що диполь буде в стані спокою). в точці на відстані
в точці на відстані  (1)
(1) – напруженість поля в певній точці, створена зарядом
– напруженість поля в певній точці, створена зарядом 
 – напруженість поля в цій же точці створена зарядом
– напруженість поля в цій же точці створена зарядом 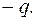

 З мал. 11 бачимо, що згідно з формулою напруженості точкового заряду
З мал. 11 бачимо, що згідно з формулою напруженості точкового заряду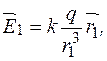
 (2)
(2) і
і  є протилежно напрямлені.
є протилежно напрямлені. і
і  і
і  .
.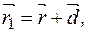
 (3)
(3)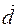 (враховуючи, що
(враховуючи, що  ):
):


 (4)
(4)

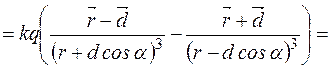

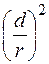 та
та  дістанемо:
дістанемо:
 , дістанемо
, дістанемо

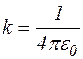
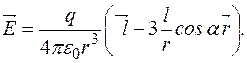 (4)
(4)

 (5)
(5) Біля заряду
Біля заряду 
 – зміна напруженості поля на відстані
– зміна напруженості поля на відстані  де
де 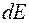 – дуже мала зміна величини вектора
– дуже мала зміна величини вектора  яка відбувається на малій відстані
яка відбувається на малій відстані  Тоді взявши до уваги, що
Тоді взявши до уваги, що  маємо
маємо
 У камері (мал. 13) створюють високий вакуум, а між зразком і стінкою камери прикладають високу напругу. Потім в камеру запускають атоми гелію чи неону. У сильному електричному полі атоми стають диполями і внаслідок неоднорідності цього поля рухаються в бік його зростання, тобто до зразка. Біля поверхні зразка поле стає настільки сильним, що воно йонізує атом, відірвавши від нього електрон. Позитивні йони гелію (чи неону) рухаються до екрана даючи на ньому зображення зразка.
У камері (мал. 13) створюють високий вакуум, а між зразком і стінкою камери прикладають високу напругу. Потім в камеру запускають атоми гелію чи неону. У сильному електричному полі атоми стають диполями і внаслідок неоднорідності цього поля рухаються в бік його зростання, тобто до зразка. Біля поверхні зразка поле стає настільки сильним, що воно йонізує атом, відірвавши від нього електрон. Позитивні йони гелію (чи неону) рухаються до екрана даючи на ньому зображення зразка.