 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Математическая модель опыта
В естественных науках познание действительности происходит с помощью анализа результатов испытаний, т.е. опыта в широком смысле. Возможный результат опыта – это событие. При изучении случайных событий, т. е. таких, которые в результате опыта могут произойти или не произойти, мы будем идеализировать реальность и пользоваться математической моделью опыта и его исходов. Например, в модельном опыте при бросании монеты может выпасть герб или цифра, тогда как в реальных условиях монета может стать на ребро (событие При построении вероятностных моделей широко используется принцип практической невозможности маловероятных событий или, что по существу то же самое, принцип практической достоверности событий, вероятность которых весьма близка к 1: если вероятность некоторого события В простейших вероятностных (статистических) моделях результаты исследований можно представить таблицей, в верхней строке которой указаны всевозможные несовместные элементарные исходы опыта, а в нижней – их вероятности (относительные частоты). Например, такая таблица, соответствующая однородной симметричной игральной кости, будет иметь вид:
где Для построения аналогичной модели появления букв русского алфавита в текстах достаточно предварительно подсчитать относительные частоты появления каждой буквы на 4 – 5 страницах литературного текста. Такой эксперимент может проделать каждый и составить соответствующую таблицу.
Сумма всех относительных частот второй строки должна быть равна 1. Небезынтересно отметить, что в литературных текстах буква «О» встречается примерно в 55 раз чаще буквы «Ф», относительная частота которой мала, но её частота повысится в математических текстах за счёт таких слов как коэффициент, функция, дифференциал и др. Указанная табличная модель имеет и практический выход: если вы посмотрите на клавиатуру компьютера или пишущей машинки с русским шрифтом, то обнаружите, что, например, клавиша с буквой «О» расположена в её центре, а с буквой «Ф» – на периферии. Клавиатура, построенная с учётом приведённой модели, создает комфорт для пользователя. В каждом языке есть своя статистическая закономерность, своя табличная модель частот, которая отражает свойства этого языка.
Поиск по сайту: |
 ). Конечно, в идеализированной модели событием
). Конечно, в идеализированной модели событием  в данном опыте весьма мала, то можно быть практически уверенным в том, что при однократном выполнении опыта событие
в данном опыте весьма мала, то можно быть практически уверенным в том, что при однократном выполнении опыта событие 
 событие – выпадение игральной кости, верхняя грань которой имеет номер
событие – выпадение игральной кости, верхняя грань которой имеет номер 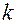 . Сумма вероятностей, находящихся во второй строке таких таблиц, равна 1.
. Сумма вероятностей, находящихся во второй строке таких таблиц, равна 1.