 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Приложения метода к решению химических задач
Сначала рассмотрим задачу из школьного учебника [35, c. 50]. Углеводород содержит в массовых долях 0,8889 или 88,89 % углерода. Его плотность по воздуху равна 1,862. Найдите молекулярную формулу этого углеводорода, напишите формулы и названия возможных его изомеров. Исключив из условия информацию о массовой доле углерода, запишем формулу углеводорода в виде
из которого видно, что Проведённые здесь вычисления могут быть автоматизированы и выполнены компьютером по соответствующей программе. Однако в результате вычислений могут быть получены и посторонние решения, а потому необходима проверка по содержанию (в нашем примере химическому) задачи. Итак, анализ, проверка результатов исполнения программы человеком или компьютером является неотъемлемой составной частью решения задачи, без которой оно не может быть признано полноценным, даже если посторонние решения и не появились! Теперь рассмотрим вариант алгоритма и программы вывода молекулярной формулы (МФ) углеводорода по массовой доле
где Поскольку в молекуле предельного углеводорода
Если при всех указанных ограничениях в результате исполнения алгоритма окажется, что существует только одна пара значений В соответствии с этим алгоритмом запишем на языке БЕЙСИК программу МФ.
10 PRINT “ВВЕДИТЕ L, A, B, E”: INPUT L, A, B, E 20 Y = 0: T = 0: K = 0 30 Y = Y + 2 40 D = L*B*Y/(A*(1- L)) 50 X = INT (D + .5) 60 IF (ABS(А*X/(A*X + B*Y) – L)> E THEN 30 70 IF Y <= 2*X+ 2 THEN T = T +1: PRINT “X = ”; X, “Y = ”; Y 80 IF T = 0 THEN PRINT “РЕШЕНИЯ НЕТ”: GOTO10 90 IF K=0 THEN K = K + 1: GOTO 30 100 IF T = 1 THEN PRINT “РЕШЕНИЕ ЕДИНСТВЕННОЕ”: GOTO10 110 PRINT “РЕШЕНИЕ НЕ ОДНОЗНАЧНОЕ”: GOTO10 120 END
Задача. Какова простейшая и молекулярная формула газообразного углеводорода, если массовая доля углерода равна 81,82 % и водорода – 18,18 %, а 10-3 м3 этого углеводорода (н.у.) имеют массу 2,6·10-3 кг? [34, с. 49]. Исключим из условия всю информацию, кроме массовой доли углерода в углеводороде, которую округлим до 0,818. Дело в том, что последняя цифра 2 массовой доли хотя и является значащей, но надёжность её точности невелика, тогда как последняя цифра числа 0,818 будет практически достоверной. Именно поэтому, исполнив программу при Дело в том, что из условия задачи лучше удалить величину 10-3м3 = 1л, как содержащую только одну значащую цифру. Самое точное данное рассматриваемой задачи 81,82 % имеет четыре значащие цифры, а потому, решая задачу, исходя только из этого значения (остальные количественные данные исключаются), компьютер выдал правильный ответ! С целью контроля проверим оба результата Последняя составляется так, что в её условие включается ответ к исходной задаче. А одно или несколько имеющих высокую точность данных исходной задачи объявляются новыми неизвестными. Если в результате решения обратной задачи новые неизвестные практически совпадут с соответствующими значениями, которые даны в условии исходной задачи, то приходим к выводу, что задача решена правильно. В условии нашей задачи самую высокую относительную точность имеет массовая доля углерода 0,8182, содержащая четыре значащие цифры. Итак, пусть Что касается второго ответа, то массовая доля углерода в углеводороде Конечно, некорректно на основании целочисленных значений относительных атомных масс записывать результат в виде, как если бы в нём содержались четыре значащие цифры. В таких случаях следует, как и выше, пользоваться табличными значениями (тогда массовая доля углерода будет 81,71 %). Значит, Итак, ответ, который выдал компьютер – правильный, так как он основан на массовой доле углерода, содержащей четыре значащие цифры! Отметим, что при округлении массовой доли углерода до значения 0,82, когда Приведём также пример, когда программа даёт ответ «РЕШЕНИЯ НЕТ». При сжигании вещества, массовая доля углерода в котором равна 60 %, образуется только оксид углерода (IV) и вода. Содержит ли это вещество кислород? Вещество, о котором идёт речь, содержит углерод, водород и возможно кислород. Допустим, что оно не содержит кислород. Тогда это – углеводород, массовая доля углерода в котором 60 %. Исполнив программу МФ при Подчеркнём, что математическая модель – это не только уравнение (14.2), но и дополнительные условия (в частности (14.3)), устанавливающие границы его применимости. Уравнение (14.2) – это только компонент математической модели. Предлагаемая программа позволяет решать также задачи для полностью замещённых галогенпроизводных углеводородов и соответствующие задачи для кремневодородов. В этих случаях величине С помощью программы МФ легко обнаруживаются лишние данные (если они имеются) в условиях соответствующих задач по химии в методических руководствах, задачниках для высших и средних учебных заведений, в пособиях для поступающих в вузы, сборниках олимпиадных задач и журнальных статьях. Эта программа может быть применена для проведения исследовательских работ на стыке таких фундаментальных дисциплин как информатика и химия. Она будет способствовать выработке навыков использования алгоритмов и ЭВМ при решении химических задач.
Поиск по сайту: |
 , тогда для определения индексов
, тогда для определения индексов 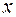 и
и 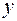 получим уравнение
получим уравнение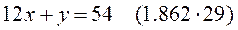 , (14.1)
, (14.1) : (1;42), (2;30), (3;18), (4;6) и
: (1;42), (2;30), (3;18), (4;6) и  – формула углеводорода (из-за несоответствия валентностей других углеводородов нет). На записи формул и названий возможных изомеров не останавливаемся: они полностью определяются найденной молекулярной формулой.
– формула углеводорода (из-за несоответствия валентностей других углеводородов нет). На записи формул и названий возможных изомеров не останавливаемся: они полностью определяются найденной молекулярной формулой.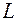 углерода в нём. Для этого запишем МФ углеводорода в виде
углерода в нём. Для этого запишем МФ углеводорода в виде  или
или , (14.2)
, (14.2) и
и  относительные атомные массы соответственно углерода и водорода. Прежде всего, отметим, что
относительные атомные массы соответственно углерода и водорода. Прежде всего, отметим, что  и
и  – натуральные числа, причём
– натуральные числа, причём 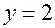 и увеличивая каждый раз его величину на 2, будем получать в соответствии с (14.2) значения
и увеличивая каждый раз его величину на 2, будем получать в соответствии с (14.2) значения 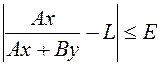 , где
, где  – граница погрешности массовой доли углерода.
– граница погрешности массовой доли углерода. с
с  , для индексов
, для индексов  любого углеводорода справедливо неравенство
любого углеводорода справедливо неравенство . (14.3)
. (14.3) = 0,001, (модуль погрешности
= 0,001, (модуль погрешности 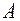 = 12,01,
= 12,01,  , получим однозначный результат:
, получим однозначный результат:  – молекулярная формула углеводорода. Ответ авторов книги:
– молекулярная формула углеводорода. Ответ авторов книги: 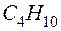 , однако он неверный.
, однако он неверный.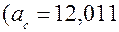 ,
,  0,8266. Оба эти числа довольно сильно отличаются от массовой доли 0,8182, содержащейся в условии исходной задачи. Значит, первый ответ (совпадающий с ответом из книги [34]) должен быть отвергнут. Уже отсюда следует, что проверка ответа – это необходимая составная часть решения задачи.
0,8266. Оба эти числа довольно сильно отличаются от массовой доли 0,8182, содержащейся в условии исходной задачи. Значит, первый ответ (совпадающий с ответом из книги [34]) должен быть отвергнут. Уже отсюда следует, что проверка ответа – это необходимая составная часть решения задачи. .
. , когда молекулярная формула может быть любой кратности
, когда молекулярная формула может быть любой кратности  , где
, где  >1 – натуральное число.
>1 – натуральное число. получим ответ «РЕШЕНИЯ НЕТ». Значит, вещество содержит кислород.
получим ответ «РЕШЕНИЯ НЕТ». Значит, вещество содержит кислород. должны быть присвоены значения относительных атомных масс соответствующих элементов.
должны быть присвоены значения относительных атомных масс соответствующих элементов.