 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
О математических моделях Земли
При построении математических моделей используют не материальные предметы, такие как дерево, пластмасса и т. п., а идеализированные, математические объекты: фигуры, параметры, произведение, равно, формула и т.п. Вообще часть плоскости может быть математической моделью многих реальных объектов. Так, древние евреи представляли Землю в виде равнины, поскольку жили в такой местности. И это представление правильно отражало действительность, конечно, приближённо и на малых площадях. Естественно, что в глубокой древности не могло быть достаточно правильных представлений о форме всей земной поверхности. География многим обязана древним грекам – эллинам. Их представления о форме Земли описаны в поэмах Гомера «Одиссее» и «Илиаде», из которых следует, что они считали Землю слегка выпуклой поверхностью, т.е. говоря современным научным языком, моделировали её шаровым или сферическим сегментом большого радиуса, когда ещё и не имели правильных представлений о форме земли в целом. Однако уже последователи знаменитого греческого учёного Пифагора – математика и философа – пошли дальше: они считали, что Земля имеет форму шара и, пытались, конечно, приближённо, определить его диаметр. Первое измерение диаметра земного шара, послужившее основанием математической географии, произвёл Эратосфен – древнегреческий математик и астроном [2, с.25 - 27], [1, с.27 - 29 ]. Знания о форме Земли и её размерах уточнялись, особенно после того, когда в 17 веке был найден метод надёжного измерения больших расстояний на ней, получивший название «триангуляция» (от латинского слова «триангулюм» - треугольник). Этот способ характерен тем, что встречающиеся на пути препятствия- холмы, леса, болота и т. п., не мешают довольно точному измерению расстояний [1, с.29 – 31 ]. Конечно, Земля не может иметь форму шара, хотя бы потому, что она вращается вокруг своей оси. На это указывал ещё великий Ньютон: в результате вращения земной шар оказался раздутым у экватора, а у полюсов сплющенным и таким образом приобрёл форму мандарина. Однако у сторонников Ньютона были и оппоненты, которые утверждали, что Земля не сплюснута, как мандарин, а наоборот вытянута подобно лимону. Научный спор между сторонниками двух противоположных утверждений длился около 50 лет. С помощью достаточно точных измерений, основанных на методе триангуляции, было установлено, что Земля имеет форму мандарина, точнее является сфероидом. Размеры земного шара, полученные таким способом, следующие: длина экваториального диаметра составляет Таким образом, форма Земли очень мало отличается от шара! Однако можно подумать, что горные вершины должны сильно искажать форму Земли. Но и это не так. Даже высочайшая гора Земного шара – Эверест (Джомолунгма), высотой почти Конечно, на отдельных участках поверхности земли, моделируемых частями плоскости, с успехом могут применяться и законы обычной (плоской) тригонометрии. В этой связи рассмотрим задачу о движении малого диаметра ядра, начальная скорость которого 1) на интересующем нас участке поверхность Земли заменяется горизонтальной плоскостью; 2) ускорение свободного падения постоянно; 3) сопротивлением воздуха при движении ядра пренебрегаем; 4) ядро считаем материальной точкой. Теперь введём систему координат. Её начало совместим с центром покоящегося ядра, ось
представляющей математическую модель рассматриваемой задачи. Исходя из этой модели, легко получить ответы на поставленные вопросы. Заметим, что при
приходим к модели, рассмотренной в §3. Задача. Какой поперечник должен иметь глобус, чтобы на нём мог быть изображён Эверест высотой около 1 мм в масштабе глобуса? [16, с.13]. Обозначим диаметр глобуса через у м, тогда, для определения неизвестного получим уравнение: (Заметим, что ответ: «Примерно 4,5 м», приведённый на с. 93 указанной книги, неверный). Итак, даже самая высокая гора Земли – Эверест (Джомолунгма), достигающая
Поиск по сайту: |

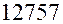 км, а длина полярного диаметра –
км, а длина полярного диаметра – 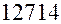 км. Эти величины показывают, что экваториальный диаметр примерно на 43 км длиннее полярного. Если изобразить отклонение формы Земли от шара на глобусе с экваториальным диаметром точно 1 м, то его полярная ось должна быть короче всего на 3,4 мм! Действительно, если
км. Эти величины показывают, что экваториальный диаметр примерно на 43 км длиннее полярного. Если изобразить отклонение формы Земли от шара на глобусе с экваториальным диаметром точно 1 м, то его полярная ось должна быть короче всего на 3,4 мм! Действительно, если 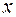 м – полярная ось глобуса, то
м – полярная ось глобуса, то 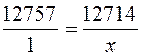 , откуда
, откуда  и
и  (м), т.е. на глобусе экваториальный диаметр отличается от полярной оси всего на 3,4 мм. Это настолько малая величина, что на глаз её невозможно обнаружить.
(м), т.е. на глобусе экваториальный диаметр отличается от полярной оси всего на 3,4 мм. Это настолько малая величина, что на глаз её невозможно обнаружить.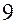 км, в масштабах указанного выше глобуса изобразится в виде прилипшей к нему песчинки диаметром около
км, в масштабах указанного выше глобуса изобразится в виде прилипшей к нему песчинки диаметром около 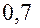 мм. Действительно, если обозначить через у м высоту изображения Эвереста на указанном глобусе, то
мм. Действительно, если обозначить через у м высоту изображения Эвереста на указанном глобусе, то  , т.е.
, т.е.  (м) или 0,7 мм. Итак, шар является математической моделью Земли, с хорошим приближением, отражающим её форму. Это обстоятельство даёт возможность использовать для различных расчетов закономерности сферической тригонометрии – математической дисциплины, изучающей зависимости между сторонами и углами сферических треугольников, образующихся при пересечении трех больших кругов сферы.
(м) или 0,7 мм. Итак, шар является математической моделью Земли, с хорошим приближением, отражающим её форму. Это обстоятельство даёт возможность использовать для различных расчетов закономерности сферической тригонометрии – математической дисциплины, изучающей зависимости между сторонами и углами сферических треугольников, образующихся при пересечении трех больших кругов сферы.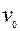 направлена под углом
направлена под углом  к поверхности Земли. Требуется установить траекторию движения центра ядра и определить расстояние на поверхности Земли от точки вылета до точки падения. Для решения этой задачи построим математическую модель, основанную на следующих допущениях (аксиомах):
к поверхности Земли. Требуется установить траекторию движения центра ядра и определить расстояние на поверхности Земли от точки вылета до точки падения. Для решения этой задачи построим математическую модель, основанную на следующих допущениях (аксиомах):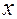 направим горизонтально в сторону движения центра ядра, ось
направим горизонтально в сторону движения центра ядра, ось 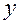 – вертикально вверх. Тогда, как известно из физики, характер движения ядра описывается системой уравнений
– вертикально вверх. Тогда, как известно из физики, характер движения ядра описывается системой уравнений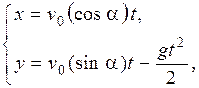
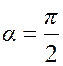
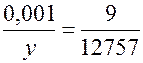 , т.е
, т.е 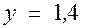 (м).
(м).