 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Случайная величина (СВ) как математическая модель
Уже в модели, связанной с бросанием игральной кости, исход опыта выражался числом выпавших очков. Существует много таких задач, в которых случайный исход опыта выражается числом, являющимся значением случайной величины. Так называют величину, которая в результате опыта может принять то или иное значение, заранее неизвестно, какое именно. Рассмотрим СВ «Размер обуви». Для продавца эта величина является случайной, поскольку ему заранее неизвестно, какой размер будет востребован покупателем. Эта СВ как и любая другая дискретная величина может быть представлена в виде табличной модели случайного опыта, в верхней строке которой будут записаны числа, соответствующие исходам опыта. Рассмотрим эксперимент по продаже обуви, проводимый в течение недели в стране, в результате которого будут подсчитаны количества пар обуви каждого размера из проданных за указанное время
Здесь Такая табличная модель случайной величины «Размер обуви» имеет большое практическое значение, так как она указывает, в каких пропорциях или процентных отношениях следует наладить производство обуви необходимых размеров, чтобы были удовлетворены потребности населения. Теперь отвлечёмся от конкретных примеров и зададим дискретную СВ
где,
Когда указанная таблица, в которой вероятности
т.е. Сумма всех значений величины
значит среднее значение Итак,
Однако при решении многих задач недостаточно знать только математическое ожидание (МО) СВ
где
Поиск по сайту: |
 пар.
пар.

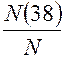

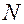 – общее число пар проданной обуви,
– общее число пар проданной обуви,  – число пар проданной обуви
– число пар проданной обуви  – го размера,
– го размера,  – относительная частота, которая в пределе при
– относительная частота, которая в пределе при  таблицей
таблицей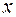
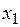


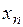

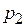
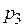
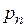
 – значение
– значение  – вероятность этого значения и
– вероятность этого значения и .
.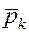 , моделирует массовые или многократно повторяемые опыты, естественно поставить вопрос о среднем значении СВ
, моделирует массовые или многократно повторяемые опыты, естественно поставить вопрос о среднем значении СВ  равна
равна  , то в серии из
, то в серии из  опытов
опытов  раз будет появляться
раз будет появляться 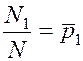 ,
, , аналогично
, аналогично 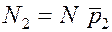 и т.д.
и т.д.  .
.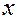 , наблюдаемых в
, наблюдаемых в  ,
,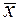 равно найденной сумме, делённой на
равно найденной сумме, делённой на  , которое в пределе при
, которое в пределе при  , совпадёт с теоретическим (идеализированным) средним значением, называемым математическим ожиданием СВ
, совпадёт с теоретическим (идеализированным) средним значением, называемым математическим ожиданием СВ 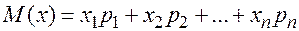 - математическое ожидание СВ
- математическое ожидание СВ  и среднее квадратическое отклонение
и среднее квадратическое отклонение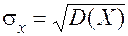 ,
, ,
,  .
.