 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Определение скорости свободного падения тела
Рассмотрим свободное падение материальной точки при отсутствии сопротивления. Начало координат совместим с начальным положением точки. При сделанных предположениях движение точки вдоль оси
Найдём среднюю скорость за малый промежуток времени от
Отсюда 6. Определение суммы ряда Для этого рассмотрим полоску бумаги А С1 С2 С3 В
Е1 Е2 Е3 Рисунок 11.1 – Модель полоски бумаги
Мысленно разрежем (или сложим) её пополам по отрезку Теперь очевидно, что
и левая часть равенства (11.2), представляющая сумму бесконечного числа слагаемых, не только имеет смысл, но и равна 1, т.е. длине всей полоски. Но как найти сумму, находящуюся в левой части равенства (11.2) , не зная заранее, что она равна 1. Для этого сначала рассмотрим сумму первых n слагаемых
представляющую для геометрической прогрессии сумму n её первых членов, которая в общем случае равна
где Теперь определим бесконечную сумму, состоящую из членов геометрической прогрессии при
Так как в случае полоски длины 1, Теперь приведём другую интерпретацию бесконечного деления отрезка (полоски), известную как апория Зенона Элейского «Дихотомия». Допуская на основе мысленного эксперимента бесконечную делимость отрезка Отметим, что великий русский писатель Л. Н. Толстой на первой странице третьей части третьего тома романа «Война и мир» приводит описание другой апории Зенона «Ахиллес и черепаха»: «Для человеческого ума непонятна абсолютная непрерывность движения. Человеку становятся понятны законы какого бы то ни было движения только тогда, когда он рассматривает произвольно взятые единицы этого движения. Но вместе с тем из этого - то произвольного деления непрерывного движения на прерывные единицы проистекает большая часть человеческих заблуждений. Известен так называемый софизм древних, состоящий в том, что Ахиллес никогда не догонит впереди идущую черепаху, несмотря на то, что Ахиллес идёт в десять раз скорее черепахи: как только Ахиллес пройдёт пространство, отделяющее его от черепахи, черепаха пройдёт впереди его одну десятую этого пространства; Ахиллес пройдёт эту десятую, черепаха пройдёт одну сотую и т. д. до бесконечности. Задача эта представлялась древним неразрешимой. Бессмысленность решения (что Ахиллес никогда не догонит черепаху) вытекала из того только, что произвольно были допущены прерывные единицы движения, тогда как движения и Ахиллеса и черепахи совершались непрерывно. Принимая всё более и более мелкие единицы движения, мы только приближаемся к решению вопроса, но никогда не достигаем его. Только допустив бесконечно – малую величину и восходящую от неё прогрессию до одной десятой и взяв сумму этой геометрической прогрессии, мы достигаем решения вопроса». Таким образом, и эта апория разрешается математически существованием суммы бесконечной прогрессии при Обратим внимание на важную роль понятия предела в науке. Она заключается в том, что только на основе предела можно давать полное определение многих встречающихся в науке величин, а затем и вычислять их значения. Так, в первом примере мы пользуемся таким определением длины окружности: длиной окружности называется предел, к которому стремится периметр вписанного в неё правильного многоугольника в процессе неограниченного увеличения числа его сторон. Существенно, что такое определение позволяет эффективно вычислять длину окружности с помощью суммы прямолинейных отрезков. Эта математическая модель длины окружности адекватна реальной ситуации. Так, если с помощью гибкой нерастяжимой нити непосредственно измерять длину окружности, ограничивающую круговой диск, то длина такой нити в виде прямолинейного отрезка в пределах точности будет совпадать с вычисленной по измеренному диаметру диска. История развития математики и её приложений показала, что важнейшим типом переменных величин, к которым удаётся свести изучение многих других, являются бесконечно малые величины, т.е. такие, которые в рассматриваемом процессе безгранично приближаются к нулю, имеют своим пределом ноль. Роль таких величин настолько велика, что всё учение об изменении величин часто и до сих пор называют «анализом бесконечно малых». Но такое определение бесконечно малой величины при практическом использовании приводит к принципиальному затруднению: ни одна реальная величина не может безгранично приближаться к нулю. Например, невозможно взять массу воды, меньше массы её молекулы, а такая масса не является бесконечно малой, только одна постоянная величина – число 0 является бесконечно малой величиной Словосочетание «бесконечно малая» по определению характеризует не размер величины, а её безграничное приближение к нулю. «Таким образом, указанное определение бесконечно малой можно применять лишь к математической моделиреального процесса, в которой действительная картина изменена так, чтобы сделать это применение возможным: мы рассматриваем маятник, который может затухать бесконечно долго, материальные тела «сплошного» (немолекулярного) строения и т. п. Эта совершенно необходимая замена реального процесса на его математическую модель должна проводиться так, чтобы изучаемые стороны процесса не потерпели бы существенного искажения. Но модель есть лишь модель, и забвение этого может привести к принципиальным ошибкам, например, к попыткам навязать без должного обоснования все свойства моделей реальной действительности. Есть и другой способ истолкования возможности практического применения бесконечно малых, и мы этим способом также будем пользоваться. Именно, практическая бесконечностьразличается от математической бесконечности. Так, «практическая» («физическая») бесконечно малая величина – это переменная или даже постоянная величина, достаточно малая по сравнению с участвующими «конечными» величинами (настолько малая, чтобы можно было без существенной ошибки применять по отношению к ней свойства «математических» бесконечно малых). В то же время эта величина не должна быть настолько малой, чтобы пришлось учитывать микроэффекты там, где это неуместно, или чтобы отрываться от реально возможных ее значений. Например, при изучении деформации упругого тела практически бесконечно малыми размерами следует считать размеры, достаточно малые по сравнению с размерами тела, но в то же время достаточно большие по сравнению с молекулярными размерами и т. п.» [30, c. 94 - 95]. В этой связи отметим, что в прикладных задачах под точкой понимают тело, размерами и формой которого можно в условиях этих задач пренебречь. Одно и то же реальное тело, в зависимости от постановки задачи, может рассматриваться как точка или как тело конечных размеров. В разных условиях точкой может считаться частица вещества, космический корабль, Земля и даже небесное тело.
Поиск по сайту: |
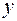 будет определяться постоянным ускорением свободного падения
будет определяться постоянным ускорением свободного падения 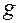 м/с2 и начальной скоростью
м/с2 и начальной скоростью 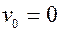 . В этих условиях, если время
. В этих условиях, если время 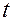 c отсчитывать от начала падения, то, как известно из курса физики, зависящая от времени координата
c отсчитывать от начала падения, то, как известно из курса физики, зависящая от времени координата 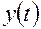 м, будет равна
м, будет равна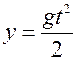 . (11.1)
. (11.1) , тогда на основании (11.1) получим
, тогда на основании (11.1) получим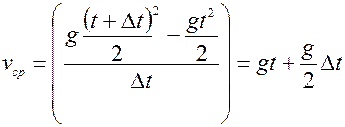 .
.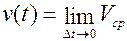 , т.е. скорость в момент времени
, т.е. скорость в момент времени 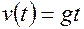 .
.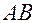 длиной 1 (дм) и шириной 1 (см) (рисунок 11.1)
длиной 1 (дм) и шириной 1 (см) (рисунок 11.1)
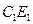 , затем разрежем (или сложим) правую часть
, затем разрежем (или сложим) правую часть 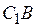 пополам по отрезку
пополам по отрезку 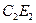 и т.д. до бесконечности. Тогда
и т.д. до бесконечности. Тогда 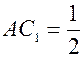 ;
; 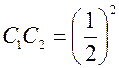 ;
; 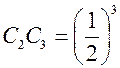 ; …
; … 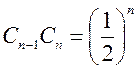 .
.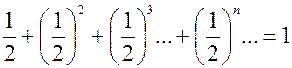 , (11.2)
, (11.2)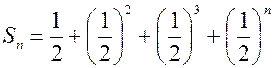 ,
,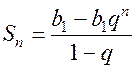 , (11.3)
, (11.3)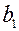 – первый член геометрической прогрессии, знаменатель которой
– первый член геометрической прогрессии, знаменатель которой 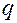 ≠ 1.
≠ 1. . Из (11.3) следует, что
. Из (11.3) следует, что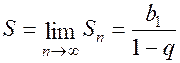 . (11.4)
. (11.4)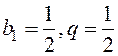 , то на основании (11.4)
, то на основании (11.4) 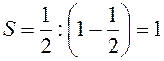 , что совпадает с (11.2). Итак, сумма членов бесконечной геометрической прогрессии при
, что совпадает с (11.2). Итак, сумма членов бесконечной геометрической прогрессии при 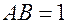 , Зенон пытался доказать, что движущееся тело (лучше точка) никогда не достигнет конца отрезка, так как для этого оно должно сначала пройти половину пути, затем ещё четверть, потом одну восьмую его часть и так до бесконечности. А поскольку бесконечное не может быть исчерпано конечным числом шагов, то движущаяся точка никогда не достигнет конца отрезка. Однако, как показано выше, бесконечная сумма, стоящая в левой части равенства (11.2), равна 1. Именно поэтому указанное противоречие математически разрешается равенством (11.2) или формулой (11.4).
, Зенон пытался доказать, что движущееся тело (лучше точка) никогда не достигнет конца отрезка, так как для этого оно должно сначала пройти половину пути, затем ещё четверть, потом одну восьмую его часть и так до бесконечности. А поскольку бесконечное не может быть исчерпано конечным числом шагов, то движущаяся точка никогда не достигнет конца отрезка. Однако, как показано выше, бесконечная сумма, стоящая в левой части равенства (11.2), равна 1. Именно поэтому указанное противоречие математически разрешается равенством (11.2) или формулой (11.4). (в общем случае при
(в общем случае при