 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Вероятностные модели конкретных задач
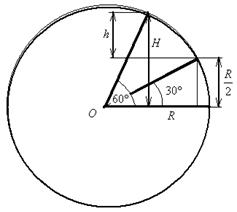
Задача 1. Спутник Земли движется по орбите, которая заключена между 60° северной широты и 60° южной широты. Определить вероятность того, что спутник упадёт на поверхность Земли выше 30° северной широты. При решении будем исходить из того, что математической моделью Земли является шар, радиус которого обозначим через
. Рисунок 16.1– Модель сечения Земли меридианной плоскостью
Для инженера вероятность, пусть и грубо, – это относительная частота, процент, с которым появляется то или иное событие в соответствующем эксперименте. Рассмотрим решение вероятностной задачи методом статистического моделирования, а затем такой подход используем и для вывода формул. Задача 2. Один стрелок даёт 80 % попаданий в мишень, другой (при тех же условиях стрельбы) – 70 % . Найти вероятность (процент) попадания в мишень обоими стрелками, если они стреляют внеё одновременно (залпом). Допустим, что произведено С аналогичными моделями встречаются учащиеся средней школы при решении задач на движение, в котором, например, скорость 20 км/час принимается (по умолчанию) точно равной этому значению в любые промежутки и даже моменты времени, тогда как в реальном процессе движения мы не можем её определить абсолютно точно! Итак, в нашей модели первый стрелок попадёт в мишень 0,80 В нашей модели также предполагается, что оба стрелка стреляют независимо друг от друга: попадание или промах одним стрелком не зависит от того, попал или промахнулся другой. Подчеркнём, что в предложенной модели использовались дедуктивные рассуждения (т.е. рассуждения без обращения к натурным испытаниям, однако при этом допустимы мысленные эксперименты). Теперь установим методом статистического моделирования теорему умножения: Если события В На основе статистического определения вероятности события могут быть получены и другие формулы. Задача 3. (Детская энциклопедия, Т. 2, просвещение, 1965 – С. 461). Рыбоводу понадобилось определить, сколько в озере рыб, годных для улова. Следуя рекомендациям теории вероятностей, рыбовод забросил сеть с заранее выбранным размером ячеек и, вытащив ее, пересчитал добычу. Рыб оказалось 38. Сделав пометку на каждой рыбке, рыбовод всех их выпустил в озеро. На другой день он забросил ту же самую сеть и теперь выловил уже 53 рыбки, две из которых оказались меченными. По этим данным рыбовод и вычислил приблизительно количество рыб в озере, годных для улова данной сетью. К какому результату пришел рыбовод? Решение. Пусть число рыб в озере, годных для улова данной сетью, равно Задача 4. Завод выпускает массовую продукцию. Если изделие, выпущенное заводом и поступившее в продажу, выходит из строя в течение года, то требуется заменить его запасным. Сколько необходимо запасных изделий, если в течение года продаётся Если обозначить через
Отметим, что по такой схеме (модели) приближённо определяют урожай на плантации по урожаю на некотором числе небольших участков, а также многие другие величины. В этом контексте вспомним о работе отечественных математиков в годы Великой Отечественной войны в помощь фронту по организации производственных процессов, направленных на повышение производительности труда и на улучшение качества военной продукции. Здесь было много проблем. Одна из них – это контроль качества продукции. Например, изготовленные снаряды должны обладать определенной кучностью при стрельбе, но для проверки такого свойства необходимо проводить опытные стрельбы. А если так испытывать все снаряды, то, что же останется? Так возникла задача: по испытаниям малой выборки изделий судить о качестве всей партии. Во время войны решением таких задач для нужд фронта занимались главным образом А.Н. Колмогоров и Б.В. Гнеденко. Они предложили использовать статистические методы текущего контроля, т.е. такую организацию производственного процесса, в которой уже при изготовлении был поставлен заслон выпуску некачественной продукции. Как отмечает Б.В. Гнеденко: «После окончания войны выяснилось, что аналогичные исследования проводили математики США. Они подсчитали, что результаты их работы принесли за годы войны стране миллиардную экономию. То же самое можно сказать и о работе советских математиков и инженеров». В этой связи укажем, что в США в годы второй мировой войны некоторые статистические методы были засекречены, а такой важный способ интенсификации производства стали, как использование кислорода, засекречен не был. Это говорит о том, какое большое значение придавалось прикладным математическим методам во время войны.
Поиск по сайту: |
 и падение спутника равновозможно в любом «месте» шарового пояса между 60° северной широты и 60° южной широты. Так как площадь
и падение спутника равновозможно в любом «месте» шарового пояса между 60° северной широты и 60° южной широты. Так как площадь 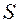 шарового пояса между указанными широтами равна
шарового пояса между указанными широтами равна 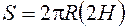 , где (рисунок 16.1)
, где (рисунок 16.1) 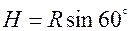 - половина высоты шарового слоя, а площадь
- половина высоты шарового слоя, а площадь  шарового пояса выше 30° северной широты и ниже 60° северной широты будет
шарового пояса выше 30° северной широты и ниже 60° северной широты будет 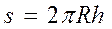 , где
, где  , то искомая вероятность
, то искомая вероятность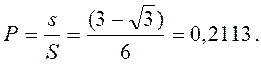
 двойных выстрелов (залпов). В нашей идеализированной расчётной схеме (модели) предполагается, что при всех сериях залпов соответствующий стрелок даёт точно 80 % и 70 % попаданий в мишень. В действительности эти величины являются средними статистическими.
двойных выстрелов (залпов). В нашей идеализированной расчётной схеме (модели) предполагается, что при всех сериях залпов соответствующий стрелок даёт точно 80 % и 70 % попаданий в мишень. В действительности эти величины являются средними статистическими.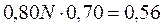
 таких, в которых в мишень попадёт и первый и второй стрелок, т.е. вероятность (статистическая, когда
таких, в которых в мишень попадёт и первый и второй стрелок, т.е. вероятность (статистическая, когда 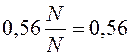 или 56 %.
или 56 %. и
и  независимы в данном опыте, то вероятность их произведения (совместного наступления) равна произведению вероятностей этих событий.
независимы в данном опыте, то вероятность их произведения (совместного наступления) равна произведению вероятностей этих событий. опытах, в которых
опытах, в которых 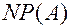 раз наступит событие
раз наступит событие  появится и событие
появится и событие 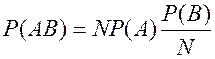 при
при 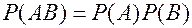 .
.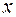 . Тогда отношение числа меченых рыб к числу всех рыб, опять - таки годных для улова данной сетью, равно
. Тогда отношение числа меченых рыб к числу всех рыб, опять - таки годных для улова данной сетью, равно  . Во второй раз рыбовод выловил 53 рыбы, из них две меченые. Следовательно, отношение числа меченых рыб к числу выловленных равно
. Во второй раз рыбовод выловил 53 рыбы, из них две меченые. Следовательно, отношение числа меченых рыб к числу выловленных равно 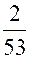 . Будем предполагать, что меченые рыбы равномерно распределились среди всех рыб в водоеме, тогда оба отношения примерно одинаковы:
. Будем предполагать, что меченые рыбы равномерно распределились среди всех рыб в водоеме, тогда оба отношения примерно одинаковы: 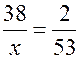 , откуда
, откуда 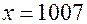 . Значит, в озере имеется примерно тысяча рыб, годных для улова данной сетью.
. Значит, в озере имеется примерно тысяча рыб, годных для улова данной сетью. – число вышедших из строя в течение года изделий, то их относительная частота будет
– число вышедших из строя в течение года изделий, то их относительная частота будет  . Если в течение года испытать выборку малого объёма n, в которой
. Если в течение года испытать выборку малого объёма n, в которой 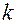 изделий вышло из строя, то их относительная частота будет
изделий вышло из строя, то их относительная частота будет 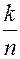 . Поэтому
. Поэтому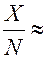
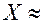
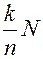 .
.