 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Взаимно простые числа в химии
В литературе по химии можно встретить такую формулировку закона Гей-Люссака: “Объёмы вступающих в реакцию газов при одинаковых условиях относятся друг к другу и к объёмам образующихся газообразных соединений как простые целые числа”. Однако, например, при сгорании одного объёма бутана В различных химических изданиях закон кратных отношений формулируется в виде: “Если два элемента образуют между собой несколько соединений, то весовые количества одного элемента, соединяющиеся с одним и тем же весовым количеством другого, относятся между собой как небольшие целые числа”. Но рассмотрим два углеводорода
будут большими. По этой причине и в формулировке закона кратных отношений слова “небольшие целые” лучше заменить на “взаимно простые” [42, с. 78]. Отметим также, что простейшую формулу химического соединения можно определить как такую, индексы при элементах которой являются взаимно простыми числами. Многие закономерности химии могут быть четко сформулированы в виде теорем.
Критерии алканов Теорема 1 (Критерий 1). Углеводород с простейшей формулой
Действительно, если выполнены условия теоремы, то простейшая формула углеводорода должна совпадать с простейшей формулой алкана и поэтому имеет место уравнение (18.1), корнем которого будет натуральное число Например, если простейшая формула углеводорода Если простейшая формула углеводорода – Теорема 2. Если углеводород – алкан, то массовая доля углерода в нем меньше массовой доли углерода в этилене. Действительно, записав формулу алкана в виде
где левая часть неравенства равна массовой доле углерода в алкане, а правая – в этилене ( Справедлива и Теорема 3 (обратная к теореме 2).Если массовая доля углерода в углеводороде меньше массовой доли углерода (»85.7 %) в этилене, то углеводород – алкан. Действительно, записав формулу углеводорода как Теорема 4 (Критерий 2).Углеводород – алкан, тогда и только тогда, когда массовая доля углерода в углеводороде меньше массовой доли (»85,7 %) углерода в этилене. Задача 1. Какова простейшая и молекулярная формула газообразного углеводорода, если массовая доля углерода равна 81,82 % и водорода – 18,18 %, а 10-3 м3 этого углеводорода (н.у.) имеют массу 2,6·10-3 кг? [34, с. 49]. Эта задача была решена методом вычислительного эксперимента в пункте 14.2. Здесь приведём ещё решение, основанное на теореме 3. Учитывая, что массовая доля углерода в этилене составляет 85,7 % и 81,82 % < 85,7 %, на основании теоремы 4 заключаем, что углеводород, о котором идёт речь в задаче – алкан. Поэтому его формула имеет вид Теоремы гомологии Теорема 5. Если известно, какому гомологическому ряду принадлежит углеводород, то молекулярная формула такого углеводорода однозначно определяется его относительной молекулярной массой [43 с. 72]. Действительно, если выполняются условия этой теоремы, то индексы при углероде и водороде зависят только от одного неизвестного Задача 2.Выведите формулу диенового углеводорода, если при сгорании его объемом 4 л образовался оксид углерода объемом 12 л и пары воды объемом 8 л. Плотность паров по водороду 20 [15, с. 60]. В соответствии с теоремой 5 исключим из условия этой задачи всю информацию, кроме плотности диенового углеводорода по водороду. Тогда, записав общую формулу такого углеводорода как Теорема 6.Если известно, какому гомологическому ряду принадлежит углеводород, за исключением ряда Дело в том, что все углеводороды ряда Руководствуясь теоремой 6, используем из условия задачи 2 информацию, определяющую простейшую формулу диенового углеводорода: 8 л об объеме паров воды и 12 л об объеме оксида углерода, пусть даже неизвестно какого. Запишем его формулу как из которого найдём, что Теорема 7. Если указано, какому гомологическому ряду принадлежит углеводород и известен индекс при Действительно, если выполняются условия этой теоремы, то индексы при углероде и водороде зависят только от одного параметра В соответствии с этой теоремой исключим из условия задачи 2 информацию о плотности углеводорода и объеме оксида углерода (тем более, что в условии не указано, о каком оксиде идет речь). Тогда, записав общую формулу диенового углеводорода как
на основании следствия из закона Авогадро имеем
(предполагается, что объемы измерены при одинаковых условиях), откуда находим индекс при Теперьиспользуем из условия задачи 2 данное 4 л, а также информацию об объеме оксида углерода, пусть даже неизвестно какого. Запишем его формулу как
Задача 3. Этиленовые углеводороды широко используются в промышленности для синтеза полимеров. Этиленовый углеводород объемом Сначала исключим из условия этой задачи данное « Запишем формулу этиленового углеводорода в виде
( Теперьисключим из условия всю информацию кроме той, что этиленовый углеводород объемом
и обозначив через
( Приведем ещё решение, при котором исключим из условия информацию «объемом 120 мл, взятым в избытке». Тогда, учитывая, что при пропускании смеси газов через раствор щелочи остаток составил 30 мл и углеводород был взят в объеме 30 мл, то в избытке он не мог оказаться. Следовательно, в избытке был кислород. Так как объем образовавшегося в результате реакции оксида углерода (IV) составил 90 – 30 = 60 (мл), то, записав формулу этиленового углеводорода в виде Рассмотрим также решение, при котором удалим из условия слова “взятым в избытке” и “объем их составил 90 мл”. Тогда, как и выше, заключаем, что в избытке был кислород, в 120 мл которого полностью сгорает 30 мл этиленового углеводорода и вновь приходим к выводу, что И, наконец, приведем решение, при котором исключимлишнюю неколичественную информацию, переформулировав задачу:Смешали углеводород объемом 30 мл с кислородом объемом 120 мл и подожгли. После окончания реакции и приведения смеси газов к первоначальным условиям (вода конденсируется) объем их составил 90 мл, а после её пропускания через раствор щелочи объем уменьшился до 30 мл. Назовите углеводород, о котором идет речь. Учитывая, что при пропускании смеси газов через раствор щелочи остаток составил 30 мл и углеводород был взят в объеме 30 мл, то в избытке он не мог оказаться. Следовательно, в избытке был кислород. Значит, объем прореагировавшего кислорода равен 120 – 30 = 90 (мл), а объем образовавшегося в результате реакции углекислого газа составляет 90 –30 = 60 (мл). Теперь, обозначив формулу углеводорода как Задача 4. Два насыщенных углеводорода имеют одинаковый элементный состав: 85,614 % Поскольку два насыщенных углеводорода имеют одинаковый процентный состав элементов и разные плотности, то они не могут принадлежать к гомологическому ряду метана. Следовательно, насыщенные углеводороды, о которых идёт речь в задаче, содержат циклы, а потому их общая формула –
Поиск по сайту: |
 образуется четыре объёма оксида углерода
образуется четыре объёма оксида углерода  :
:  и
и 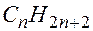 , в которых натуральное число n может быть и большим, а тогда и члены отношений
, в которых натуральное число n может быть и большим, а тогда и члены отношений
 – алкан
– алкан  в том и только в том случае, если натуральное число
в том и только в том случае, если натуральное число  есть корень уравнения
есть корень уравнения . (18.1)
. (18.1)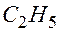 , то на основании теоремы 1, из уравнения
, то на основании теоремы 1, из уравнения  находим натуральное число
находим натуральное число  . Значит,
. Значит,  – молекулярная формула углеводорода. Если простейшая формула углеводорода –
– молекулярная формула углеводорода. Если простейшая формула углеводорода –  , то на основании той же теоремы из уравнения
, то на основании той же теоремы из уравнения  получаем ненатуральное число n = –3. Это значит, что углеводород – не алкан.
получаем ненатуральное число n = –3. Это значит, что углеводород – не алкан. , то на основании теоремы 1 из уравнения
, то на основании теоремы 1 из уравнения 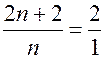 имеем 2n + 2 = 2n или 2 = 0, т.е. указанное уравнение решения не имеет. Значит и натуральное число n не является корнем этого уравнения. По той же теореме заключаем, что рассматриваемый углеводород – не алкан
имеем 2n + 2 = 2n или 2 = 0, т.е. указанное уравнение решения не имеет. Значит и натуральное число n не является корнем этого уравнения. По той же теореме заключаем, что рассматриваемый углеводород – не алкан , получим
, получим ,
, и
и  соответственно относительные атомные массы углерода и водорода).
соответственно относительные атомные массы углерода и водорода). и по условию теоремы 3 неравенство
и по условию теоремы 3 неравенство  , из которого следует:
, из которого следует:  . Но
. Но 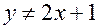 , так как число атомов водорода в молекуле любого углеводорода – четное, тогда как число
, так как число атомов водорода в молекуле любого углеводорода – четное, тогда как число  при каждом натуральном
при каждом натуральном 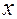 – нечетное и не может быть
– нечетное и не может быть 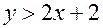 , поскольку максимальное число атомов водорода, которые могут соединиться с
, поскольку максимальное число атомов водорода, которые могут соединиться с  в предельном нециклическом углеводороде. Следовательно,
в предельном нециклическом углеводороде. Следовательно,  , и
, и  – формула алкана. Теперь обе теоремы (прямую и обратную) объединим в одну. Итак,
– формула алкана. Теперь обе теоремы (прямую и обратную) объединим в одну. Итак,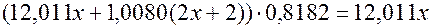 , из которого получаем
, из которого получаем  , и так как
, и так как 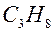 – молекулярная формула углеводорода, которая совпадает с его простейшей формулой.
– молекулярная формула углеводорода, которая совпадает с его простейшей формулой. , получим для определения неизвестного
, получим для определения неизвестного 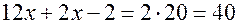 , из которого
, из которого  . Значит, формула диенового углеводорода –
. Значит, формула диенового углеводорода –  или
или 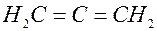 .
. , то молекулярная формула такого углеводорода однозначно определяется его простейшей формулой.
, то молекулярная формула такого углеводорода однозначно определяется его простейшей формулой.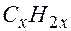 имеют одну простейшую формулу
имеют одну простейшую формулу  , и потому только по ней найти молекулярную формулу гомолога невозможно. Во всех других случаях
, и потому только по ней найти молекулярную формулу гомолога невозможно. Во всех других случаях  . Тогда, на основании общей формулы диенового углеводорода
. Тогда, на основании общей формулы диенового углеводорода  и схемы реакции
и схемы реакции  +
+  , составим уравнение
, составим уравнение 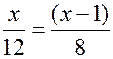 ,
,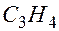 или
или  .
. его молекулярной формулы, то она определяется однозначно.
его молекулярной формулы, то она определяется однозначно.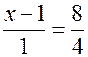
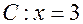 . Значит, формула диенового углеводорода запишется как
. Значит, формула диенового углеводорода запишется как  →
→  ,откуда
,откуда  , и снова
, и снова  .
. мл смешали с кислородом объемом
мл смешали с кислородом объемом  мл, взятым в избытке, и подожгли. После приведения смеси газов к первоначальным условиям (вода конденсируется) объем их составил
мл, взятым в избытке, и подожгли. После приведения смеси газов к первоначальным условиям (вода конденсируется) объем их составил  мл, а после поглощения смеси газов раствором щелочи объем газов составил
мл, а после поглощения смеси газов раствором щелочи объем газов составил  →
→ 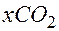 . Обозначим через
. Обозначим через  мл объем углекислого газа, образованного в результате полного сгорания
мл объем углекислого газа, образованного в результате полного сгорания  ,
, , поскольку в 90 мл входят и углекислый газ, и избыток кислорода). Значит,
, поскольку в 90 мл входят и углекислый газ, и избыток кислорода). Значит,  или
или 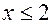 , так как
, так как  , ибо неизвестный углеводород – этиленовый. Поэтому индекс при
, ибо неизвестный углеводород – этиленовый. Поэтому индекс при 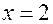 и по теореме 7 формула углеводорода примет вид
и по теореме 7 формула углеводорода примет вид  или
или  .
.
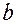 мл объем кислорода, нужного для сгорания
мл объем кислорода, нужного для сгорания 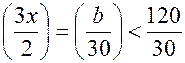
 , так как в 120 мл входит и избыток кислорода), из которого следует, что
, так как в 120 мл входит и избыток кислорода), из которого следует, что  . Но
. Но  , т.е. натуральное число
, т.е. натуральное число  , т.е.
, т.е.  –формула углеводорода.
–формула углеводорода.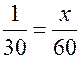 находим индекс при С:
находим индекс при С:  и записав уравнение реакции 4
и записав уравнение реакции 4 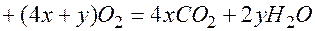 на основании следствия из закона Авогадро, получим систему:
на основании следствия из закона Авогадро, получим систему:  и
и  , из которой находим индексы при
, из которой находим индексы при  :
: 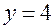 и
и  и
и  , на основании формулы
, на основании формулы  и
и  , из которых находим
, из которых находим 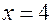 и
и  . Поэтому молекулярные формулы углеводородов будут
. Поэтому молекулярные формулы углеводородов будут  и
и  . На записях структурных формул изомеров не останавливаемся.
. На записях структурных формул изомеров не останавливаемся.