 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
И обусловленности задач
Если решение некоторой задачи сводится даже к системе линейных алгебраических уравнений, то известная теория построена в предположении, что все коэффициенты, включая и правые части, заданы точно. Такое предположение естественно для классической математики, но не всегда приемлемо в приложениях. Действительно, когда система моделирует связи между реальными величинами, то ее коэффициенты имеют конкретный смысл. Они часто получаются в результате измерений (прямых или косвенных) и поэтому известны приближенно. Но тогда приходится решать систему, в которой известные величины заданы приближенно. Не так уж редко в таких случаях малые погрешности в исходных данных вызывают достаточно большие погрешности в решениях, которые таким образом оказываются практически непригодными, неустойчивыми, а соответствующие им задачи плохо обусловленными. Конечно, при рассмотрении прикладных задач важно знать, какое решение найдено: неустойчивое или устойчивое, добротное, которое может быть использовано на практике. Ответ на этот вопрос можно получить на основе применения ЭВМ [38]. Например, решение химической задачи, взятой из журнала «Химия в школе»: «При сгорании 10,0 г смеси этанола и диэтилового эфира образовалось 12,0 г воды. Определите массы соединений в исходной смеси», сведено к системе линейных уравнений
и получен ответ: Для анализа обусловленности задачи целесообразно составить программу решения указанной системы и с помощью ЭВМ находить
Однако, изменив исходные данные 10,0 и 12,0 на 0,5 единицы последнего сохраненного разряда, воспользуемся, например, такими их значениями соответственно: 9,95 и 12,05 (остальные коэффициенты оставлены без изменения) и исполнив на ЭВМ программу, получим ответ: Теперь рассмотрим задачу, условие которой приводится в методических пособиях и задачниках по химии. Хлоропроизводное предельного углеводорода имеет относительную молекулярную массу 237. Состав этого соединения следующий: Прежде всего, исключим из условия задачи информацию о том, что относительная молекулярная масса соединения равна 237. Тогда, обозначив формулу через
где
решая которую по соответствующей программе, найдем: Далее изменим, исходные данные 0,899 и 0,101 на 0,5 единицы последнего сохраненного разряда, так, чтобы их сумма равнялась 1, т.е. здесь мы будем исследовать на устойчивость решение при условии, что сумма процентных содержаний хлора и углерода в соединении равна 100 % (так называемая условная устойчивость). Взяв вместо 0,899 значение 0,8995, мы должны вместо 0,101 взять 0,1005, тогда второе уравнение системы (23.4) не изменится, а первое примет вид:
Теперь, решая модифицированную систему (21.4) с учётом того, что неизвестные величины являются натуральными числами, вновь получим тот же самый ответ:
Ещё раз подчеркнем, что, несмотря на исключение из условий задачи относительной молекулярной массы, равной 237, задача оказалась хорошо обусловленной, а её решение – устойчивым, добротным.
Уменьшение числа аксиом является все же достижением. Г. Лейбниц УПРОЩЕНИЕ МОДЕЛЕЙ
В этом параграфе рассматриваются упрощения содержательных моделей в виде текстовых задач. При этом упрощать можно как сам текст, так и соответствующую ему математическую модель, но так, чтобы упрощения не изменяли содержание самой задачи или её математической модели, которые остаются адекватными исходным формулировкам и моделям. Таким образом, мы будем анализировать условия задач и удалять из них лишние данные, если такие имеются. Химические задачи В учебниках, справочниках, пособиях для поступающих в вузы и журнальных материалах нередко встречаются задачи на вывод формул соединений, причем в условиях оказывается лишних сведений, как количественных, так и качественных иной раз столько, что, удаляя их, задачу можно решить несколькими способами, используя при этом различные группы исходных данных. Продемонстрируем сказанное возможными вариантами рассматриваемых ниже решений. При этом для сокращения текста будем пользоваться леммой: Для индексов
Действительно, для индексов молекулярной формулы
Задача 1.Смешали газообразный углеводород объемом 40 мл с кислородом объемом 200 мл, который взят в избытке и подожгли. После приведения полученной смеси газов к первоначальным условиям (вода конденсируется) объем их составил 140 мл, из которых 80 мл поглощено щелочью при пропускании через нее газов. Установите формулу углеводорода [15, с. 38]. Решение первое.Исключим из условия информацию о том, что кислород был взят в избытке. Так как в результате реакции образовалось 80 мл
на основании следствия из закона Авогадро, получим систему
из которой находим: Решение второе. Исключим из условия данное «40 мл». Поскольку объем не прореагировавшего кислорода равен Решение третье. Исключим из условия информацию о том, что кислород был взят в избытке и данное «40 мл», т.е. решим задачу: Смешали газообразный углеводород с 200 мл кислорода и подожгли. После окончания реакции и приведения полученной смеси газов к первоначальным условиям (вода конденсируется) объем их составил 140 мл, из которых 80 мл поглощено щелочью при пропускании через неё газов. Установите формулу углеводорода. Так как в результате реакции образовалось 80 мл Задача 2.Смесь 5 мл газообразногоуглеводорода с 12 мл кислорода поместили в эвдиометр и взорвали. После приведения условий к первоначальным объем газовой смеси составил 7 мл, а после её пропускания через раствор щелочи уменьшился до 2 мл, причем оставшийся газ поддерживал горение. Определите формулу углеводорода [Н.Е. Кузьменко, В.В.Еремин, В.А. Попков. Начала химии. Современный курс для поступающих в вузы, Т.2. - М.: ЭКЗАМЕН, 2004, с. 138]. Решение первое.Исключим из условия количественное данное «12 мл» и сведение о том, что «оставшийся газ поддерживал горение». Поскольку после пропускания смеси газов через раствор щелочи объем уменьшился до 2 мл, то один из газов был взят в избытке. Предположим, что в избытке был неизвестный углеводород, формулу которого обозначим как
Тогда объем прореагировавшего углеводорода будет 5–2=3 (мл) и на основании уравнения реакции и следствия из закона Авогадро имеем пропорцию Решение второе. Удалим из условия количественное данное «5 мл» и сведение о том, что «оставшийся газ поддерживал горение». Так как после пропускания смеси газов через раствор щелочи объем уменьшился до 2 мл, то один из газов был взят в избытке. Если в избытке был углеводород
получим пропорцию
Решение третье.Исключим информацию «12 мл» и «до 2 мл». Поскольку оставшийся газ поддерживал горение, то кислород был взят в избытке. Если принять объем
Решение четвертое. Исключим из условия информацию о том, что объем газовой смеси составил 7 мл и после её пропускании через раствор щелочи уменьшился до 2 мл. Иными словами, найдем формулу углеводорода, 5 мл которого сгорают в 12 мл кислорода, взятого в избытке. Обозначим через
( или из которого Поскольку в молекуле любого углеводорода число атомов водорода четное Решение пятое.Исключим из условия слова «а после её пропускания через раствор щелочи уменьшился до 2 мл, причем оставшийся газ поддерживал горение». Поскольку объем газовой смеси (
получим систему
из первого уравнения которой имеем Значит, не существует углеводород, который может быть в избытке. Итак, в избытке был кислород и на основании уравнения реакции справедливо соотношение Задача 3.К 300 мл смеси некоторого углеводорода с аммиаком добавили избыток кислорода и подожгли. После полного сгорания газов исследуемой смеси объем вновь полученной смеси составил 1250 мл. После конденсации паров воды он сократился до 550 мл, после обработки щелочью – до 250 мл, 150 мл из которых приходилось на долю кислорода. Объемы всех газов измерены при одинаковых условиях. Установите формулу углеводорода [Химия в школе, №1, 1993, с.39]. Решение первое.Заменим первое предложение из условия этой задачи таким «К смеси некоторого углеводорода с аммиаком добавили кислород и подожгли», а остальной текст оставим без изменения. Так как после полного сгорания газов исследуемой смеси 150 мл приходилось на долю кислорода, то он был взят в избытке. Смесь, образовавшаяся после полного сгорания газов, содержит: 1250 – 550 = 700 (мл) паров 550 –250 = 300 (мл) Решение второе. Сначала переформулируем условие:К 300 мл смеси некоторого углеводорода с аммиаком добавили кислород и подожгли. После полного сгорания газов исследуемой смеси объем вновь полученной смеси составил 1250 мл. После конденсации паров воды он сократился до 550 мл, после обработки щелочью – до 250 мл, 150 мл из которых приходилось на долю некоторого газа. Объемы всех газов измерены при одинаковых условиях. Установите формулу углеводорода. В конечных продуктах содержится азот и кислород. Предположим, что 150 мл составляет азот. Тогда из неполного уравнения реакции 2 Уже отсюда следует, что Решение третье. Исключим информацию об объеме смеси, равном 300 мл и воспользуемся общим уравнением реакции горения, которое, с точки зрения системного подхода (анализа) больше соответствует реальному химическому процессу. Пусть сгорают
Как показано выше, смесь, образовавшаяся после полного сгорания газов, содержит: 700 мл паров воды, 300 мл углекислого газа, 100 мл азота и потому коэффициенты перед
а коэффициенты перед
Значит, Задача 4.При сжигании 6,45 ггазообразного галогеналкана образовалось 4,48 л углекислого газа и 2,24 л хлороводорода (н.у.); плотность неизвестного вещества при н.у. равна 2,879 г/л. Выведите молекулярную формулу вещества [25, с. 4]. Исключим из условия всю информацию, кроме той, что плотность газообразного галогеналкана при н.у. равна 2,879 г/л, да и ту округлим до трех значащих цифр: 2,88 г/л. Отсюда, с точностью до трёх значащих цифр, относительная молекулярная масса галогеналкана Задача 5. Плотность по водороду вещества, имеющего массовый состав: 54,55 % углерода, 9,09 % водорода, 36,36 % кислорода, равна 22. Оно легко восстанавливает оксид серебра, образуя кислоту. Определите молекулярную формулу этого вещества и назовите его. К какому гомологическому ряду оно относиться? [25, с.22]. Исключим из задачи количественные данные о процентах. Тогда на основании сохранённой информации приходим к выводу, что вещество – альдегид, состоящий из Задача 6.Одноосновная карбоновая кислота имеет следующий состав: углерод 40,0 %, водород 6,67 %, кислород – 53,33 % Плотность паров этой кислоты по аргону равна 1,5. Исходя из этих данных, найдите молекулярную формулу этой кислоты [25, с.22]. Сохраним информацию о том, что карбоновая кислота состоит из углерода, водорода и кислорода и плотность её паров по аргону равна 1,5. Тогда Задача 7.Определите молекулярную формулу газа, если известно, что при сжигании 2,24 л его образовалось 4,48 л углекислого газа (н.у.) и 1,8 г воды. Плотность газа по воздуху равна 0,8966 [25, с.4]. Удалим всю количественную информацию кроме плотности газа по воздуху, да и ту округлим до двух значащих цифр: 0,90. Формулу газа запишем в виде Задача 8. Какова масса серной кислоты, которую можно получить из 16 т руды, содержащей 60 % пирита Прежде чем решать эту и последующие задачи, заметим, что, если химический процесс получения какого - либо вещества состоит из нескольких стадий, а все атомы некоторого элемента в каждой стадии переходят из исходного вещества только в один конечный продукт, то нерационально пользоваться расчётами по уравнениям всех промежуточных реакций. В таких случаях целесообразно воспользоваться одной обобщённой схемой, в которой указаны только формулы одного исходного вещества и соответствующего конечного продукта. Для решения рассматриваемой задачи сначала запишем схемы протекания реакций. 1. Обжиг пирита: 2. Окисление оксида серы (IV): 3. Получение серной кислоты: Поскольку во всех превращениях цепочки
только указанные начальные и конечные продукты содержат в своём составе серу
в которой коэффициенты уравнены по атомам Так как Теперь из схемы (22.3) очевидно, что m( (отметим, что решение автора книги занимает две страницы, а ответ 15,68 т – некорректный, так как результат не может быть точнее исходных данных и должен в соответствии с правилами приближённых вычислений содержать две значащие цифры). Задача 9. Сколько тонн 98 % раствора серной кислоты можно получить из 2,4 т пирита? (там же, c. 152 – 153). Сначала найдём количество вещества пирита Теперь из той же схемы (22.3) следует: n Значит, Следовательно, Задача 10. Какой объем аммиака (н. у.) потребуется для получения 50 т раствора, содержащего 0,5 массовых долей азотной кислоты? [там же, c. 168 – 169]. Сначала запишем схемы протекания реакций, которые используются для получения азотной кислоты 1. Окисление аммиака кислородом:
2. Окисление оксида азота (II) до оксида азота (IV):
3. Поглощение оксида азота (IV) водой:
Отсюда следует, что для получения азотной кислоты используется цепочка превращений Теперь найдём количество вещества азотной кислоты
а затем на основании расчётной схемы приходим к выводу, что
(ответ автора 8889 м3 некорректный, так как результат должен содержать одну значащую цифру, как и массовая доля 0,5. В этой связи ещё раз подчеркнём, что нули, входящие в приближенные числа, записанные прописью тыс., млн. и т.п. – значащими не являются). Математические задачи Задача 1.Найти вероятность На основании равенств
Р(А+В) = Р(А) + Р(В) – Р(АВ) имеем:
т.е. результат не зависит от Задача 2.Найти вероятность Из равенства Задача 3.Разыграть пять пар возможных значений случайной величины (
У к а з а н и е. Для определённости принять при разыгрывании Найдем закон распределения составляющей р1 = Р(Х = х1) = 0,20 +0,30 = 0,50; р2 = Р(Х = х2) = 0,08+0,12 = 0,20; р3 = Р(Х = х3) = 0,12+0,18 = 0,30. Проверка: 0,50 +0,20 + 0,30 = 1. Итак, закон распределения СВ Х х1 х2 х3 р 0,50 0,20 0,30 Аналогично находим закон распределения Y y1 у2 р 0,40 0,60 Поскольку Р((Х = хi) (Y = ук)) = Р(Х = хi) Р(Y = ук) для любых допустимых i и к, что легко проверяется, например Р((Х = х1) (Y = у1)) = Р(Х = х1) Р(Y = у1), так как (х3, у1), (х2, у2), (х1, у2), (х3, у2), (х2, у1). Задача 4.Дискретная двумерная случайная величина (
Разыграть случайную величину ( Как и при решении задачи 3, показываем, что информация о независимости случайных величин Задача 5. Дано двузначное число. Число его единиц на 3 меньше числа десятков. Произведение этого числа на число, записанное теми же цифрами в обратном порядке, равно 574. Найдите данное число (Задача №1139 [23]). Ранее с помощью компьютерной программы было показано, что информация в условии "на 3" – лишняя. Приведем другое решение, для чего обозначим через
На основании того, что Приведем еще одно решение, по-видимому, самое простое и изящное. Исключим из условия информацию "на 3". Разложим число 574 на простые множители: 574 = 2∙7∙41= 14∙41. Так как 41 – простое число, то 574 разлагается ровно на два двузначных множителя, каждый из которых содержит одни и те же цифры, записанные в обратном порядке. Теперь очевидно, что в числе 41 число единиц меньше числа десятков. Значит, 41 – искомое число. Отсюда следует, что число его единиц на 3 меньше числа десятков. Итак, информация "на 3" – лишняя Задача 6.Существует ли такое двузначное число, которое при делении на сумму квадратов его цифр даёт в частном 2 и в остатке 6, апри делении на произведение его цифр даёт в частном 4 и остатке 6? (Задача №1064 [24]). Эта задача уже была решена на основе построения соответствующего графика. Теперь приведём другое решение, обозначив через Так как это уравнение равносильно (4х – 1)(5-2у)=7∙1, (22.4) (что легко проверить, раскрыв скобки в этом равенстве, но трудно догадаться, что именно так нужно преобразовать уравнение), причем Следовательно, не существует двузначное число, о котором идёт речь в задаче.
Другие задачи Физическая задача. Скорость автомобиля при торможении выражается формулой v(0)= 18, а = – 1,2 и t = 15, тогда найдем
Поиск по сайту: |
 (21.3)
(21.3) . Ясно, что этот ответ найден в предположении, что все коэффициенты и свободные члены точные, тогда как сама запись: 10,0 и 12,0 свидетельствует, что эти значения приближенные.
. Ясно, что этот ответ найден в предположении, что все коэффициенты и свободные члены точные, тогда как сама запись: 10,0 и 12,0 свидетельствует, что эти значения приближенные.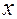 и
и 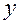 . С этой целью, считая сначала все коэффициенты точными, введем их в ЭВМ, тогда получим:
. С этой целью, считая сначала все коэффициенты точными, введем их в ЭВМ, тогда получим: …
… 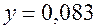 ....
.... ... и
... и 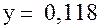 .... Итак, в первом случае результат был
.... Итак, в первом случае результат был 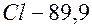 ,
, 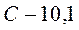 %. Найдите его молекулярную формулу.
%. Найдите его молекулярную формулу.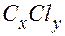 , в которых
, в которых 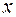 и
и 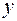 натуральные числа и учитывая процентный состав вещества, запишем уравнение
натуральные числа и учитывая процентный состав вещества, запишем уравнение ,
, – относительная молекулярная масса соединения, значения 12,01 и 35,45 – относительные атомные массы углерода и хлора, соответственно. Поскольку соединение, о котором идет речь, может быть производным как предельного циклического углеводорода, так и предельного углеводорода нециклического строения, то необходимо рассмотреть оба случая. Если предельный углеводород циклический, то в его полностью замещенном производном индексы связаны соотношением
– относительная молекулярная масса соединения, значения 12,01 и 35,45 – относительные атомные массы углерода и хлора, соответственно. Поскольку соединение, о котором идет речь, может быть производным как предельного циклического углеводорода, так и предельного углеводорода нециклического строения, то необходимо рассмотреть оба случая. Если предельный углеводород циклический, то в его полностью замещенном производном индексы связаны соотношением 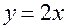 , поэтому, решая два полученных уравнения совместно как систему, найдем
, поэтому, решая два полученных уравнения совместно как систему, найдем 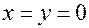 . Значит, неизвестное соединение является производным нециклического углеводорода, поэтому индексы в формуле
. Значит, неизвестное соединение является производным нециклического углеводорода, поэтому индексы в формуле 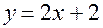 , в котором все коэффициенты точные. Итак, для нахождения целочисленных неизвестных
, в котором все коэффициенты точные. Итак, для нахождения целочисленных неизвестных 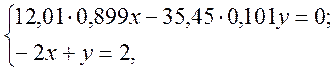 (21.4)
(21.4)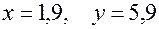 ... Но
... Но 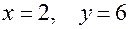 .
.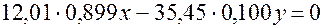 .
.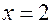 ,
, 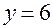 . Тот же результат будем иметь и при замене
. Тот же результат будем иметь и при замене 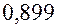 на
на 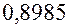 и
и 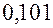 на
на 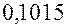 . Итак, решение
. Итак, решение  – молекулярная формула соединения. Кстати, отсюда следует, что
– молекулярная формула соединения. Кстати, отсюда следует, что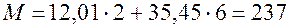 (с точностью до целого).
(с точностью до целого).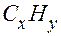 любого углеводорода справедливо неравенство
любого углеводорода справедливо неравенство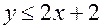 . (22.1)
. (22.1)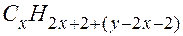 не может быть
не может быть 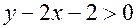 , поскольку в насыщенной структуре, соответствующей формуле алкана
, поскольку в насыщенной структуре, соответствующей формуле алкана 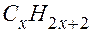 , дополнительным
, дополнительным  атомам водорода места нет. Следовательно,
атомам водорода места нет. Следовательно, 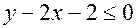 или
или 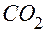 , а остаток составил
, а остаток составил 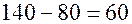 (мл), то углеводород в избытке быть не мог, ибо 40<60. Значит, в избытке был кислород, прореагировавший объем которого составил 200 – 60 = 140 (мл). Обозначив формулу неизвестного углеводорода как
(мл), то углеводород в избытке быть не мог, ибо 40<60. Значит, в избытке был кислород, прореагировавший объем которого составил 200 – 60 = 140 (мл). Обозначив формулу неизвестного углеводорода как 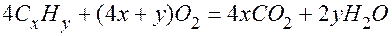 , (22.2)
, (22.2)
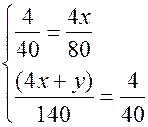 ,
,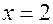 ,
, 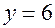 и
и 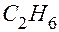 или
или 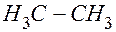 формула углеводорода (этан).
формула углеводорода (этан).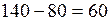 (мл), объем прореагировавшего кислорода
(мл), объем прореагировавшего кислорода 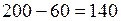 (мл), а образовавшегося углекислого газа
(мл), а образовавшегося углекислого газа  мл, то, записав формулу углеводорода как
мл, то, записав формулу углеводорода как 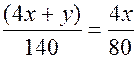 , из которого находим
, из которого находим 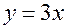 . Но для любого углеводорода
. Но для любого углеводорода  или
или 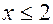 . Однако
. Однако 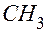 . Значит,
. Значит, 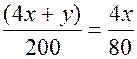 , из которой получаем
, из которой получаем 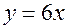 . Но из неравенства (22.1)
. Но из неравенства (22.1) 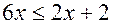 или
или 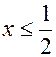 . Но это неравенство не имеет решений во множестве натуральных чисел. Следовательно, не существует углеводород, который мог бы быть в избытке. Значит, в избытке был кислород. Поэтому на основании уравнения реакции (22.2) имеем пропорцию
. Но это неравенство не имеет решений во множестве натуральных чисел. Следовательно, не существует углеводород, который мог бы быть в избытке. Значит, в избытке был кислород. Поэтому на основании уравнения реакции (22.2) имеем пропорцию  , т.е.
, т.е. 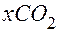 .
.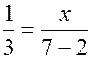 , т. е.
, т. е.  , а это противоречит тому, что
, а это противоречит тому, что 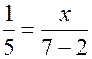 , т. е.
, т. е. 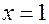 и
и 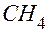 – формула углеводорода (метан). (В соответствии со строением углеводородов с одним атомом углерода соединяются четыре атома водорода).
– формула углеводорода (метан). (В соответствии со строением углеводородов с одним атомом углерода соединяются четыре атома водорода).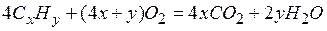 , (22.2)
, (22.2) , из которой находим
, из которой находим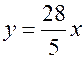 . Теперь из неравенства (22.1)
. Теперь из неравенства (22.1) 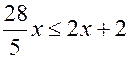 , т.е.
, т.е. 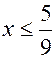 . Следовательно, такого углеводорода нет. Значит, в избытке был кислород. Из уравнения реакции имеем пропорцию
. Следовательно, такого углеводорода нет. Значит, в избытке был кислород. Из уравнения реакции имеем пропорцию 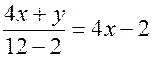 , т.е.
, т.е.  . Но для любого углеводорода
. Но для любого углеводорода 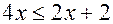 или
или  , т.е.
, т.е. 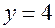 и
и 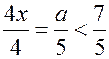 (
( 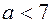 , поскольку в 7 мл входят и углекислый газ, и избыток кислорода). Значит,
, поскольку в 7 мл входят и углекислый газ, и избыток кислорода). Значит,  , а это неравенство имеет единственное решение в целых положительных числах:
, а это неравенство имеет единственное решение в целых положительных числах: 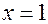 и
и 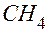 – формула углеводорода.
– формула углеводорода. мл объем кислорода, нужного для сгорания 5 мл углеводорода
мл объем кислорода, нужного для сгорания 5 мл углеводорода 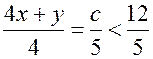
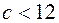 , так как в 12 мл входит и избыток кислорода)
, так как в 12 мл входит и избыток кислорода) ,
,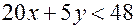 .
. . Подставляя в последнее неравенство вместо у его наименьшее значение, равное 2, получим
. Подставляя в последнее неравенство вместо у его наименьшее значение, равное 2, получим  , а это неравенство имеет в натуральных числах единственное решение
, а это неравенство имеет в натуральных числах единственное решение 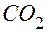 и одного из исходных газов) составил 7 мл, то в этот объем входил и избыток
и одного из исходных газов) составил 7 мл, то в этот объем входил и избыток 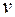 мл одного из исходных газов. Если в избытке был углеводород
мл одного из исходных газов. Если в избытке был углеводород 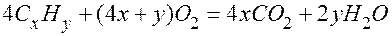 , (22.2)
, (22.2)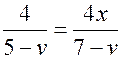 и
и 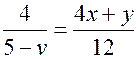 ,
,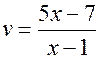 . Подставив найденное значение
. Подставив найденное значение 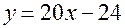 , причем
, причем  , так как при
, так как при  или
или  , т. е.
, т. е.  т.е.
т.е.  ,
,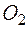 и 250 – 150 = 100 (мл)
и 250 – 150 = 100 (мл) 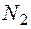 . Теперь запишем формулу углеводорода в виде
. Теперь запишем формулу углеводорода в виде  →
→ 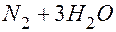 и 2
и 2  . Из первого уравнения следует, что при образовании 100 мл
. Из первого уравнения следует, что при образовании 100 мл 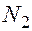 получается 300 мл паров
получается 300 мл паров 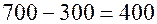 (мл) паров
(мл) паров  , т.е.
, т.е. 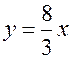 , причем
, причем 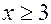 , так как
, так как 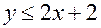 и потому
и потому 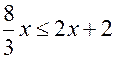 или
или 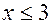 . Значит,
. Значит, 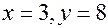 и
и  – формула углеводорода (пропан).
– формула углеводорода (пропан). →
→  (мл) при образовании которых, как следует из уравнения реакции, получается 300 мл паров
(мл) при образовании которых, как следует из уравнения реакции, получается 300 мл паров 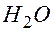 . Значит, при сгорании углеводорода образуется 700 – 300 = 400 (мл) паров воды. Поэтому, с учетом того, что объем
. Значит, при сгорании углеводорода образуется 700 – 300 = 400 (мл) паров воды. Поэтому, с учетом того, что объем  равен 300 мл, из схемы реакции
равен 300 мл, из схемы реакции →
→ 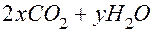 получаем пропорцию
получаем пропорцию 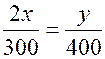 , т.е.
, т.е.  .
.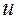 моль
моль 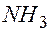 и
и  моль
моль 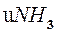 +
+ 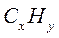 →
→ 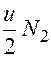 +
+ 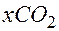 +
+  .
.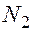 и
и 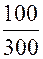 , т.е.
, т.е. 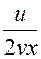 =
=  ,
,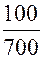 , т.е.
, т.е. 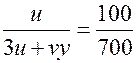 или
или 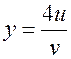 .
.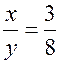 и
и  . Теперь очевидно, что ни бром, ни йод, ни астат не удовлетворяют значению
. Теперь очевидно, что ни бром, ни йод, ни астат не удовлетворяют значению 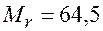 , так как относительная атомная масса каждого из них (80; 127 и 210 соответственно) больше
, так как относительная атомная масса каждого из них (80; 127 и 210 соответственно) больше 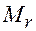 всего галогеналкана. Фтор также не подходит, поскольку его относительная атомная масса с точностью до трёх значащих цифр равна 19,0. Остаётся только хлор, относительная атомная масса которого 35,5 (кстати, это очевидно, поскольку
всего галогеналкана. Фтор также не подходит, поскольку его относительная атомная масса с точностью до трёх значащих цифр равна 19,0. Остаётся только хлор, относительная атомная масса которого 35,5 (кстати, это очевидно, поскольку 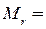 64,5). Значит, молекула галогеналкана содержит один атом хлора, а на остаток, равный 29, приходится два атома углерода и пять атомов водорода (проверка:
64,5). Значит, молекула галогеналкана содержит один атом хлора, а на остаток, равный 29, приходится два атома углерода и пять атомов водорода (проверка: 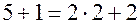 ) и
) и  – молекулярная формула вещества. Возможны и другие варианты.
– молекулярная формула вещества. Возможны и другие варианты. и
и  (
( 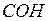 ) = 29, то в его молекуле содержится только одна карбонильная группа
) = 29, то в его молекуле содержится только одна карбонильная группа 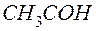 – формула альдегида.
– формула альдегида. , и так как
, и так как 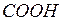 ) = 45, то в молекуле карбоновой кислоты содержится только одна карбоксильная группа. Следовательно, на остаток, равный 60 – 45 = 15 приходится один атом углерода и три атома водорода, а потому
) = 45, то в молекуле карбоновой кислоты содержится только одна карбоксильная группа. Следовательно, на остаток, равный 60 – 45 = 15 приходится один атом углерода и три атома водорода, а потому 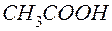 – формула кислоты. Возможны и другие варианты.
– формула кислоты. Возможны и другие варианты.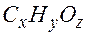 ,где
,где 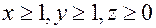 , так как заранее неизвестно входит ли кислород в соединение. Теперь для определения индексов запишем уравнение
, так как заранее неизвестно входит ли кислород в соединение. Теперь для определения индексов запишем уравнение 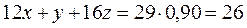 , из которого видно:
, из которого видно: 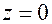 , так как даже при
, так как даже при  и
и  левая часть равенства больше правой. Следовательно, газ – углеводород и
левая часть равенства больше правой. Следовательно, газ – углеводород и 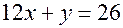 , поэтому
, поэтому 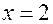 . Но при
. Но при 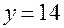 , а углеводорода, формула которого
, а углеводорода, формула которого  не существует. Значит,
не существует. Значит, 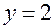 и
и 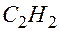 – формула газа (ацетилен).
– формула газа (ацетилен).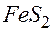 ? [Сергеев С.А. Решения и ответы: К учебнику «Химия. 8–9 класс». – Минск: Изд-во “АРТААЛ – ПРЕСС”, 1997. – С. 150–152].
? [Сергеев С.А. Решения и ответы: К учебнику «Химия. 8–9 класс». – Минск: Изд-во “АРТААЛ – ПРЕСС”, 1997. – С. 150–152]. →
→ 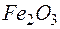 +
+  .
.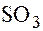 .
.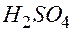 .
.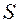 , то, чтобы вычислить массу серной кислоты, которую можно получить из пирита, достаточно воспользоваться схемой
, то, чтобы вычислить массу серной кислоты, которую можно получить из пирита, достаточно воспользоваться схемой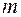 (
( 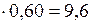 (т), то
(т), то (
( 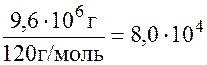 моль.
моль.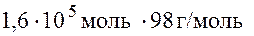 ≈16т.
≈16т. =
=  моль.
моль. =
= 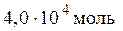 .
.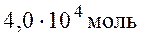
 = 3,92 т.
= 3,92 т.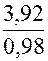 = 4,0 т.
= 4,0 т.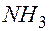 +
+ 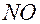 +
+ 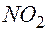
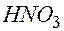 .
. , поэтому в расчетах, относящихся к рассматриваемой задаче, можно пользоваться схемой
, поэтому в расчетах, относящихся к рассматриваемой задаче, можно пользоваться схемой 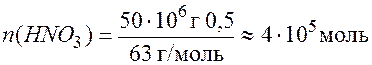 ,
, . Следовательно, потребный объём аммиака при н. у. будет:
. Следовательно, потребный объём аммиака при н. у. будет:
 тыс. м3.
тыс. м3.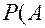
 ) по данным вероятностям:
) по данным вероятностям:  ,
, 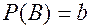 ,
, 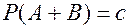 [Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа,1998. – Задача 73].
[Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа,1998. – Задача 73]. = Р(АВ) +
= Р(АВ) + 
 ) и
) и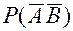 по данным вероятностям:
по данным вероятностям: 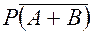 = 1 – Р(А+В)=
= 1 – Р(А+В)=  , т.е. результат не зависит ни от
, т.е. результат не зависит ни от  ), составляющие которой независимы, зная закон её распределения:
), составляющие которой независимы, зная закон её распределения:


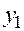
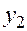
 случайные числа: 0,98; 0,52; 0,01; 0,77; 0,67, а при разыгрывании
случайные числа: 0,98; 0,52; 0,01; 0,77; 0,67, а при разыгрывании 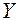 – числа 0,11; 0,80; 0,50; 0,54; 0,31 (там же, задача 715).
– числа 0,11; 0,80; 0,50; 0,54; 0,31 (там же, задача 715).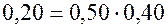 . Значит, информация о независимости
. Значит, информация о независимости 
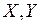 ) (там же, задача 714).
) (там же, задача 714).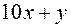 , причем
, причем  – целые неотрицательные числа, для нахождения которых получим смешанную систему:
– целые неотрицательные числа, для нахождения которых получим смешанную систему: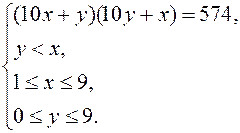
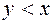 уравнение можно преобразовать в неравенство
уравнение можно преобразовать в неравенство  или
или 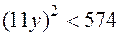 , т.е.
, т.е. 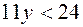 , т.е.
, т.е. 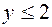 , причем только
, причем только 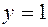 удовлетворяет системе и при этом
удовлетворяет системе и при этом 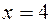 , а потому искомое число равно 41. Кстати, отсюда следует, что число его единиц на 3 меньше числа десятков.
, а потому искомое число равно 41. Кстати, отсюда следует, что число его единиц на 3 меньше числа десятков.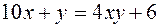 , где
, где 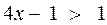 , так как
, так как 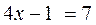 и
и 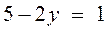 , т.е.
, т.е. 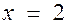 и
и  . Но проверка показывает, что при делении числа 22 на 4 неполное частное равно 5, а не 4, т.е. число 22 не удовлетворяет условию задачи.
. Но проверка показывает, что при делении числа 22 на 4 неполное частное равно 5, а не 4, т.е. число 22 не удовлетворяет условию задачи. . Вычислите путь, пройденный автомобилем, если он остановился через 15 с после начала торможения (путь измеряется в метрах) (Математика в школе, №1, 1989, с. 54 – 55). Из условия задачи исключим число «15» и найдем из уравнения
. Вычислите путь, пройденный автомобилем, если он остановился через 15 с после начала торможения (путь измеряется в метрах) (Математика в школе, №1, 1989, с. 54 – 55). Из условия задачи исключим число «15» и найдем из уравнения  время, через которое после начала торможения автомобиль остановится, тогда получим:
время, через которое после начала торможения автомобиль остановится, тогда получим: 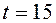 (с). Поскольку производная
(с). Поскольку производная  постоянная и отрицательная (движение при торможении равномерно – замедленное), а потому путь можно вычислить по формуле
постоянная и отрицательная (движение при торможении равномерно – замедленное), а потому путь можно вычислить по формуле  при
при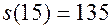 (м). Конечно, этот путь можно вычислить и интегрированием:
(м). Конечно, этот путь можно вычислить и интегрированием: (15) =
(15) =  (м).
(м).