 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ПРИМЕНЕНИЕ ЭВМ К АНАЛИЗУ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
Применение к совершенствованию учебных задач и их Решений
По словам В.И. Феодосьева, приведённым в [29, c. 146]: ЭВМ, «освобождая нас от многих... обязанностей, не освобождает во всяком случае от двух: от необходимости владеть математическим аппаратом и творчески мыслить». Убедимся в этом, решая задачу [13, c. 132 – 133]: Колхоз арендовал два экскаватора. Аренда первого экскаватора стоит 60 руб в день, производительность его в мягком грунте 250 м3 в день, в твердом грунте – 150 м3 в день. Аренда второго экскаватора стоит 50 руб в день, производительность его в мягком грунте 180 м3 в день, а в твердом – 100 м3 в день. Первый работал несколько полных дней и вырыл 720 м3. Второй за несколько полных дней вырыл 330 м3. Сколько дней работал каждый экскаватор, если колхоз заплатил за аренду не более 300 руб.? В этой задаче попытка записать условие в виде системы уравнений и неравенств сталкивается со значительными трудностями, поскольку неизвестно, сколько времени в течение каждого дня экскаваторы работали в твердом и мягком грунтах. Между тем составление всей системы и не нужно. Обозначим через
Рисунок 21.1 – Графическая иллюстрация однозначности решения:
Подчеркнём также, что решение этой задачи с отброшенными данными экономически эффективнее, поскольку для определения производительностей первого и второго экскаваторов в твердом грунте в реальных условиях необходимо затратить средства и время. Прежде чем решать определённого класса химические задачи, построим алгоритм и программу вывода молекулярной формулы углеводорода (МФУ) по заданной величине его относительной молекулярной массы Обозначив МФУ через
Поскольку в молекуле предельного углеводорода
Теперь алгоритм нахождения индексов можно описать так: начиная с Если в результате исполнения алгоритма окажется, что существует только одна пара значений В соответствии с этим алгоритмом запишем на языке бейсик программу МФУ: 10 PRINT "ВВЕДИТЕ М": INPUT M 20 Х = 0 : Z = 0 30 Х=Х+1: Y = M-12*X 40 IF Y< = 0 THEN 70 50 IF Y < = 2*X + 2 THEN Z =Z + 1 : PRINT "X=";X, "Y=";Y 60 GOTO 30 70 IF Z = 0 THEN PRINT "РЕШЕНИЯ НЕТ" 80 IF Z = 1 THEN PRINT "РЕШЕНИЕ ЕДИНСТВЕННОЕ" 90 IF Z > 1 THEN PRINT "РЕШЕНИЕ НЕ ОДНОЗНАЧНОЕ" 100 GOTO 10 110 END
Задача из журнала «Химия в школе». Определите молекулярную формулу углеводорода по следующим данным: при сжигании газообразного углеводорода массой 0,29 г образовались оксид углерода (IV) объёмом 0,448 л и пары воды массой 0,45 г; относительная плотность по водороду данного углеводорода равна 29. Её решение, использующее все данные задачи, приведено в № 6, 1987 г. Отбросив из условия всю информацию, кроме относительной плотности, найдём Рассмотренные здесь и выше решения свидетельствуют о том, что в журналах и учебниках по различным дисциплинам не так уж редко встречаются задачи, в условиях которых содержится данных больше, чем это необходимо для получения результата. Неочевидные лишние данные задачи часто могут быть обнаружены с помощью ЭВМ, в особенности, если решение можно свести к перебору всех возможных вариантов, удовлетворяющих заданным условиям. Для этого сначала составляется и реализуется на ЭВМ программа, использующая все исходные данные. Затем реализуются только части программы соответствующей задачи, из условия которой исключаются те или иные сведения. Если при каком-то варианте исключения данных из непротиворечивой задачи получается тот же результат, что и при всей исходной информации, то такие данные без ущерба для дела можно отбросить и таким образом придать задаче более совершенную формулировку. Таким образом, используя ЭВМ, можно обнаружить в задачах лишние данные, если они имеются, и, исключив их, совершенствовать формулировки задач. Постановка задачи по-новому часто проливает свет на ее подлинное содержание и указывает прямой путь к выбору лучших решений. Задача № 1139 [23]. Дано двузначное число. Число его единиц на 3 меньше числа десятков. Произведение этого числа на число, записанное теми же цифрами в обратном порядке, равно 574. Найдите данное число. Составим программу решения этой задачи и, реализуя её на ЭВМ, найдём, что 41 – искомое число. Теперь исключим из условия информацию "на 3", которую уберем и из программы. Реализуя модифицированную программу, снова получим тот же результат. Следовательно, исключенная информация является лишней. Программа 1.Решение с использованием всех условий: const n=3; р=574; var i,s:integer; begin for i:=3 to 9 do begin if s=p then writeln (′ответ:′,10*i+i-3); end; end. ответ: 41
Программа 2. Решение с исключением информации "на 3": const n=3; р=574; var i,j,s:integer; begin for j:=l to 9 do for i:=0 to j-1 do begin s: =(10*i+j)*(10*j+i) if s=p then writeln('oтвeт: ',10*j+i); end; end. ответ: 41.
Говоря о достоинствах метода математического моделирования в [6, с. 119 – 120], отмечено: «Безусловно, к достоинствам следует отнести тот факт, что модель представляет собой формализованную запись тех или иных законов природы, управляющих функционированием системы, а также гипотез, правдоподобность которых, во всяком случае может быть предметом отдельного рассмотрения. Есть немалое изящество в строгом математическом выводе содержательных высказываний об объекте, если вывод этот сделан из очень ограниченного числа формализованных безусловных утверждений (аксиом). Именно таким изяществом обладают теоремы эвклидовой геометрии, модели теоретической механики и многие другие, ставшие уже классическими». Однако, как уже отмечалось, чтобы почувствовать величие и красоту аксиоматического и связанного с ним дедуктивного метода, вовсе нет необходимости строить такие обширные аксиоматические системы как геометрия Евклида или теоретическая механика. Ведь уже всякую школьную задачу по математике, физике, химии... можно рассматривать как некую аксиоматическую микросистему, в которой роль аксиом играют исходные данные (а также положения и законы других наук, используемые в процессе решения). Иными словами, всё, что дано по условию – это аксиомы, а любые следствия из них, полученные дедуктивно – теоремы. И ещё. В конце одной из моих статей, опубликованной в журнале «Химия и жизнь» [№ 5, 1991, с. 87] , редакция добавила абзац «В заключение – совет: встретив химическую задачу с нагромождением исходных данных, не приступайте сразу к решению, проанализируйте сначала условие задачи. Не исключено, что половина сведений окажется лишней, а после их удаления решение станет гораздо изящней. Ведь, по словам Экзюпери, «совершенство достигается не тогда, когда нечего прибавить, но когда уже ничего нельзя отнять».
Поиск по сайту: |
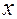 и
и 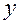 число полных дней, которые работали первый и второй экскаваторы соответственно, тогда получим неравенство, в которое входят оба неизвестных
число полных дней, которые работали первый и второй экскаваторы соответственно, тогда получим неравенство, в которое входят оба неизвестных  или
или 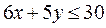 . Первый экскаватор работал не менее трех дней – за два дня, даже в мягком грунте, он вырыл бы всего 500 м3.Точно так же заключаем, что второй экскаватор работал не менее двух дней. Итак,
. Первый экскаватор работал не менее трех дней – за два дня, даже в мягком грунте, он вырыл бы всего 500 м3.Точно так же заключаем, что второй экскаватор работал не менее двух дней. Итак,  . Из компьютерного графика (рисунок 21.1), очевидно, что указанным ограничениям удовлетворяют координаты только одной точки х=3, у = 2. Итак, первый экскаватор работал 3 дня, а второй – два. Заметим, что информация о производительностях экскаваторов в твёрдом грунте в решении не использована, т.е. она лишняя и без ущерба для дела может быть отброшена.
. Из компьютерного графика (рисунок 21.1), очевидно, что указанным ограничениям удовлетворяют координаты только одной точки х=3, у = 2. Итак, первый экскаватор работал 3 дня, а второй – два. Заметим, что информация о производительностях экскаваторов в твёрдом грунте в решении не использована, т.е. она лишняя и без ущерба для дела может быть отброшена.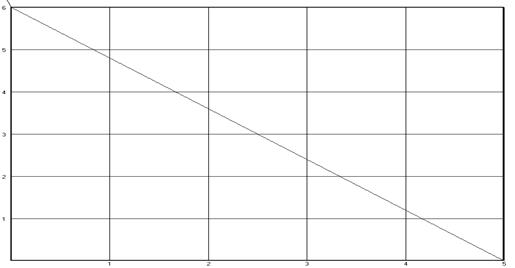
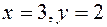
 . При этом относительные атомные массы углерода и водорода считаются равными соответственно 12 и 1 , а величина
. При этом относительные атомные массы углерода и водорода считаются равными соответственно 12 и 1 , а величина 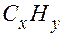 , получим для определения целых положительных чисел
, получим для определения целых положительных чисел  . (21.1)
. (21.1)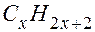 с
с  , для индексов
, для индексов  . (21.2)
. (21.2) и увеличивая каждый раз его значение на 1, вычислять
и увеличивая каждый раз его значение на 1, вычислять 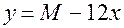 и из каждой пары соответствующих значений
и из каждой пары соответствующих значений 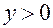 .
.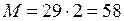 , а исполнив при этом значении М программу, получим однозначный ответ:
, а исполнив при этом значении М программу, получим однозначный ответ:  – МФУ.
– МФУ.