 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ПОНЯТИЕ ОБ ИМИТАЦИОННОМ МОДЕЛИРОВАНИИ
Не для всякого объекта, в частности не для каждой задачи может быть построена адекватная классическая математическая модель. Например, такой задачей будет [13, с. 132]: Сумма, равная 53 коп., составлена из трехкопеечных и пятикопеечных монет, общее число которых меньше 15. Если в этом наборе монет трехкопеечные монеты заменить пятикопеечными, а пятикопеечные – трехкопеечными, то полученная в результате сумма уменьшится по сравнению с первоначальной, но не более, чем в 1,5 раза. Сколько трехкопеечных монет было в наборе? Пусть в наборе было
являющееся компонентом классической математической модели, в которую необходимо включить и два неравенства, соответствующие условию задачи. Но решение указанной смешанной системы, как отмечают авторы книги [13, с. 132], не даст ответа, ибо не все условия задачи можно записать в виде уравнений и неравенств. Поэтому в процессе решения задачи нужны и некоторые рассуждения. Очевидно, равенству (20.1) удовлетворяют лишь те значения у, для каждого из которых число Конечно, для решения уравнения (20.1) в системе координат (рисунок 20.1) с помощью компьютера можно построить график этого уравнения, из которого видно, что он проходит через четыре точки с целочисленными координатами (1; 10), (6; 7), (11; 4) и (16; 1), однако эти наглядные результаты следует проверить непосредственной подстановкой в уравнение указанных координат. Теперь по тексту задачи убеждаемся, что координаты двух последних точек условию задачи не удовлетворяют, поскольку сумма координат каждой из них не меньше 15. Далее, делая проверку, опять - таки по тексту задачи, приходим к выводу, что координаты первой точки условию не удовлетворяют, так как
Рисунок 20.1– Отрезок прямой 3х+5у=53
Подчеркнем: при применении компьютерных графиков к решению задач следует учитывать диапазон изменения координат и в соответствии с ним устанавливать параметры построения. Этим требованиям для последней задачи (рисунок 20.1) удовлетворяют выбранные нами значения параметров: для оси Уже рассмотренный простой пример свидетельствует о том, что не каждую задачу можно решить методом классического математического моделирования. А если задача сложная? Итак, необходим метод исследования сложных систем. И такой метод появился и получил название «имитационное моделирование», что представляет дословный перевод английского «Simulation modeling». Как справедливо отмечено в [6, с. 117] перевод сделан не слишком хорошо, поскольку в нём содержится тавтология. Но ясно одно: имитационное моделирование является обобщением классического математического моделирования. И как математическая модель, так и всякая другая и имитационная модель создается для ответа на вопросы о моделируемом объекте в самом широком смысле. «Суть метода имитационного моделирования состоит в том, что процесс функционирования сложной системы представляется в виде определенного алгоритма, который и реализуется на ЭВМ» [6, с. 118]. Работа с имитационной моделью представляет собой вычислительный эксперимент, обычно осуществляемый на ЭВМ. При построении имитационных моделей так же как и математических, если необходимо, могут формулироваться гипотезы, которые включаются в описание модели. Рассмотрим химическую задачу: При сгорании вещества массой 7,872 г получены оксид углерода IV массой 10,824 г и вода массой 8,856 г. Относительная плотность паров этого вещества по воздуху равна 1,1035. Найти молекулярную формулу вещества. Исключим из условия всю количественную информацию, кроме плотности, да и ее округлим до 1,10, тогда Из условия переформулированной задачи следует, что вещество может содержать кислород. Предположим (гипотеза), что кислород не входит в состав соединения, т.е. оно углеводород, формулу которого запишем в виде
Рисунок 20.2– Пересечение графиков функций:
И теперь подчеркнём: рассмотренная в начале этого параграфа простая учебная задача показывает, что имитационная модель может выступать в роли лаборатории, в которой анализируются элементы некоторых множеств, часть из которых отсеивается, а часть остается для дальнейшего использования. А вот как характеризует имитационное моделирование Е.С. Вентцель [3, c. 146]:«Оно применяется к процессам, в ход которых может время от времени вмешиваться человеческая воля. Человек … может, в зависимости от сложившейся обстановки, принимать те или другие решения, подобно тому, как шахматист, глядя на доску, выбирает свой очередной ход. Затем приводится вдействие математическая модель, которая показывает, какое ожидается изменение обстановки в ответ на это решение и к каким последствиям оно приведет… Следующее «текущее решение» принимается уже с учетом реальной новой обстановки и т. д. В результате многократного повторения такой процедуры руководитель как бы «набирает опыт» … и постепенно выучивается принимать правильные решения…» Опишем имитационную модель решения задачи: Установить молекулярную формулу углеводорода, относительная молекулярная масса которого равна 30. Сначала построим математическую модель, которую затем включим в имитационную модель, как, более общую. Обозначив через А так характеризуется имитационное моделирование в [29, c. 140]: «Разновидностью вычислительного эксперимента является так называемое имитационное моделирование, применяемое для анализа поведения сложных экономических и т. п. задач, для которых математическую модель в виде системы уравнений даже выписать затруднительно». Теперь укажем один из способов решения задачи, встречающейся в школьных учебниках математики и информатики: Найти наибольший общий делитель (НОД) двух натуральных чисел НОД ( НОД ( и описанную с помощью алгоритма последовательного вычитания: 1) если числа равны, то взять любое из них в качестве ответа, в противном случае продолжить выполнение алгоритма; 2) определить большее из чисел; 3) заменить большее число разностью большего и меньшего из чисел; 4) перейти к пункту 1). Этот алгоритм, известный под названием алгоритма Евклида, состоит из отдельных команд, каждая из которых представляет простое действие. Его особенность состоит в том, что все действия, указанные в алгоритме, могут повторяться многократно. Величина разности между большим и меньшим из чисел, фигурирующих в алгоритме, с каждым новым вычитанием уменьшается, а потому после конечного числа повторений, сравниваемые числа обязательно станут равными. Этот алгоритм применим к любым натуральным числам, и всегда за конечное число шагов приводит к решению поставленной задачи, но является трудоёмким, хотя именно он приводится в пособии для средних учебных заведений «Основы информатики и вычислительной техники» под редакцией А.П. Ершова и В.М. Монахова. Заканчивая этот параграф отметим, что в большинстве случаев практически более выгодным для отыскания НОД двух натуральных чисел является другой алгоритм Евклида, основанный на методе последовательного деления [40, c. 31], а для небольших чисел чаще всего используется способ разложения их на простые множители с последующим составлением из таких множителей по хорошо известным правилам НОД данных чисел. Если НОД нескольких натуральных чисел равно 1, то такие числа называются взаимно простыми. …ЭВМ, проникшие сейчас в самые разнообразные области деятельности, были впервые созданы именно для «обслуживания» математических моделей. А.Д. Мышкис
Поиск по сайту: |
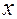 трехкопеечных монет и
трехкопеечных монет и 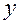 – пятикопеечных, тогда имеет место уравнение
– пятикопеечных, тогда имеет место уравнение , (20.1)
, (20.1)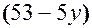 делится на 3, а это условие и нельзя записать в виде уравнения или неравенства. Однако перебор всех возможных значений натуральных чисел
делится на 3, а это условие и нельзя записать в виде уравнения или неравенства. Однако перебор всех возможных значений натуральных чисел 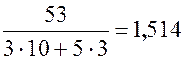 , что больше 1,5 и только координаты точки (6; 7) удовлетворяют всем условиям задачи. Следовательно, в первоначальном наборе было 6 трехкопеечных монет.
, что больше 1,5 и только координаты точки (6; 7) удовлетворяют всем условиям задачи. Следовательно, в первоначальном наборе было 6 трехкопеечных монет.
 (0: 20), оси
(0: 20), оси  (0:10), количество вертикальных линий – 20, количество горизонтальных линий – 10. Поскольку в рассмотренной задаче переменные
(0:10), количество вертикальных линий – 20, количество горизонтальных линий – 10. Поскольку в рассмотренной задаче переменные  .
. , тогда для определения неизвестных индексов получим систему:
, тогда для определения неизвестных индексов получим систему:  и
и  . Построив с помощью компьютера графики функций
. Построив с помощью компьютера графики функций  и
и 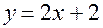 (рисунок 20.2) увидим, что эта система в натуральных числах решений не имеет, т.е. гипотеза неверна. Следовательно, вещество, о котором идет речь в задаче, содержит кислород. Поскольку оно состоит из углерода, водорода и кислорода, в его молекуле будет только один атом кислорода, на который приходится 16 единиц из 32, а тогда на оставшиеся 16 единиц могут приходиться только один атом углерода и 4 атома водорода. Значит,
(рисунок 20.2) увидим, что эта система в натуральных числах решений не имеет, т.е. гипотеза неверна. Следовательно, вещество, о котором идет речь в задаче, содержит кислород. Поскольку оно состоит из углерода, водорода и кислорода, в его молекуле будет только один атом кислорода, на который приходится 16 единиц из 32, а тогда на оставшиеся 16 единиц могут приходиться только один атом углерода и 4 атома водорода. Значит, 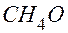 – его молекулярная формула.
– его молекулярная формула.
 и
и 
 , построим для определения неизвестных индексов математическую модель:
, построим для определения неизвестных индексов математическую модель:  , где
, где  , тогда из уравнения
, тогда из уравнения  , но из-за несоответствия валентностей такого углеводорода нет. На основе математической модели принимаем следующее «текущее решение»
, но из-за несоответствия валентностей такого углеводорода нет. На основе математической модели принимаем следующее «текущее решение» 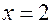 , но тогда из уравнения следует, что
, но тогда из уравнения следует, что  . Очевидно, не может быть
. Очевидно, не может быть  , следовательно,
, следовательно,  – молекулярная формула углеводорода. Таким образом, имитационная модель обобщает математическую и может быть описана с помощью алгоритма, содержащего математическую модель и соответствующие команды информатики (например, ветвления или повторения).
– молекулярная формула углеводорода. Таким образом, имитационная модель обобщает математическую и может быть описана с помощью алгоритма, содержащего математическую модель и соответствующие команды информатики (например, ветвления или повторения). и
и 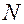 .
. и
и  ) невозможно записать в виде формулы, т.е. для его нахождения нельзя построить классическую математическую модель, но можно создать имитационную модель, основанную на том свойстве, что если
) невозможно записать в виде формулы, т.е. для его нахождения нельзя построить классическую математическую модель, но можно создать имитационную модель, основанную на том свойстве, что если