 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
О понятии «вероятность события»
Известно, что простейшие закономерности естествознания описываются одной из двух схем: 1) если осуществляется комплекс условий 2) если осуществляется комплекс условий В первом случае событие Например, все теоремы математики могут быть сформулированы в виде схемы 1. Однако гораздо чаще мы сталкиваемся с такой ситуацией, в которой событие Когда спортсмен стреляет в мишень, то при выстреле может произойти попадание или промах при одном и том же комплексе условий (одна и та же мишень, тот же стрелок, одно и то же расстояние до мишени, та же винтовка и т. д.). Возникает вопрос: означает ли случайность события Пусть, например, установлено, что спортсмен при данных условиях стрельбы дает 80 % попаданий. Это означает, что из сотни выстрелов, произведенных им при указанных выше условиях, в среднемон попадет 80 раз и значит, 20 – промахнется и в среднемпри многократном повторении стрельбы в тех же условиях этот процент попаданий будет оставаться неизменным, пока с течением времени не произойдет каких-нибудь существенных изменений, при которых стрелок повысит или понизит свою квалификацию. Опыт показывает, что у такого стрелка 80 % попаданий служит показателем его мастерства, и этот процент оказывается устойчивым,т.е. в большинстве стрельб в тех же условиях результат будет для данного стрелка почти один и тот же, лишь в редких случаях уклоняясь сколько-нибудь значительно от своего среднего значения. Приведём другой пример. На некотором предприятии было замечено, что в данных условиях в среднем 1,5 % изготовленных изделий оказываются не удовлетворяющими стандарту и идут в брак. Это означает, что в партии, скажем, из 1000 изделий, еще не подвергнутых браковке, будет примерно 15 непригодных. Иногда, конечно, число бракованных изделий может оказаться несколько больше, иногда несколько меньше, но в среднем это число будет близко к 15. Конечно, и здесь предполагается, что условия производства (организация технологического процесса, оборудование, сырье, квалификация рабочих и пр.) остаются неизменными. Таких примеров, когда комплекс условий неоднозначно определяет результат, можно привести сколько угодно. Во всех этих примерах мы видим, что при однородных массовыхоперациях (многократная стрельба, массовое производство изделий и т. п.) процент того или другого вида важных для нас событий при данных условиях почти всегда бывает примерно одним и тем же. Можно поэтому сказать, что этот средний процент является характерным показателем соответствующей массовой операции при данных условиях. Процент попадания описывает нам мастерство стрелка, процент брака или лучше сказать процент стандартных изделий оценивает доброкачественность продукции. Знание таких показателей очень важно в самых различных областях техники, экономики, физики, химии и пр.; оно позволяет нам не только оценивать уже происшедшие массовые операции, но и предвидеть их исходы в будущем. Если спортсмен в данных условиях стрельбы попадает в мишень в среднем 80 раз из 100 выстрелов, то мы говорим, что для этого спортсмена в указанных условиях относительная частота попаданиясоставляет 80 % или 0,80. Вообще, если событие Пусть, например, в процессе подбрасывания монеты Такой же ответ мы получим, если воспользуемся классическим определением вероятности выпадения герба. В классической схеме При построении стохастических моделей задач не так уж редко применяется и геометрическое определение вероятности события
Поиск по сайту: |
 , то наступает событие
, то наступает событие  ;
; , то событие
, то событие  в серии из
в серии из 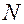 независимых испытаний появилось
независимых испытаний появилось  раз, то отношение
раз, то отношение  называется относительной частотой этого события в серии из
называется относительной частотой этого события в серии из 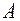 и обозначается
и обозначается  . Вероятность события – это идеализированная, теоретическая его частота (относительная). Итак,
. Вероятность события – это идеализированная, теоретическая его частота (относительная). Итак, 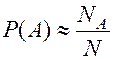 при больших значениях
при больших значениях  , а отношение
, а отношение  будет близким к
будет близким к  , и потому можно считать экспериментально установленным, что в рассматриваемом процессе
, и потому можно считать экспериментально установленным, что в рассматриваемом процессе  , т.е. это число – вероятность события
, т.е. это число – вероятность события  «выпадение герба».
«выпадение герба».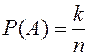 , где
, где  – общее число всех равновозможных и несовместных исходов опыта, из которых «
– общее число всех равновозможных и несовместных исходов опыта, из которых « 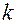 » соответствуют (благоприятствуют) событию
» соответствуют (благоприятствуют) событию  и
и