 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ЭВМ – соавтор открытия
Ярким примером удачного применения вычислительного эксперимента в физике было открытие Т-слоя (Теплового слоя). Его суть состоит в том, что в плазме, взаимодействующей с магнитным полем, при определенных условиях возникают слои высокой температуры. Как отмечает академик А. А. Самарский [36, c. 45]: «Т-слой был открыт с помощью вычислительных экспериментов. С высокой точностью были описаны условия, при которых должен возникать неизвестный прежде эффект. Физические эксперименты, в которых он мог бы появиться, тогда еще не ставились в силу их сложности. Это породило борьбу мнений, вызвало недоверие со стороны некоторых ученых, занимающихся исследованиями плазмы, – уж очень необычная была ситуация: физический эффект открыт математиками. Между тем, получив от математиков точное описание нового эффекта, физики взялись обнаружить его экспериментально. Три различных научных коллектива Москвы, Новосибирска и Сухуми, независимо друг от друга на различных установках зарегистрировали Т-слой». Соавтором нового физического открытия стала ЭВМ. Итак, вычислительный эксперимент – это современная технология и методология проведения различных исследований. Его основой является математическая модель, теоретической базой – вычислительная математика, а технической – компьютеры. О ПЛАНИРОВАНИИ ЭКСПЕРИМЕНТА Планирование эксперимента — комплекс мероприятий, включающих и минимизацию общего числа опытов, необходимых для решения поставленной задачи. Задачи, для решения которых может использоваться планирование эксперимента, разнообразны. Можно сказать, что там, где есть эксперимент, возникает и вопрос о его планировании. Так, для непосредственного измерения площади комнаты прямоугольной формы, необходимо в качестве единиц измерения иметь, например, наборы квадратных плиток площадью 1м2, 1дм2, 1см2, которыми можно покрыть весь пол, а затем, пересчитав их, выразить результат в квадратных метрах. Как видим, прямое измерение площади фигуры даже в виде прямоугольника представляет непростую задачу в особенности, если нужно найти площадь большого сельскохозяйственного поля. Поэтому эксперимент по определению площади естественно спланировать так, чтобы упростить, сократить его, непосредственно измеряя вместо площади длины сторон прямоугольника, и по ним найти площадь. Итак, если нужно определить площадь пола комнаты прямоугольной формы, то для этого пол считают прямоугольником, измеряют его длину и ширину, а затем перемножают полученные числа. Вот этот прямоугольник идеализированный, математический вместе с его параметрами: a – длиной, b - шириной, формулой для вычисления площади: s = a∙b и есть всем известная математическая модель (ММ) рассматриваемой задачи, позволяющая по линейным размерам косвенно определить, измерить площадь. Таким образом, с ММ связано одно существенное свойство: её участие в эксперименте, в его планировании. В этой связи укажем, что преподаватель американского колледжа смотрел у себя дома по телевизору высадку астронавтов на Луну. Он заметил, что из одного отсека корабля свисал, качаясь на чем-то вроде каната, какой-то тяжелый предмет. Тогда у преподавателя и возник план эксперимента по измерению ускорения силы тяжести на поверхности Луны с помощью телевизора. Если измерить на экране Т (телевизора) длины отрезков, соответствующие росту астронавта В средствах массовой информации не раз возникал вопрос «А были ли американские астронавты на Луне?» Уж много явных несуразиц имеется на кадрах «лунной хроники». В частности, в газете «Слава Севастополя» от 29 ноября 2003 г. («высадка на Луну снималась в Голливуде») появилось со ссылкой на соответствующие источники сообщение, что вдова кинорежиссёра Стэнли Кубрика поведала экстраординарную историю: кадры высадки американских астронавтов на Луну массово фальсифицировались умельцами из Голливуда, а решение о фальсификации принималось лично президентом США. В газете подчёркнуто: «Под сомнение поставлен не только приоритет Америки в освоении Луны, но и её моральная чистоплотность – и последнее может иметь далеко идущие последствия, если сказанное вдовой Стэнли Кубрика окажется правдой». Если бы высадка на Луну фальсифицировалась съёмкой фильма на земле, то найденное таким указанным способом ускорение составило бы 9,8 м/c2. Этот элементарный расчет не только опровергает домыслы вдовы Стэнли Кубрика о фальсификации высадки американских астронавтов на Луну, но и подтверждает их пребывание на ней. Отклик И. Ковалевой и А. Хрусталева на указанную в «Славе Севастополя» статью опубликован в той же газете от 10 декабря 2003 года под заголовком «Миф или правда?». Конечно, съёмки фильма о высадке астронавтов на Луну проводились на Земле, но это не значит, что астронавты не были на Луне. С помощью законов природы зависимости между величинами, выражающими отдельные факторы из условий задачи, формулируются как математические модели – часто в виде арифметических соотношений или уравнений. Конкретное использование таких моделей позволяет не только решать задачи, но и совершенствовать их формулировки. Задача 1 (из журнала «Химия в школе»).При сгорании вещества массой 7,872 г получены оксид углерода IV массой 10,824 г и вода массой 8,856 г. Относительная плотность паров этого вещества по воздуху равна 1,1035. Найти молекулярную формулу вещества. В формулировке этой задачи точности исходных количественных данных чрезмерны: каждое содержит не менее четырех значащих цифр. Если учесть, что в реальных условиях их получают экспериментально, то для таких значений необходимы высокоточные измерения, на которые затрачиваются неоправданные средства и время. Именно поэтому эксперименты необходимо планировать. При выводе молекулярной формулы вещества целесообразно сначала измерить величины, на основе которых определяется относительная молекулярная масса (ОММ) вещества и по ней с помощью соответствующего алгоритма перебора решить задачу. В соответствии с этим планом отбросим все числовые значения, кроме плотности, да и её округлим до трех значащих цифр, т.е. будем решать задачу: Найти молекулярную формулу вещества, относительная плотность паров которого по воздуху равна 1,10, если при его сжигании образуется оксид углерода и вода. Поскольку при сгорании вещества образуется оксид углерода, пусть даже неизвестно какой, и вода, в соединение входит углерод, водород и возможно кислород. С точностью до целого ОММ соединения Мr = 32 (1,10∙29 » 32). Предположим, что вещество – углеводород. Тогда очевидно в его молекуле может быть либо один атом углерода, либо 2. Но эти случаи невозможны, так нет углеводородов, формулы которых СН20 или С2Н8. Значит, в молекулу соединения входит кислород, причем один атом, а тогда на оставшиеся 16 единиц ОММ может приходиться только один атом углерода и 4 атома водорода. Следовательно, СН4О – молекулярная формула вещества. Теперь рассмотрим вопросы, связанные с планированием экспериментов с моделями молекул, которые позволяют определять межъядерные расстояния в молекулах и валентные углы с помощью измерений. Такой подход возможен потому, что в основу геометрии молекул положено представление о молекуле как о системе атомов, имеющей в нормальном состоянии определённую конфигурацию. Конкретные значения межъядерных расстояний в молекуле могут быть получены, например, с помощью электронографического эксперимента. Между линейными и угловыми элементами геометрии молекул существуют определенные зависимости. Это дает возможность в удобном масштабе с помощью циркуля, линейки и транспортира строить соответствующие подобные треугольники, неизвестные длины сторон и углы которых могут быть измерены с помощью указанных инструментов. Химическая задача.В учебниках химии отмечается, что модель молекулы метана СH4 –тетраэдрическая (рисунок 15.1), т.е. как геометрическая фигура является правильным тетраэдром, но при этом величина валентного угла Н–С–Н, равная ≈ 109,5º, например, в школьном учебнике сообщается догматически.
Найдем величину этого валентного угла измерением на основе подобия правильных тетраэдров. Для этого построим модель молекулы метана в виде правильного тетраэдра, в вершинах и центре О которого (рисунок 15.1) укажем в круглых скобках символы соответствующих элементов A(Н), В(Н), D(H), S(H), О(С). Так как точка О – центр правильного тетраэдра Построим правильный треугольник ABD (рисунок 15.2). За его сторонувозьмем отрезок а, удобный для построения. С помощью точки пересечения двух серединных перпендикуляров к сторонам ∆ABD находим его центр
Конечно, осветить все вопросы, связанные с планированием эксперимента невозможно. Эта тема неисчерпаема. Именно поэтому мы поставили заголовок «О планировании …».
Высшее назначение математики … состоит в том, чтобы находить скрытый порядок в хаосе, который нас окружает. Н. Винер
Поиск по сайту: |
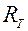 и подвесу маятника
и подвесу маятника 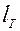 в вертикальном положении, то зная истинный рост астронавта R и обозначив истинную длину подвеса через
в вертикальном положении, то зная истинный рост астронавта R и обозначив истинную длину подвеса через 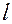 можнона основании подобия записать пропорцию
можнона основании подобия записать пропорцию 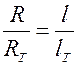 , откуда
, откуда  . Подставив в последнюю формулу известные значения величин, находящихся в её правой части, был найден результат:
. Подставив в последнюю формулу известные значения величин, находящихся в её правой части, был найден результат: 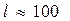 (см). Период колебаний, за которыми следил преподаватель, он определил по секундной стрелке часов: 5 с. Отсюда, пользуясь формулой для периода колебаний маятника
(см). Период колебаний, за которыми следил преподаватель, он определил по секундной стрелке часов: 5 с. Отсюда, пользуясь формулой для периода колебаний маятника 
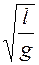 , можно оценить и ускорение силы тяжести на поверхности Луны: g
, можно оценить и ускорение силы тяжести на поверхности Луны: g 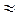 160 см/с2. Эта величина составляет
160 см/с2. Эта величина составляет  ускорения силы тяжести на поверхности Земли. Так, не выходя из дому, с помощью телевизора и принципа подобия был произведён настоящий «космический» эксперимент.
ускорения силы тяжести на поверхности Земли. Так, не выходя из дому, с помощью телевизора и принципа подобия был произведён настоящий «космический» эксперимент.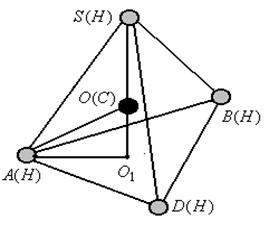 Рисунок 15.1
Рисунок 15.1
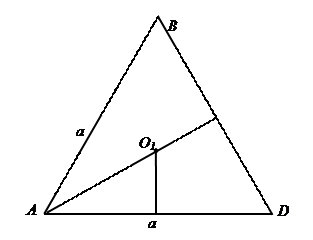 Рисунок 15.2
Рисунок 15.2
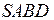 , т.е. центр описанной около него сферы
, т.е. центр описанной около него сферы 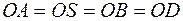 . Обозначим через а длину ребра тетраэдра и продолжим SO до пересечения с основанием
. Обозначим через а длину ребра тетраэдра и продолжим SO до пересечения с основанием  . Тогда
. Тогда 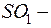 высота,
высота, 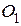 – центр правильного треугольника со стороной а.
– центр правильного треугольника со стороной а.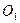 .
. Теперь строим прямоугольный треугольник (рисунок 15.3) по гипотенузе а и построенному на рисунке 2 отрезку АО1 – катету ∆АО1S. Затем строим с помощью циркуля угол SАО равный углу АSО1, сторона АО которого заканчивается в точке О – центре тетраэдра. Если измерить угол АОS транспортиром, цена деления угломерной шкалы которого 0,5°, найдем его величину ≈109,5º, которая равна величине валентного угла
Теперь строим прямоугольный треугольник (рисунок 15.3) по гипотенузе а и построенному на рисунке 2 отрезку АО1 – катету ∆АО1S. Затем строим с помощью циркуля угол SАО равный углу АSО1, сторона АО которого заканчивается в точке О – центре тетраэдра. Если измерить угол АОS транспортиром, цена деления угломерной шкалы которого 0,5°, найдем его величину ≈109,5º, которая равна величине валентного угла