 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Применение метода к решению невероятностных задач
1) Найти Решение: Рассмотрим интеграл вида
явно выделив в качестве множителя в подынтегральном выражении единицу, которая будет играть роль плотности распределения:
Но тогда выражение (17.1) будет математическим ожиданием случайной величины х, равномерно распределенной в интервале
Математическое ожидание можно оценить средним арифметическим наблюдаемых значений случайной величины:
Возьмем Итак, просматривая последние цифры 16 номеров телефонов, выпишем их последовательность, например, полученную в нашем эксперименте: 6; 9; 3; 1; 5; 3; 8; 4; 7; 6; 0; 2; 4; 7; 8; 9. Так как каждое случайное число должно принадлежать интервалу (Ответ записан с точностью до одной значащей цифры) Точное значение этого интеграла равно 0,5, так как
2) Исходя из вероятностных представлений, вычислить число π. Рассмотрим квадрат со стороной, равной единице, и четверть круга в нем (рисунок 17.2). Тогда геометрическая вероятность попадания случайной величины в четверть круга, площадь которого
(0,6; 0,9), (0,3; 0,1), (0,5; 0,3), (0,8; 0,4), (0,7; 0,6), (0; 0,2), (0,4; 0,7), (0,8; 0,9).
В нашем эксперименте
Рисунок 17.2 – Пояснение к экспериментальному определению числа
Не менее полезно проведение натурных экспериментов, которые позволяют убедиться в том, что модельные результаты согласуются с данными опытов. Сравним, например вероятность выпадения герба и цифры при подбрасывании двух монет с её эмпирическим аналогом – относительной частотой, определяемой экспериментально. Теоретическая, идеализированная частота, т.е. вероятность, в этом случае равна 0,5. Экспериментальное решение можно получить так: каждый слушатель из группы, например в 25 человек, десять раз подбрасывает две монеты, и регистрирует, сколько раз выпали герб и цифра. Всего, таким образом, будет проведено 250 опытов, примерно в половине которых выпадет герб и цифра, а потому относительная частота указанного события 0,5. В этой связи заметим, что Даламбер, как пишут в некоторых книгах, считал: при подбрасывании двух монет три события – выпадение двух гербов, двух цифр, а также одного герба и одной цифры – равновозможны. Если бы это было так, то относительная частота выпадения герба и цифры равнялась бы примерно О сущности метода Сущность метода Монте–Карло состоит в том, что искомая величина представляется в виде математического ожидания некоторой случайной величины, математическое ожидание которой заменяется средним арифметическим реализаций этой случайной величины при большом числе испытаний, обычно проводимых на ЭВМ. При этом оценка погрешности метода сводится к интервальной оценке погрешности математического ожидания. Особенностью метода является простая структура вычислительного алгоритма, в соответствии с которым составляется программа для проведения одного испытания, которое затем многократно повторяется. Именно поэтому метод Монте-Карло называют еще и методом статистических испытаний. Есть одна наука, без которой невозможна никакая другая. Это математика. Ее понятия, представления и символы служат тем языком, на котором говорят, пишут и думают другие науки. С.Л. Соболев § 18. ПРОСТЕЙШИЕ ТЕОРЕМЫ МАТЕМАТИЧЕСКОЙ ХИМИИ И ИХ ПРИЛОЖЕНИЯ К РЕШЕНИЮ ЗАДАЧ Как уже отмечалось, математика проникла во все области знания. Давно стали классическими такие научные и учебные дисциплины как математическая физика и математическая статистика. В ХХ веке появилось множество новых названий: математическая экономика, математическая лингвистика, математическая психология и т.д. И какую бы науку ни взять, теперь вряд ли кому-нибудь покажется невозможным присоединение к её наименованию эпитета «математическая». Что же касается «Математической химии», то такое словосочетание, по-видимому, впервые применено в работе М.В. Ломоносова «Элементы математической химии» (1741г.). Теперь математика применяется не только как средство решения задач, но и, что ещё важнее, как способ формулирования химических законов и закономерностей.
Поиск по сайту: |

 , исходя из вероятностных представлений.
, исходя из вероятностных представлений. , (17.1),
, (17.1), .
.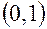 :
: .
. .
. (малая выборка) и воспользуемся телефонным справочником для получения случайных чисел (берем последние цифры). Так как у нас интервал
(малая выборка) и воспользуемся телефонным справочником для получения случайных чисел (берем последние цифры). Так как у нас интервал 

 =
=  =0,5.
=0,5.
 будет
будет  , где
, где  и
и  — число случайных точек попадания в четверть круга и в квадрат соответственно. Отсюда
— число случайных точек попадания в четверть круга и в квадрат соответственно. Отсюда  . Как и при решении предыдущей задачи для определения
. Как и при решении предыдущей задачи для определения  ,
,  . Следовательно,
. Следовательно,  .
.
 .
. . Но как было отмечено выше, относительная частота выпадения герба и цифры, получаемая на основе опыта близка к 0,5. Таким образом, гипотеза Даламбера неверна. (Правда, трудно поверить, чтобы он мог её высказать).
. Но как было отмечено выше, относительная частота выпадения герба и цифры, получаемая на основе опыта близка к 0,5. Таким образом, гипотеза Даламбера неверна. (Правда, трудно поверить, чтобы он мог её высказать).