 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
К построению математических моделей задач
Первая основана на определении определённого интеграла как предела интегральной суммы. При этом искомая величина приближённо представляется в виде интегральной суммы с последующим предельным переходом как при вычислении площади криволинейной трапеции. При применении второй схемы предполагается существование такой дифференцируемой функции, на основании которой определяется искомая величина, для чего из условия задачи находится дифференциал (или производная) этой функции и вычислением определённого интеграла получается значение искомой величины. Подчеркнём, что в этой схеме сначала выдвигается гипотеза о существовании указанной функции, однако эта нестрогость не имеет значения, так как в каждой конкретной задаче мы эту функцию фактически находим и тем самым убеждаемся в справедливости выдвинутой гипотезы. Задача 1. a) Определить работу, необходимую для запуска ракеты весом b) Определить работу, которую должен совершить двигатель, чтобы полностью освободить ракету от земного притяжения. При решении землю и ракету примем за материальные точки с соответствующими массами. По закону всемирного тяготения
Рисунок 12.2 – Модель сечения Земли
Теперь ясно, что для определения работы, которую должен совершить двигатель, чтобы полностью освободить ракету от земного притяжения, необходимо в интеграле (12.2) перейти к пределу при
Итак, работа оказалась конечной величиной, а несобственный интеграл с бесконечным пределом здесь представляет математическую модель, адекватно отражающую объективную действительность. Задача 2. Тело массой m совершает вдоль прямой горизонтальные колебания под действием пружины. Найти период колебаний этого тела, пренебрегая массой пружины, трением и сопротивлением среды. Решение: ось х направим вдоль прямой колебаний, а начало координат поместим в точке равновесия (рисунок 12.3).
Рисунок 12.3 – Пружинный маятник
Для определения периода колебаний отклоним материальную точку (модель тела)
Сейчас для нас важно, что знаменатель
v = –
Здесь перед корнем поставлен знак минус, так как 0 < x < x0 (проекция скорости на ось С помощью законов природы зависимости величин, выражающих отдельные факторы изучаемого явления, формулируются в виде уравнений, как правило, дифференциальных… А.А.Самарский
Поиск по сайту: |
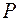 с поверхности земли на высоту
с поверхности земли на высоту  (рисунок 12.2).
(рисунок 12.2).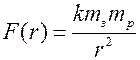 , где
, где 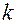 – коэффициент пропорциональности,
– коэффициент пропорциональности,  – масса земли,
– масса земли,  – масса ракеты,
– масса ракеты, 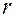 – расстояние между материальными точками, моделирующими землю и ракету. Так как на поверхности земли радиуса
– расстояние между материальными точками, моделирующими землю и ракету. Так как на поверхности земли радиуса 
 и
и  , то
, то  и
и  . Обозначим через
. Обозначим через  работу, которую совершает двигатель ракеты при
работу, которую совершает двигатель ракеты при  , тогда
, тогда  и работа на пути от
и работа на пути от  будет равна
будет равна . (12.2)
. (12.2)
 . (12.3)
. (12.3)
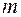 вправо на расстояние
вправо на расстояние  и отпустим при
и отпустим при  . Поскольку
. Поскольку  , период колебаний будет
, период колебаний будет (12.4)
(12.4) подынтегральной функции при
подынтегральной функции при  равен нулю, т. е. правая часть (12.4) является несобственным интегралом от неограниченной функции, но этот интеграл представляет собой математическую модель реальной величины – периода колебаний. Проще всего найти этот интеграл, используя физический закон сохранения энергии
равен нулю, т. е. правая часть (12.4) является несобственным интегралом от неограниченной функции, но этот интеграл представляет собой математическую модель реальной величины – периода колебаний. Проще всего найти этот интеграл, используя физический закон сохранения энергии , из которого имеем:
, из которого имеем:
 ,
,
 при
при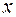 – отрицательная, поскольку точка движется влево)
– отрицательная, поскольку точка движется влево)