 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
На основании подобия треугольников можно решать различные задачи, связанные с определением расстояний, измерить которые непосредственно либо сложно, либо невозможно.
В современной теории подобия достаточные признаки подобия формулируются с помощью безразмерных комплексов величин, представляющих собой произведение степеней этих величин, называемых критериями подобия. Рассмотрим этот вопрос в связи с геометрическим подобием фигур. Для этого заметим, что всякий объект может быть задан однозначно определяющими его параметрами. Например, круг однозначно определяется радиусом, треугольник тремя сторонами, двумя сторонами и углом между ними и т. п. Еще раз подчеркнем, что в подобных фигурах отношения длин соответствующих (сходственных) линейных элементов не изменяются! Именно эта неизменность отношений жестко связана с постоянством углов между соответствующими отрезками подобных фигур, что позволяет измерять углы отвлеченными числами, равными отношениям длин линейных элементов тех фигур, которым принадлежат углы. Итак, построим угол с вершиной в точке О (рисунок 10.3) и проведем две любые дуги разного радиуса от одной стороны этого угла до другой. Так как оба образовавшиеся секторы подобны, то отношение длины дуги к длине соответствующего радиуса будет одинаковым и постоянным для данного угла. Это значит, что указанное отношение, т.е. число, однозначно определяет величину угла. Следовательно, этим числом можно измерять его величину. Такая мера угла, как известно, называется радианной. Из рисунка 10.3 имеем:
Рисунок 10.3 – Радианная мера угла Рассмотрим треугольник, определяемый двумя сторонами и углом между ними (рисунок 10.4).
Рисунок 10.4 – Треугольник с определяющими параметрами
Соответствующие признаки подобия треугольников и многоугольников могут быть переформулированы в терминах критериев подобия. Подчеркнем, что при геометрическом подобии, длины элементов объектов, связанные с натурой, могут быть получены простым пересчетом соответствующих величин, относящихся к модели.
О физическом подобии Теперь введем понятие физически подобных объектов (систем, процессов и т.п.), как обобщение подобия геометрического. Два объекта называются физически подобными, если при заданных характеристиках одного можно получить соответствующие характеристики другого простым пересчетом, аналогичным пересчету при геометрическом подобии. Физическая задача. На прямоугольном кронштейне (рисунок 10.5) висит тело, масса m которого 5,5 кг. Угол между укосиной и стенкой α = 35º. Определите силы упругости, возникающие в поперечине АВ и укосине ВС.
Сначала найдем вертикальную силу Р, с которой тело с массой m действует в точке В: Р = 5,5 кг · 9,81 м/с2 = 54 Н. Теперь разложим силу Р по направлениям АВ и ВС (Рисунок 5). Для этого выбираем масштаб сил: 2 Н в 1 мм длины и строим в этом масштабе силовой ∆A1B1С1 (Рисунок 10.6). С этой целью из точки A1 проведем A1B1׀׀ АВ, A1С1׀׀АС, A1С1= 27 (мм) и С1B1 под углом α = 35º к С1А1 до пересечения с лучом A1B1. Измерив длины A1B1 и С1B1, соответственно получим 19 мм и 33 мм. Значит, сила, возникающая в поперечине равна 38 Н и в укосине 66 Н Для повышения точности измерений, треугольники лучше строить в более крупном виде на отдельном листе, например А4. Подчеркнем, что экспериментальный подход не противоречит математическим расчетам, а дополняет их построениями подобных фигур и измерениями их элементов. В этой связи укажем на применение принципа подобия для измерения ускорения силы тяжести на Луне с помощью телевизора («Квант» № 4, за 1972 г., с. 18). В указанной заметке рассказывалось о том, что преподаватель американского колледжа смотрел у себя дома по телевизору высадку астронавтов на Луну. Вдруг он заметил, что из одного отсека корабля свисал, качаясь на чем-то вроде каната, какой-то тяжелый предмет. Тогда у преподавателя и возникла мысль об измерении ускорения силы тяжести на поверхности Луны с помощью телевизора. Если измерить на его экране длины отрезков, соответствующие росту астронавта Рассмотрим ещё вопрос, который обсуждают персонажи знаменитого трактата Галилея ”Беседы и математические доказательства, касающиеся двух новых отраслей науки”. Почему не бывает животных, какой угодно величины? Почему, например, нет слонов в три раза большего роста, чем существуют, но тех же пропорций? Ответ таков: стань слон в три раза больше, вес его тогда увеличился бы в 27 раз, как куб размера, а площадь сечения костей и, следовательно, их прочность только в 9 раз, как квадрат размера. Прочности костей уже не хватило бы, чтобы выдержать непомерно увеличивающийся вес. Такой слон был бы раздавлен собственной тяжестью. Рассуждение вполне строгое и убедительное. Эту строгость и убедительность ему придало знание двух функциональных зависимостей. Первая устанавливает соответствие между размерами подобных тел и их объемами: Объем изменяется как куб размера. Вторая связывает размеры подобных фигур и их площади: площадь изменяется как квадрат размера (Пухначев Ю.В., Попов Ю.П. Учись применять математику. Выпуск 1, М.: Знание 1977. – С. 16) Подтвердим важность метода подобия фактом из истории. (Григорьев Л.Г. Моделирование и технические науки. «Знание», 1967, с 32). Так, в 1870 году, английское Адмиралтейство спустило на воду броненосец «Кэптен». Известный английский ученый-кораблестроитель В. Рид, увидев этот броненосец, изготовил его модель и, на основе теории подобия установил, что он опрокинется даже при небольшом волнении моря. Но ученому, проделывающему какие-то несерьезные опыты с «игрушкой», лорды из Адмиралтейства не поверили. Броненосец вышел в море и перевернулся. Из 560 человек спаслись только 17. Погибли люди, погиб корабль. Теперь определим период колебания математического маятника (рисунок 9.1). Период Т будет однозначно определен, если задать g, l,
где Для малых колебаний справедлива формула T=с1 где с1 – постоянная, которую найдем из опыта. Возьмем маятник длиной l=1 (м) и экспериментально определим его период. С помощью секундомера находим, что этот маятник за 10 с совершает 5 колебаний. Поэтому Т=2 c. Таким образом 2=c1 т.е. c1=6,27, тогда как теоретически При малых При исследовании подобных явлений большое значение имеет так называемая Вид зависимости (10.3) непосредственно следует из равенства (9.8), если в последнем обе части разделить на Использование Так, длина окружности l определяется eе радиусом
Математический анализ не менее всеобъемлющ, чем сама природа: он определяет все ощутимые взаимосвязи, измеряет времена, пространства, силы, температуры… Ж. Фурье
Поиск по сайту: |
 .
.
 .
.

 безразмерная величина (число) – критерий подобия. Из двух величин «а» и «b», очевидно, можно составить только один независимый безразмерный комплекс (все другие могут через него выражаться, зависеть от него)
безразмерная величина (число) – критерий подобия. Из двух величин «а» и «b», очевидно, можно составить только один независимый безразмерный комплекс (все другие могут через него выражаться, зависеть от него) 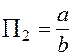 . Теперь нетрудно установить, что если у двух треугольников критерии
. Теперь нетрудно установить, что если у двух треугольников критерии  и
и  – одинаковы, то они подобны. Действительно: пусть второй треугольник однозначно определяется параметрами Φ, А, В, тогда при
– одинаковы, то они подобны. Действительно: пусть второй треугольник однозначно определяется параметрами Φ, А, В, тогда при 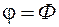 ,
,  , т.е.
, т.е. 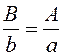 , и следовательно, треугольники подобны.
, и следовательно, треугольники подобны.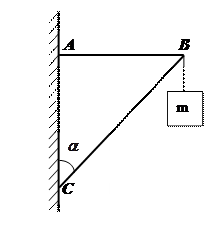 Рисунок 10.5
Рисунок 10.5
 Рисунок 10.6
Рисунок 10.6
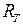 и подвесу маятника
и подвесу маятника 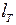 в вертикальном положении, то зная истинный рост астронавта R и обозначив истинную длину подвеса через
в вертикальном положении, то зная истинный рост астронавта R и обозначив истинную длину подвеса через 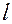 можнона основании подобия записать пропорцию
можнона основании подобия записать пропорцию  , откуда
, откуда  . Подставив в последнюю формулу известные значения величин, находящихся в её правой части, был найден результат:
. Подставив в последнюю формулу известные значения величин, находящихся в её правой части, был найден результат:  (см). Период колебаний, за которыми следил преподаватель, он определил по секундной стрелке часов: 5 с. Отсюда, пользуясь формулой для периода колебаний маятника
(см). Период колебаний, за которыми следил преподаватель, он определил по секундной стрелке часов: 5 с. Отсюда, пользуясь формулой для периода колебаний маятника 
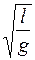 , можно оценить и ускорение силы тяжести на поверхности Луны: g
, можно оценить и ускорение силы тяжести на поверхности Луны: g 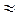 160 см/с2. Эта величина составляет
160 см/с2. Эта величина составляет  ускорения силы тяжести на поверхности Земли. Так, не выходя из дому, с помощью телевизора и метода подобия был произведён настоящий «космический» эксперимент.
ускорения силы тяжести на поверхности Земли. Так, не выходя из дому, с помощью телевизора и метода подобия был произведён настоящий «космический» эксперимент.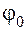 и начальные условия при t=0, φ=φ0 и
и начальные условия при t=0, φ=φ0 и  . Таким образом, период колебаний маятника является функцией Т = F(g,l,φ0) (силами сопротивления пренебрегаем). Простые преобразования, приведенные в пункте 9.3, показывают, что
. Таким образом, период колебаний маятника является функцией Т = F(g,l,φ0) (силами сопротивления пренебрегаем). Простые преобразования, приведенные в пункте 9.3, показывают, что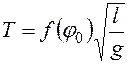 , (10.2)
, (10.2) - единственный определяющий критерий подобия, так как только этим критерием определяется выражение f(
- единственный определяющий критерий подобия, так как только этим критерием определяется выражение f(  )
)  , т.е. период колебаний. В формуле (10.2) критерий
, т.е. период колебаний. В формуле (10.2) критерий 
 при
при  для модели и натуры, то колебания маятников подобны. Проверим это утверждение и непосредственно. Пусть lм, Тм – длина и период маятника модели, а lн ,Тн – для натуры, тогда на основании (10.2) имеем
для модели и натуры, то колебания маятников подобны. Проверим это утверждение и непосредственно. Пусть lм, Тм – длина и период маятника модели, а lн ,Тн – для натуры, тогда на основании (10.2) имеем  и
и 
 . Откуда
. Откуда  и
и  , или
, или  , где коэффициент подобия
, где коэффициент подобия  , т. е. если мы найдем на основе эксперимента Тм для модели и измерим lм и lн , то легко получим Тн для натуры. Итак,
, т. е. если мы найдем на основе эксперимента Тм для модели и измерим lм и lн , то легко получим Тн для натуры. Итак,  , т. е. при заданном периоде Тм одного маятника получаем соответствующий период Тн другого простым пересчетом, аналогичным пересчету при геометрическом подобии.
, т. е. при заданном периоде Тм одного маятника получаем соответствующий период Тн другого простым пересчетом, аналогичным пересчету при геометрическом подобии. ,
, ,
, =2
=2  . Отсюда Т
. Отсюда Т  6,27
6,27  и lм=1м мы нашли на основе опыта Тм=2 с. Пусть lн=0,49 м тогда
и lм=1м мы нашли на основе опыта Тм=2 с. Пусть lн=0,49 м тогда 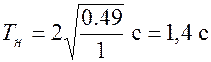 . Сравним этот результат с экспериментальным, взяв маятник длины 0,49 м, тогда обнаружим, что он совершает 10 колебаний за 14 с, т.е. Т =1,4 с. Таким образом, пересчет соответствует эксперименту.
. Сравним этот результат с экспериментальным, взяв маятник длины 0,49 м, тогда обнаружим, что он совершает 10 колебаний за 14 с, т.е. Т =1,4 с. Таким образом, пересчет соответствует эксперименту. (пи) - теорема. Функциональная зависимость между характеризующими объект или процесс величинами может быть представлена в виде зависимости между составленными из них критериями подобия:
(пи) - теорема. Функциональная зависимость между характеризующими объект или процесс величинами может быть представлена в виде зависимости между составленными из них критериями подобия: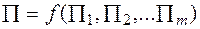 . (10.3)
. (10.3) и ввести для критерия
и ввести для критерия  .
.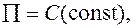 т.е. в этом случае анализ размерностей позволяет получить полное решение задачи с точностью до постоянной, которая может быть найдена из эксперимента.
т.е. в этом случае анализ размерностей позволяет получить полное решение задачи с точностью до постоянной, которая может быть найдена из эксперимента. , и из двух этих величин можно образовать только один безразмерный комплекс
, и из двух этих величин можно образовать только один безразмерный комплекс 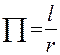 , поэтому функциональная зависимость имеет вид
, поэтому функциональная зависимость имеет вид  ; c, как показано выше, легко может быть определена экспериментально и
; c, как показано выше, легко может быть определена экспериментально и  ( точно 2
( точно 2 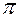 ).
).