 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
О геометрическом подобии
По-видимому, на практике исторически первым применялось математическое моделирование, основанное на принципе подобия алгебраически описываемом пропорцией, представляющей равенство двух отношений или с функциональной точки зрения – функцией Две геометрические фигуры подобны, если отношения длин всех соответственных элементов одинаковы. Например, картина и ее фотоснимок представляют подобные фигуры. Если известен коэффициент подобия – масштаб, то простым умножением на величину масштаба линейных размеров – длин отрезков или дуг – одной геометрической фигуры получают соответствующие размеры другой, ей подобной. Подчеркнем, что на возникающий при этом вопрос, каким по величине мы увидим, например угол в 9 градусов, если будем рассматривать его в лупу с десятикратным увеличением, ответ однозначный: таким же, он не изменится. Пусть, например, требуется определить высоту треугольной в плане башни, не производя непосредственно измерение высоты (рисунок 10.1). Если имеется фотоснимок башни, то, используя условие подобия можно довольно просто получить результат.
Рисунок 10.1 – Подобие объектов
Измерив, легкодоступный размер
Рисунок 10.2 – подобие кругов
Поскольку все окружности (круги) подобны, то, рассмотрев рисунок 10.2, можно написать равенство
Установим также формулу площади круга. Так как все круги подобны, то из того же рисунка на основании теоремы о том, что площади подобных фигур относятся как квадраты сходственных отрезков, следует:
Учитывая, что все круги подобны, приходим к выводу, что Поскольку объемы пространственных подобных фигур относятся как кубы сходственных отрезков, то для двух шаров, большие круги которых указаны на рисунке 10.2, имеем:
Поэтому Отметим, что площади сферических поверхностей относятся как квадраты их радиусов и потому В случае геометрического подобия изучение натуры при помощи ее модели довольно простое: отношение длин сходственных отрезков постоянно, площади подобных фигур пропорциональны квадратам длин их сходственных линий, объемы подобных тел, а также объемы любых соответственных их частей пропорциональны кубам длин их сходственных линий. Однако, если очевидны утверждения: любые две окружности подобны, любые два равносторонних треугольника подобны, картина и ее соответствующий фотоснимок подобны, то в более сложных ситуациях нужно знать достаточные условия подобия, чтобы из них можно было делать соответствующие выводы.
Поиск по сайту: |
 . Для получения необходимых экспериментальных данных с целью определения величин, входящих в пропорцию или коэффициента
. Для получения необходимых экспериментальных данных с целью определения величин, входящих в пропорцию или коэффициента 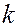 в линейную функцию используются удобные для исследования масштабы. Различают подобие геометрическое и физическое.
в линейную функцию используются удобные для исследования масштабы. Различают подобие геометрическое и физическое.
 на натуре и размеры
на натуре и размеры  и
и 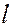 на модели (фотоснимке) на основании подобия, составим пропорцию
на модели (фотоснимке) на основании подобия, составим пропорцию  и найдем:
и найдем:  . Такой подход всегда применим, если известно, что соответствующие фигуры подобны. В этой связи отметим, что точнее было бы говорить о подобии математических моделей объектов, так как сами объекты могут обладать и некоторыми особенностями, не включенными в модель.
. Такой подход всегда применим, если известно, что соответствующие фигуры подобны. В этой связи отметим, что точнее было бы говорить о подобии математических моделей объектов, так как сами объекты могут обладать и некоторыми особенностями, не включенными в модель.
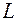 – длина окружности радиуса
– длина окружности радиуса  ,
, – длина окружности радиуса
– длина окружности радиуса 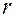
 или
или 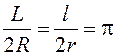 (
(  ) и, следовательно,
) и, следовательно,  . Постоянное число
. Постоянное число 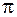 можно определить из эксперимента с любым круговым диском (моделью). Так, взяв и измерив длины его диаметра и граничной окружности, легко оценим
можно определить из эксперимента с любым круговым диском (моделью). Так, взяв и измерив длины его диаметра и граничной окружности, легко оценим  или
или  , где
, где  – константа. Поэтому
– константа. Поэтому  .
. – величина постоянная:
– величина постоянная:  и может быть приближенно определена экспериментально, например, взвешиваниями круга и единичного квадрата, вырезанных из однородного тонкого картона. При этом получается:
и может быть приближенно определена экспериментально, например, взвешиваниями круга и единичного квадрата, вырезанных из однородного тонкого картона. При этом получается: 
 . Итак,
. Итак,  .
. или
или 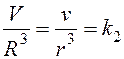 , где
, где  – константа.
– константа. , т.е.
, т.е.  и
и  , точно
, точно 
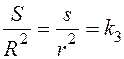 , где
, где  –константа. Следовательно,
–константа. Следовательно,  , причем
, причем