 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Разнородные величины нельзя суммировать
друг с другом, имеет важнейшее значение для теории размерностей. Г. Хантли В физике…нет места для путаных мыслей… Действительно понимающие природу того или иного явления должны получать основные законы из соображений размерности. Э. Ферми. МЕТОД РАЗМЕРНОСТЕЙ С ПРИЛОЖЕНИЯМИ К ПОСТРОЕНИЮ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ Размерные и безразмерные величины Величины, числовые значения которых зависят от единиц измерения называются именованными или, по-научному, размерными. Так можно записать, что длина одного и того же отрезка равна 10 м = 100 дм =1000 см = 0,01 км. Величины, числовые значения которых не зависят от единиц измерения, называются неименованными, безразмерными или отвлеченными. Классическим примером безразмерной величины является число π = l/d, где l – длина окружности, d её диаметр, с тремя значащими цифрами π ≈ 3.14. Несмотря на отвлеченный характер этого числа, оно имеет широкие применения. С его помощью вычисляют не только длину окружности (l = πd), но и площадь круга, боковую и полную поверхность прямого кругового цилиндра, конуса, площадь сферы, объемы соответствующих пространственных фигур. Через π, выражается период малых колебаний математического маятника и многих других физических величин. Оно наверняка встретится в будущем при формулировках новых законов и закономерностей объективной действительности. Вот эти обстоятельства объясняют его популярность. А физик из Сан Франциско обратил внимание на то, что в американском формате запись даты 3.14 – означает: 14 марта. Он предложил 14 марта объявить всемирным, международным праздником «День числа π», который впервые был отмечен в научно-популярном музее Сан Франциско в 1988 г. Характерной особенностью безразмерных величин является возможность производить с ними все математические операции. В противоположность им величины разных размерностей нельзя складывать и сравнивать. Не имеют смысла сравнения: что больше 8 км или 5 кг, равны ли величины 5 км и 5 минут, или чему равна сумма 8 км + 5 кг, но можно складывать величины одной размерности: 7 км + 2 км = 9 км. Такие величины можно сравнивать: 7 км >3 км. Эти особенности размерных величин следует иметь в виду особенно при составлении формул, содержащих именованные величины.
О структуре функциональной связи Многие закономерности, устанавливаемые наукой, представляют собой функциональные зависимости между размерными (именованными) величинами, характеризующими процессы, явления или объекты, понимаемые в самом широком смысле. Это обстоятельство накладывает соответствующие ограничения на структуру функциональной связи
Простейшие задачи
Сначала установим формулу зависимости объема шара от радиуса. Поскольку шар полностью определяется величиной радиуса, Конечно, в этой задаче структура функциональной связи была очевидной. Теперь рассмотрим более сложный пример определения структуры функциональной зависимости пути, пройденного при падении материальной точки (при отсутствии сопротивления и при начальной скорости
На основании сказанного выше, можно написать, что
где Отсюда Из выражения (9.2) имеем: Поскольку из параметров Отметим, что в свое время оппоненты Галилея утверждали, что Тогда где . Значит
т.е. В качестве ещё одного примера определим период колебания математического маятника (рисунок 9.1).
Рисунок 9.1 – Модель математического маятника
Период его колебаний Вообще, для установления структуры функциональной связи удобно входящие в нее величины свести в таблицу, которая в рассматриваемом случае примет вид:
Как и выше, представим
Следовательно, имеет место система:
из которой и степенная комбинация
где
где постоянная с1 может быть найдена, например, из опыта.
Поиск по сайту: |
 : размерности левой и правой части равенства должны быть одинаковы. Именно этот факт во многих случаях позволяет устанавливать вид функциональной зависимости между величинами на основании анализа размерностей, с учетом того, что произведение величин с основаниями даже разных размерностей и рациональными показателями степеней может иметь физический смысл, тогда как сумма или разность величин неодинаковых размерностей смысла не имеет.
: размерности левой и правой части равенства должны быть одинаковы. Именно этот факт во многих случаях позволяет устанавливать вид функциональной зависимости между величинами на основании анализа размерностей, с учетом того, что произведение величин с основаниями даже разных размерностей и рациональными показателями степеней может иметь физический смысл, тогда как сумма или разность величин неодинаковых размерностей смысла не имеет.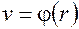 и
и  измеряется в м, а
измеряется в м, а  – в м3, то задача сводится к отысканию такой математической операции, которая «превращает» метры погонные в метры кубические. Очевидно, существует только одна такая операция. Это – возведение в куб. Поэтому
– в м3, то задача сводится к отысканию такой математической операции, которая «превращает» метры погонные в метры кубические. Очевидно, существует только одна такая операция. Это – возведение в куб. Поэтому  , где
, где  – безразмерная постоянная, так как шар однозначно определяется величиной радиуса, имеющего размерность длины. Число с можно определить экспериментально, полностью погрузив однородный шарик, например от подшипника, в мерный сосуд с водой:
– безразмерная постоянная, так как шар однозначно определяется величиной радиуса, имеющего размерность длины. Число с можно определить экспериментально, полностью погрузив однородный шарик, например от подшипника, в мерный сосуд с водой:  , точно
, точно 
 .
. ), от ускорения свободного падения
), от ускорения свободного падения 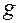 и времени
и времени 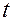 , т.е.
, т.е.
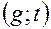 . (9.1)
. (9.1) , (9.2)
, (9.2) – безразмерная величина, a и b – рациональные числа. Тогда, записав уравнение размерности, соответствующее общей формуле (9.2), получим:
– безразмерная величина, a и b – рациональные числа. Тогда, записав уравнение размерности, соответствующее общей формуле (9.2), получим: 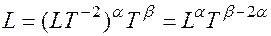 .
. т.е.
т.е.  .
. (9.3).
(9.3). и
и  , определяющих величину
, определяющих величину 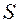 в (9.3) можно составить только одну комбинацию
в (9.3) можно составить только одну комбинацию 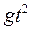 (a и b в (9.2) определены однозначно), имеющую размерность
(a и b в (9.2) определены однозначно), имеющую размерность  , т.е.
, т.е.  и
и  , тогда
, тогда 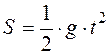 .
. зависит от массы тела
зависит от массы тела  . Галилей экспериментально показал, что одновременно сброшенные с Пизанской башни (с начальной скоростью равной нулю) два камня – тяжелый и легкий – падают на землю также одновременно. Однако опыт не убедил оппонентов. Посмотрим, какой ответ на этот вопрос дает нам анализ структуры соответствующей функциональной связи. Итак, пусть
. Галилей экспериментально показал, что одновременно сброшенные с Пизанской башни (с начальной скоростью равной нулю) два камня – тяжелый и легкий – падают на землю также одновременно. Однако опыт не убедил оппонентов. Посмотрим, какой ответ на этот вопрос дает нам анализ структуры соответствующей функциональной связи. Итак, пусть 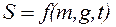 (9.4)
(9.4) , (9.5)
, (9.5) – безразмерная величина, d, a и b – рациональные числа. Теперь, записав уравнение размерности, соответствующее общей формуле (9.5), получим:
– безразмерная величина, d, a и b – рациональные числа. Теперь, записав уравнение размерности, соответствующее общей формуле (9.5), получим:  .
.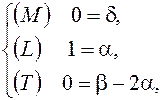
 . Отсюда следует, что правая часть (9.4) и вместе с ней и левая не зависят от массы, что подтверждает правоту Галилея.
. Отсюда следует, что правая часть (9.4) и вместе с ней и левая не зависят от массы, что подтверждает правоту Галилея.
 будет однозначно определен, если задать
будет однозначно определен, если задать  и начальные условия: при
и начальные условия: при  и
и  . Таким образом, период колебаний маятника является функцией
. Таким образом, период колебаний маятника является функцией  (силами сопротивления пренебрегаем).
(силами сопротивления пренебрегаем).
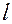




 , где
, где 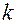 и
и  – безразмерные величины, а
– безразмерные величины, а  .
.
 ,
, , то
, то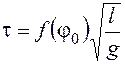 , (9.6)
, (9.6) функция только одного безразмерного аргумента
функция только одного безразмерного аргумента  и структура зависимости (9.6) соответствует основной теореме. Из соображений симметрии, очевидно, что
и структура зависимости (9.6) соответствует основной теореме. Из соображений симметрии, очевидно, что  имеем
имеем  т.е. для малых колебаний члены со степенями
т.е. для малых колебаний члены со степенями  и выше отбрасываем, тогда для периода получим формулу
и выше отбрасываем, тогда для периода получим формулу , (9.7)
, (9.7)