 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Побудова еліпса по точках⇐ ПредыдущаяСтр 19 из 19
Оскільки точка
Провівши через точку
Параметричні рівняння еліпса
Нехай даний еліпс задається канонічним рівнянням
Розглянемо коло
яке переходить у даний еліпс в результаті стиску
Нехай Тоді і, отже,
Рівняння
і є параметричними рівняннями еліпса. Параметр
Гіпербола
Гіперболою – називається геометричне місце точок, різниця відстаней яких до 2-х даних точок, називаних фокусами, є величина стала (ця стала величина повинна бути додатною і менше відстані між фокусами) (рис. 3.17).
Позначимо цю сталу через За означенням гіперболи:
Оскільки
то або
Піднісши обидві частини останньої рівності до квадрату, одержимо
відкіля
Підведемо ще раз це рівняння до квадрату
Оскільки різниця 2-х сторін трикутника менше 3-ї його сторони, то Покладемо
Тоді одержимо
і остаточно
Відзначимо властивості лінії, визначеної рівнянням (11). Ця лінія симетрична щодо осей координат і відносно початку координат. Оскільки Число Відзначимо ще одну особливість форми досліджуваної лінії. Розглянемо разом з гіперболою дві прямі: Дійсно, Разом з тим, оскільки
то різниця Прямі
до яких як завгодно близько при Якщо уявна вісь гіперболи направлена по осі
Ексцентриситетом гіперболи називається відношення відстані між фокусами до її дійсної осі:
Для гіперболи, що обчислюється за формулою (13) ексцентриситет обчислюється так:
Асимптоти гіперболи (13) обчислюються так само, як і в гіперболи (11) за формулами (12). Гіперболи (11) і (13) називаються спряженими. Гіпербола називається рівносторонньою, якщо її дійсна і уявна осі рівні, тобто
Асимптоти гіпербол (15) і (16) взаємно перпендикулярні.
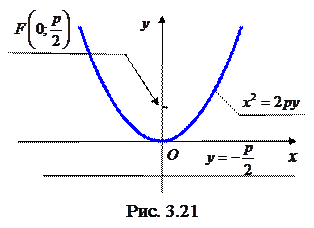
Парабола Параболою називається множина точок, рівновіддалених від даної точки, що називається фокусом і даної прямої, яка називається директрисою (рис.3.19).
За означенням
Тоді формула параболи в обраній системі координат буде:
(18) – канонічне рівняння параболи.
У залежності від розташування параболи відносно системи координат запишемо її рівняння (рис.3.20, 3.21, 3.22).
Задачі 1. Відстань між фокусами еліпса дорівнює
Розв’язання.
2. Знайти дотичні до еліпса Відповідь:
3. Дано гіперболу Відповідь:
4. Знайти довжини осей, координати фокусів і ексцентриситет гіперболи, заданої рівнянням: а) б) Відповідь: а) Дійсна вісь гіперболи дорівнює
б) Дійсна вісь гіперболи дорівнює
Питання для самоконтролю: 16. Поняття про рівняння лінії. Загальне рівняння прямої лінії на площині і його дослідження. 17. Рівняння прямої лінії на площині з кутовим коефіцієнтом. Рівняння прямої, що проходить через дану точку в заданому напрямку. 18. Рівняння прямої, що проходить через дві задані точки. Рівняння прямої у відрізках. 19. Кут між двома прямими. Умови паралельності і перпендикулярності двох прямих. Відстань від точки до прямої. 20. Загальне рівняння площини та його дослідження. 21. Рівняння площини, що проходить через одну і три точки. 22. Кут між площинами. Умови паралельності і перпендикулярності двох площин. 23. Параметричні рівняння прямої лінії в просторі. Канонічне рівняння прямої лінії в просторі, що проходить через дві дані точки. 24. Кут між двома прямими в просторі. Умова паралельності і перпендикулярності двох прямих в просторі. 25. Точка перетину прямої і площини. Кут між прямою та площиною. Умови паралельності та перпендикулярності прямої та площини. 26. Криві другого порядку – коло, еліпс. Півосі, фокуси, ексцентриситет еліпсу. 27. Гіпербола, її канонічне рівняння, півосі, фокуси, ексцентриситет, асимптоти. 28. Парабола, її канонічне рівняння, фокус і директриса параболи.
Тести до розділу 3 11. Вказати рівняння прямої, що проходить через дві точки: а) 12. Вказати рівняння прямої у відрізках: а) 13. Знайти координати точки 14. Які з даних прямих перпендикулярні до прямої а) 15. Знайти відстань між паралельними прямими 16. Знайти координати центра 17. Знайти відстань 18. Знайти відповідність між твердженнями відносно двох площин
прямою 1) площини паралельні а) 2) площини перпендикулярні б) 3) площина (1) і пряма паралельні в) 4) площина (1) і пряма перпендикулярні г) 19. Скласти рівняння площини, що проходить через точку Відповідь: 20. Через точку Відповідь:
Відповіді: 1.
Поиск по сайту: |
 Побудуємо два кола з центром на початку координат і радіусами
Побудуємо два кола з центром на початку координат і радіусами 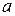 і
і 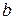 , рівними відповідно великій і малій півосям еліпса. Проведемо з початку координат промінь під кутом
, рівними відповідно великій і малій півосям еліпса. Проведемо з початку координат промінь під кутом  до осі абсцис
до осі абсцис  (рис. 3.15). Нехай
(рис. 3.15). Нехай 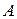 й
й 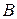 точки його перетину з побудованими колами.
точки його перетину з побудованими колами. 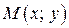 – точка перетину прямих, проведених з
– точка перетину прямих, проведених з  . Точка
. Точка 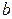 , для якого осі координат є осями симетрії. Тоді, координати точки
, для якого осі координат є осями симетрії. Тоді, координати точки 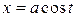 ,
, 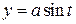 .
.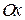 , то точки
, то точки 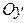 , то точки
, то точки 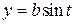 . Отже, точка
. Отже, точка 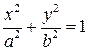 .
.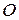 різні промені, ми зазначеним шляхом побудуємо скільки завгодно точок еліпса.
різні промені, ми зазначеним шляхом побудуємо скільки завгодно точок еліпса. У багатьох задачах буває корисним використання параметричних рівнянь еліпса.
У багатьох задачах буває корисним використання параметричних рівнянь еліпса.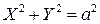 , (7)
, (7)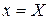 ,
,  . (8)
. (8)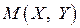 – довільна точка даного еліпса (рис. 3.16),
– довільна точка даного еліпса (рис. 3.16), 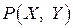 – її прообраз на колі (7). Позначимо через
– її прообраз на колі (7). Позначимо через  кут від додатного напрямку осі
кут від додатного напрямку осі 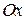 до променя
до променя 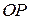 .
.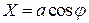 ,
, 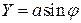
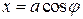 ,
,  .
.
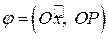 .
.
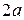 , відстань між фокусами –
, відстань між фокусами –  . Нехай
. Нехай 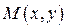 – довільна точка гіперболи.
– довільна точка гіперболи.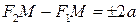 . (9)
. (9)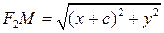
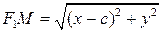 ,
,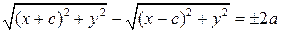 ,
,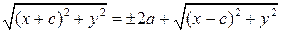 .
.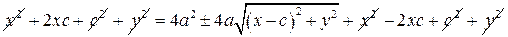 ,
, .
.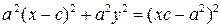 ;
;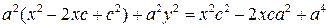 ;
; ;
; .
. .
.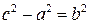 . (10)
. (10)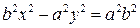 ,
,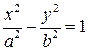 . (11)
. (11)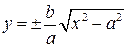 , то для всіх точок кривої справедливо
, то для всіх точок кривої справедливо  , і немає точок кривої в смузі
, і немає точок кривої в смузі  . Крива складається, отже, з 2-х окремих частин – гілок гіперболи, одна з яких лежить в області
. Крива складається, отже, з 2-х окремих частин – гілок гіперболи, одна з яких лежить в області  (права і ліва гілки гіперболи).
(права і ліва гілки гіперболи). і
і  – її фокусами.
– її фокусами.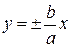 . Легко бачити, що в 1-й чверті (унаслідок симетрії лінії досить розглядати 1-у чверть) при одній і тій же абсцисі ординати точок гіперболи менше ординат відповідних точок прямої
. Легко бачити, що в 1-й чверті (унаслідок симетрії лінії досить розглядати 1-у чверть) при одній і тій же абсцисі ординати точок гіперболи менше ординат відповідних точок прямої 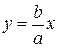 .
.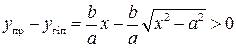 .
.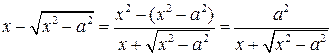 ,
,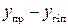 прагне до нуля при необмеженому зростанні
прагне до нуля при необмеженому зростанні 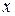 , і тому точки гіперболи при необмеженому збільшенні абсцис, як завгодно близько підходять до відповідних точок прямої
, і тому точки гіперболи при необмеженому збільшенні абсцис, як завгодно близько підходять до відповідних точок прямої 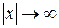 підходять точки гілок гіперболи, називаються асимптотами гіперболи. Легко бачити, що асимптоти гіперболи направлені по діагоналях прямокутника зі сторонами
підходять точки гілок гіперболи, називаються асимптотами гіперболи. Легко бачити, що асимптоти гіперболи направлені по діагоналях прямокутника зі сторонами 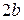 , симетрично щодо осей симетрії гіперболи.
, симетрично щодо осей симетрії гіперболи.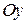 , то рівняння гіперболи має вигляд (рис. 3.18):
, то рівняння гіперболи має вигляд (рис. 3.18):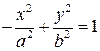 . (13)
. (13)
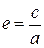 . (14)
. (14)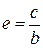 . (14')
. (14')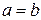 . Найпростіше рівняння рівносторонньої гіперболи має вигляд:
. Найпростіше рівняння рівносторонньої гіперболи має вигляд: . (15)
. (15)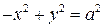 . (16)
. (16) Величина
Величина 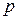 , рівна відстані від фокуса до директриси, називається параметром параболи; пряма що проходить через фокус параболи перпендикулярно її директрисі, називається віссю, а точка перетину параболи з її віссю – вершиною параболи.
, рівна відстані від фокуса до директриси, називається параметром параболи; пряма що проходить через фокус параболи перпендикулярно її директрисі, називається віссю, а точка перетину параболи з її віссю – вершиною параболи. . (17)
. (17)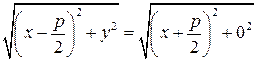 ;
;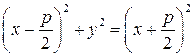 ;
; ;
;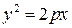 . (18)
. (18)

 , відстань між його директрисами дорівнює
, відстань між його директрисами дорівнює 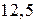 (рис.3.23). Знайти найпростіше рівняння цього еліпса.
(рис.3.23). Знайти найпростіше рівняння цього еліпса.
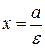 – директриси;
– директриси;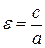 ;
;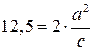 ;
;  .
. ;
;  ;
;  ;
; 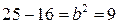 .
.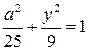 .
.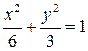 , перпендикулярні до прямої
, перпендикулярні до прямої  .
.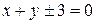 .
. . Написати рівняння асимптот.
. Написати рівняння асимптот.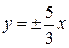 .
.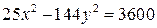 ;
;
 .
.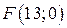 ,
, 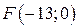 ,
, 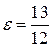 .
.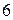 , уявна
, уявна 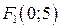 ,
, 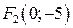 ,
, 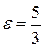 .
.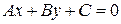 ; б)
; б) 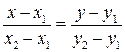 ; в)
; в) 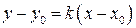 .
.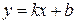 ; б)
; б)  .
. перетину медіан трикутника
перетину медіан трикутника  , де
, де 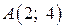 ,
,  ,
,  .
. :
: ; б)
; б) 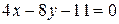 ; в)
; в) 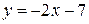 ; г)
; г) 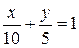 ; д)
; д) 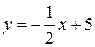 .
. і
і 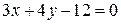 .
.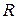 кола
кола  .
.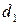 між фокусами еліпса
між фокусами еліпса 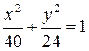 і
і 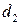 між фокусами гіперболи
між фокусами гіперболи  .
.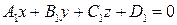 , (1)
, (1)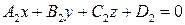 , (2)
, (2)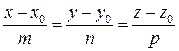 і їх ознаками:
і їх ознаками: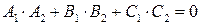 ;
;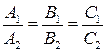 ;
;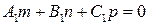 ;
;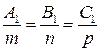 .
.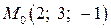 паралельно площині
паралельно площині 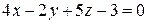 .
.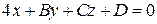 , де
, де  …,
…, 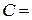 …,
…,  ….
….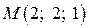 провести площину, перпендикулярну до прямої
провести площину, перпендикулярну до прямої 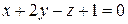 ,
,  .
. , де
, де  . 2.
. 2. 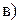 . 3.
. 3. 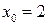 ,
, 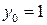 . 4.
. 4.  ;
;  ;
;  . 5.
. 5. 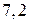 . 6.
. 6.  ,
, 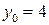 ;
; 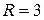 . 7.
. 7. 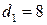 ;
; 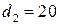 . 8.
. 8.  –
– 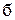 ;
;  –
– 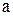 ;
; 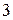 –
– 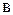 ;
; 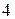 –
– 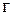 . 9.
. 9. 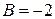 ;
;  ;
; 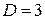 . 10.
. 10. 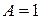 ;
; 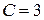 ;
;  .
.