 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Лінійні дії з векторами, заданими розкладом в ортонормованому базисі. Умови колінеарності векторів
Нехай задані два вектора своїм розкладом в ортонормованому базисі
а) При складанні векторів однойменні проекції їх складуються
б) Щоб відняти два вектори, треба відняти їх проекції
в) Щоб помножити вектор на число треба помножити його проекції на число
Умова колінеарності двох векторів є пропорційність їх координат:
Ділення відрізку в даному співвідношенні
Задача № 1.Знайти координати точки Розв’язання. Нехай задані дві точки Знайдемо координати точки
Із цього прямує, що і модулі векторів
Для координат
Поклавши
тобто, координати середини відрізка дорівнюють полусумі координат його початку і кінця.
Скалярний добуток векторів, його означення, фізичний зміст, властивості Задача № 2.Треба знайти роботу сили Якщо точка пересувається по напрямку сили, то по означенню, робота сили дорівнює добутку величини сили на довжину переміщення, тобто Якщо ж точка пересувається під кутом
Отже, робота сили дорівнює:
Скалярним добутком двох векторів називається число рівне добутку їх довжин, помноженому на косинус кута між ними
або
Скалярний добуток двох векторів дорівнює довжині одного з них помноженого на проекцію другого вектора по напрямку першого.
Основні властивості скалярного добутку В векторному численні величину Алгебраїчні властивості скалярного добутку 1о. Скалярний добуток обертається в нуль в тому і тільки в тому випадку, коли, по крайній мірі, один із векторів є нульовим, або якщо вектори перпендикулярні. Доведення. Скалярний добуток дорівнює нулю, якщо 2о. Скалярний добуток має властивість комутативності 3о. До скалярного добутку можна застосувати дистрибутивний закон. Щоб помножити суму векторів треба помножити кожний доданок, і скласти отримані добутки
4о. Асоціативна властивість відносно множення на число
Поиск по сайту: |
 ;
;  .
. ;
; ;
;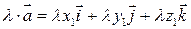 .
. .
. , яка ділить даний відрізок
, яка ділить даний відрізок  в заданому співвідношенні (рис.2.6).
в заданому співвідношенні (рис.2.6).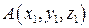 і
і  , й дано співвідношення
, й дано співвідношення  , в якому деяка точка
, в якому деяка точка 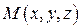 ділить спрямований відрізок
ділить спрямований відрізок  .
.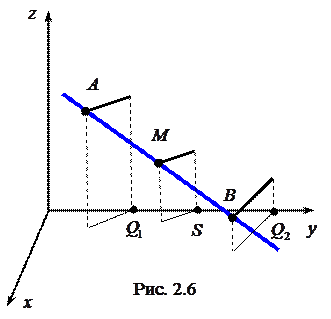 Нехай
Нехай  ,
, 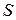 ,
,  – проекції точок
– проекції точок 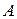 ,
, 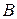 на вісь
на вісь 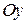 . Тоді
. Тоді 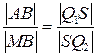 , тобто відрізки двох прямих, укладених між паралельними площинами, пропорційні.
, тобто відрізки двох прямих, укладених між паралельними площинами, пропорційні. задовольняють аналогічному співвідношенню:
задовольняють аналогічному співвідношенню:  . Оскільки
. Оскільки  ;
;  , а за умовою
, а за умовою  , то рівняння матиме вигляд
, то рівняння матиме вигляд ;
; ;
;  ;
;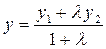 .
.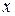 і
і  будемо мати:
будемо мати: ;
; 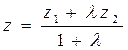 .
. , знайдемо координати середини відрізка
, знайдемо координати середини відрізка ;
; 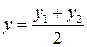 ;
; 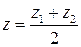 ,
, , якщо точка, на яку діє сила, здійснила переміщення
, якщо точка, на яку діє сила, здійснила переміщення  рівне
рівне  .
. .
. до напрямку сили, то працює тільки той доданок сили
до напрямку сили, то працює тільки той доданок сили  , що має напрям по лінії
, що має напрям по лінії  , а перпендикулярний доданок урівноважиться опором (рис. 2.7).
, а перпендикулярний доданок урівноважиться опором (рис. 2.7). .
. .
.
 ,
, ;
;  .
.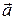 та
та  тому, що, по-перше, ця величина є скаляр і, по-друге, має деякі алгебраїчні властивості звичайного добутку чисел.
тому, що, по-перше, ця величина є скаляр і, по-друге, має деякі алгебраїчні властивості звичайного добутку чисел.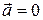 і
і  , чи навпаки
, чи навпаки  і
і  . У випадку, коли вектори-множники не є нульовими, то
. У випадку, коли вектори-множники не є нульовими, то 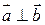 , тому що за умовою
, тому що за умовою  і при
і при  ,
, 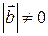 маємо
маємо  , тобто
, тобто  . Це випливає із означення.
. Це випливає із означення. .
. .
.