 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Однорідні системи лінійних рівнянь. Теорема про
Наявність ненульового розв’язку Однорідні системи лінійних рівнянь. Теорема про наявність ненульового розв’язку однорідної системи Лінійне рівняння виду
називається однорідним, якщо в ньому вільний член
Системи лінійних однорідних рівнянь (1) є частковим випадком розглянутих раніше лінійних систем Розглядаючи матрицю системи Для однорідних систем становить особливий інтерес питання про існування ненульових розв’язків. Позначимо ранг матриці системи (1) через Таким чином, має місце наступна основна теорема про однорідні системи. Теорема. Система лінійних однорідних рівнянь має ненульовий розв’язок тоді і тільки тоді, коли ранг її матриці коефіцієнтів при змінних менше числа змінних, тобто при Позначимо розв’язок системи (1)
Розв’язки системи лінійних однорідних рівнянь мають наступні властивості: 1. Якщо рядок 2. Якщо рядки Переконатися в справедливості зазначених властивостей розв’язків системи лінійних однорідних рівнянь можна безпосередньо підстановкою їх у рівняння системи. Зі сформульованих властивостей випливає, що всяка лінійна комбінація розв’язків системи лінійних однорідних рівнянь також є розв’язком цієї системи. Тому становить інтерес знайти такі лінійно незалежні розв’язки системи (1), через які лінійно виражалися б всі інші її розв’язки.
Поиск по сайту: |

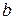 дорівнює нулю. Відповідно до цього, систему лінійних рівнянь ми назвемо однорідною, якщо всі її вільні члени дорівнюють нулю. Довільна система лінійних рівнянь має таким чином, вид
дорівнює нулю. Відповідно до цього, систему лінійних рівнянь ми назвемо однорідною, якщо всі її вільні члени дорівнюють нулю. Довільна система лінійних рівнянь має таким чином, вид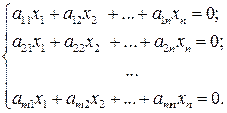 (1)
(1) .Томудля них справедлива теорема Кронекера-Капеллі.
.Томудля них справедлива теорема Кронекера-Капеллі.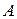 і розширену матрицю
і розширену матрицю 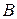 , бачимо, що матриця
, бачимо, що матриця 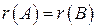 , тобто системи однорідних лінійних рівнянь завжди сумісні. Всі однорідні системи лінійних рівнянь мають по крайній мірі нульовий або тривіальний розв’язок
, тобто системи однорідних лінійних рівнянь завжди сумісні. Всі однорідні системи лінійних рівнянь мають по крайній мірі нульовий або тривіальний розв’язок  .
.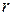 і застосуємо до неї теорему про число розв’язків. Якщо в системі
і застосуємо до неї теорему про число розв’язків. Якщо в системі  , а її визначник відмінний від нуля, то така система має тільки нульовий розв’язок, як це випливає з теореми і формул Крамера. Виходить, що ненульових розв’язків у цьому випадку немає. Ненульові розв’язки, можливі лише для таких систем однорідних лінійних рівнянь, у яких число рівнянь менше числа змінних або при їхній рівності, коли визначник системи дорівнює нулю.
, а її визначник відмінний від нуля, то така система має тільки нульовий розв’язок, як це випливає з теореми і формул Крамера. Виходить, що ненульових розв’язків у цьому випадку немає. Ненульові розв’язки, можливі лише для таких систем однорідних лінійних рівнянь, у яких число рівнянь менше числа змінних або при їхній рівності, коли визначник системи дорівнює нулю. .
. у виді рядка
у виді рядка  .
. – так само розв’язок цієї системи.
– так само розв’язок цієї системи. – розв’язки системи (1), то при будь-яких
– розв’язки системи (1), то при будь-яких  і
і  їхня лінійна комбінація
їхня лінійна комбінація  – так само розв’язок системи.
– так само розв’язок системи.