 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Точка перетину прямої і площині. Кут між прямою і площиною. Умова паралельності і перпендикулярності прямої і площини
Нехай задані рівняння прямої лінії в просторі
і рівняння площини
Для визначення координат точки перетину прямої лінії з площиною потрібно спільно розв’язати ці рівняння. Прирівнявши рівність
Підставляючи координати
Нехай
Тоді у випадку паралельності прямої
Зауваження. Ця умова отримується відразу, якщо замітимо, що вектори
Умова перпендикулярності прямої і площини співпадає з умовою паралельності цієї прямої і перпендикуляра до площини, тобто
Приклад 1. Знайти координати точки перетину прямої Відповідь:
Приклад 2. Знайти кут між прямою Відповідь:
Приклад 3. Яке повинне бути значення Відповідь:
Приклад 4. Провести через пряму Відповідь:
Приклад 5. Через точку Відповідь:
Приклад 6. Скласти рівняння площини, що проходить через точку Відповідь:
Лінії другого порядку Коло Загальне рівняння другого степеня відносно змінних Відповідно до цього загальне рівняння другого степеня можна записати у вигляді:
при цьому передбачалося, що хоча б один з коефіцієнтів Лінії, що відповідають цьому рівнянню, називаються кривими 2-го порядку. Найпростішою такою кривою є коло. Коло. Колом називається множина усіх точок площини, відстані яких від заданої точки площини (центра кола) дорівнюють сталому числу (радіусу). Круг складається з кола і внутрішніх точок. Коло з центром у точці
Це рівняння називають канонічним, рівнянням кола. Можна показати, що рівняння (2) є рівнянням другого степеня. Замітимо, що в рівнянні кола відсутній член з добутком поточних координат і коефіцієнти при квадратах поточних координат рівні між собою.
Еліпс
Виберемо систему прямокутних декартових координат так, щоб вісь абсцис проходила через обидві задані точки Нехай
За означенням еліпса
або
або
Розділивши обидві частини останнього рівняння на
Покладемо
Тоді остаточно одержимо рівняння:
Зробимо деякі зауваження про форму лінії, що відповідає отриманому рівнянню (рис.3.14). Оскільки Точки Зі зміною Якщо ж Число
Поиск по сайту: |
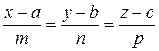 (*)
(*)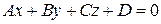 . (**)
. (**)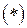 до
до  , отримаємо
, отримаємо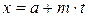 ,
, 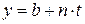 ,
, 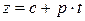 .
.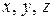 , записані через параметр
, записані через параметр 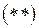 , знайдемо спочатку
, знайдемо спочатку 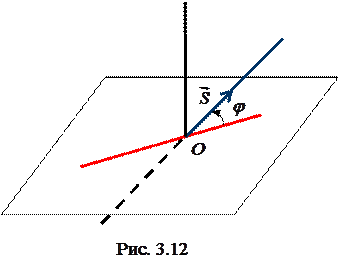 Для розгляду умов паралельності і перпендикулярності прямої і площини знайдемо кут між прямою і площиною.
Для розгляду умов паралельності і перпендикулярності прямої і площини знайдемо кут між прямою і площиною. – кут між прямою і площиною. Його безпосередньо знайти не можна, але можна знайти кут між направляючим вектором прямої і нормальним вектором площини і, віднявши його від
– кут між прямою і площиною. Його безпосередньо знайти не можна, але можна знайти кут між направляючим вектором прямої і нормальним вектором площини і, віднявши його від 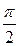 , визначимо
, визначимо  ,
, 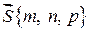 , маємо
, маємо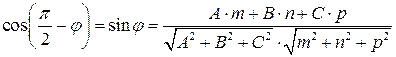 .
.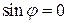 , а це значить, що
, а це значить, що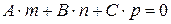 – умова паралельності прямої і площини.
– умова паралельності прямої і площини.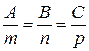 .
.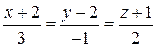 і площини
і площини  .
. .
.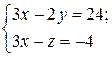 і площиною
і площиною 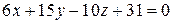 .
. .
.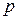 , щоб пряма
, щоб пряма  була паралельна площини
була паралельна площини  .
. .
.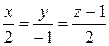 площину, паралельну прямій
площину, паралельну прямій 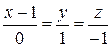 .
.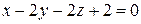 .
.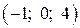 провести пряму, паралельну площини
провести пряму, паралельну площини 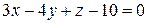 так, щоб вона перетинала пряму
так, щоб вона перетинала пряму 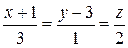 .
. .
.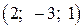 і пряму
і пряму 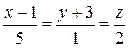 .
.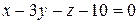 .
.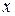 і
і 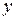 може містити члени другого степеня
може містити члени другого степеня 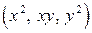 , першого степеня
, першого степеня 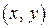 , а також нульового степеня (вільний член).
, а також нульового степеня (вільний член).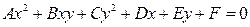 , (1)
, (1)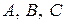 рівняння (1) не дорівнює нулю.
рівняння (1) не дорівнює нулю.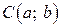 і радіуса
і радіуса 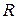 має рівняння:
має рівняння: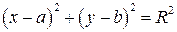 . (2)
. (2) Еліпсом називається геометричне місце точок, сума відстаней яких до двох даних точок, що називаються фокусами, є величина стала і більша від відстані між фокусами (рис. 3.13).
Еліпсом називається геометричне місце точок, сума відстаней яких до двох даних точок, що називаються фокусами, є величина стала і більша від відстані між фокусами (рис. 3.13).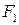 і
і 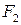 , а початок координат знаходився в середині відрізка
, а початок координат знаходився в середині відрізка 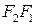 .
.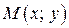 одна з точок розглянутої множини. Позначимо через
одна з точок розглянутої множини. Позначимо через  відстань між заданими точками
відстань між заданими точками 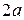 задану суму відстаней
задану суму відстаней 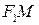 і
і 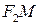 . Точка
. Точка  , точка
, точка 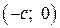 .
.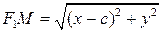 ,
, 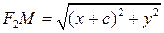 .
.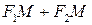 – є величина стала, рівна
– є величина стала, рівна  , (3)
, (3)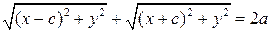 ;
;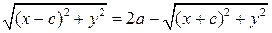 ;
;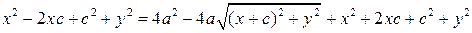 ,
, ;
;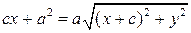 ;
;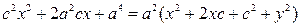 ;
; ;
; .
. , одержимо:
, одержимо: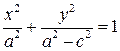 .
. Оскільки
Оскільки  (сума двох сторін трикутника більше
(сума двох сторін трикутника більше 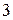 - ї сторони), то
- ї сторони), то  .
. . (4)
. (4)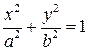 . (5)
. (5)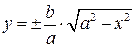 і
і  , то крива симетрична відносно осей координат, а тому і відносно початку координат. Зі зростанням
, то крива симетрична відносно осей координат, а тому і відносно початку координат. Зі зростанням 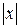 від
від  до
до 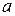 ,
, 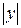 спадає від
спадає від 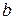 до
до 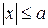 ,
, 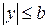 . Точка перетину осей симетрії – центр симетрії, вона називається центром еліпса.
. Точка перетину осей симетрії – центр симетрії, вона називається центром еліпса.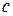 змінюється форма еліпса. Якщо
змінюється форма еліпса. Якщо 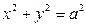 , тобто коло є частинний випадок еліпса, коли півосі еліпса рівні між собою.
, тобто коло є частинний випадок еліпса, коли півосі еліпса рівні між собою. прямує до нуля, і, отже, еліпс стискується уздовж осі ординат. Отже, відношення
прямує до нуля, і, отже, еліпс стискується уздовж осі ординат. Отже, відношення 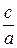 може служити мірою еліпса, мірою його відхилення від кола.
може служити мірою еліпса, мірою його відхилення від кола.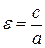
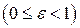 називається ексцентриситетом еліпса.
називається ексцентриситетом еліпса.