 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Алгоритм обчислення оберненої матриці
1). Знаходимо визначник даної матриці. Якщо 2). Знаходимо алгебраїчні доповнення до елементів даної матриці 3). Складаємо приєднану матрицю 4). Обчислюємо обернену матрицю за формулою (2). 5). Перевіряємо правильність обчислення оберненої матриці
Приклад. Знайти обернену матрицю: Розв’язання.
1. Визначник матриці
2. Знаходимо алгебраїчні доповнення до елементів матриці
3°. Складаємо приєднану матрицю
4°. Обчислюємо обернену матрицю
5°. Перевіряємо правильність обчислення оберненої матриці за формулою:
Для невироджених матриць виконуються наступні властивості: 1). 2). 3). 4). 5).
Ранг матриці. Властивості рангу Для розв’язання і дослідження ряду математичних і прикладних задач важливе значення має поняття рангу матриці. У матриці Серед усіх відмінних від нуля мінорів матриці
Означення. Рангом матриці Ранг матриці З означення випливає: а) ранг матриці б) в) для квадратної матриці Приклад. Обчислити ранг матриці: Розв’язання. Матриця
Елементарні перетворення матриці. Обчислення рангу матриці
Поиск по сайту: |
 , то матриця
, то матриця 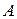 – вироджена і оберненої матриці
– вироджена і оберненої матриці  не існує. Якщо
не існує. Якщо 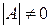 , то матриця
, то матриця 
 .
. , шляхом транспонування алгебраїчних доповнень
, шляхом транспонування алгебраїчних доповнень 
 .
. .
. , тобто матриця
, тобто матриця  ;
;  ;
;  ;
; 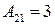 ;
;  ;
;  ;
;  ;
;  ;
;  .
.
 .
.
 .
. ;
; ;
; ;
; ;
; .
. викреслюванням будь-яких рядків і стовпців можна отримати квадратні підматриці
викреслюванням будь-яких рядків і стовпців можна отримати квадратні підматриці 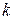 - го порядку, де
- го порядку, де  . Очевидно, що матриця
. Очевидно, що матриця  до найменшого з чисел
до найменшого з чисел 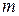 і
і 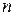 .
. , або
, або 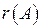 .
. не перевищує меншого з її розмірів, тобто
не перевищує меншого з її розмірів, тобто  ;
; тоді і тільки тоді, коли всі елементи матриці дорівнюють нулю, тобто
тоді і тільки тоді, коли всі елементи матриці дорівнюють нулю, тобто  ;
; тоді і тільки тоді, коли матриця
тоді і тільки тоді, коли матриця  .
. . Однак
. Однак 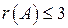 . Усі підматриці третього порядку теж містять нульовий стовпець і тому мають нульові визначники, отже
. Усі підматриці третього порядку теж містять нульовий стовпець і тому мають нульові визначники, отже  . Усі підматриці другого порядку або мають нульовий стовпець (другий або четвертий), або мають пропорційні стовпці (перший і третій), тому теж мають нульові визначники; таким чином
. Усі підматриці другого порядку або мають нульовий стовпець (другий або четвертий), або мають пропорційні стовпці (перший і третій), тому теж мають нульові визначники; таким чином  . Оскільки матриця
. Оскільки матриця  .
.