|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Системи лінійних рівнянь. Основні поняття і означення
Система
де У більш короткому записі за допомогою знаків підсумовування систему можна записати у виді:
Розв’язком системи (2) називається така сукупність Система рівнянь називається сумісною, якщо вона має хоча б один розв’язок, і несумісною, якщо вона не має розв’язків. Сумісна система рівнянь називається визначеною, якщо вона має єдиний розв’язок, і невизначеною, якщо вона має більш одного розв’язку. Наприклад, система рівнянь Система Дві системи рівнянь називаються рівносильними, або еквівалентними, якщо вони мають однакову множину розв’язків. Запишемо систему (1) у матричній формі. Позначимо:
де Оскільки число стовпців матриці
є матриця-стовпець. Елементами отриманої матриці є ліві частини системи (1). На основі визначення рівності матриць систему (1) можна записати у виді
1.5.2. Система
Нехай число рівнянь системи (1) дорівнює числу змінних, тобто Розглянемо розв’язок системи двох рівнянь із двома змінними:
у якій хоча б один з коефіцієнтів при змінних відмінний від нуля. Для розв’язання цієї системи виключимо змінну
Вираз в дужках є визначником системи
Позначивши
З отриманої системи випливає, що якщо визначник системи
Якщо Якщо Для одержання розв’язку системи (1) при Помноживши зліваобидві частини матричної рівності (3) на матрицю
Теорема Крамера. Нехай
Формули (8) отримали назва формул Крамера. Доведення. Обернена матриця обчислюється за формулою
Враховуючи, що
звідки випливає, що для будь-якого
На основі властивості визначників (властивість 10) Формули Крамера фактично були отримані в окремому випадку при розв’язанні системи (4) при
Приклад. Розв’язати систему рівнянь а) методом оберненої матриці; б) за формулами Крамера. Розв’язання. а) Позначимо Тоді в матричній формі дана система має вигляд: Матрицю
Тепер за формулою (7)
б) Знайдемо визначник системи Обчислимо визначники матриць
Відповідь: Істотним недоліком розв’язання систем
Метод Гаусса Метод Гаусса Розглянемо розв’язок системи
Метод Гаусса – метод послідовного виключення змінних полягає в тому, що за допомогою елементарних перетворень система рівнянь приводиться до рівносильної системи східчастого (або трикутного) виду з якої, послідовно, починаючи з останніх (за номером) змінних знаходяться всі інші змінні. Це історично перший найбільш розповсюджений точний метод розв’язання систем лінійних рівнянь. Легко перевірити, що елементарні перетворення приводять дану систему рівнянь в еквівалентну систему. Припустимо що в системі (1) коефіцієнт при змінній Крок 1. Помноживши перше рівняння на підходящі числа (а саме на
де буквами з верхнім індексом (1) позначені нові коефіцієнти, отримані після першого кроку. Крок 2. Припустимо що Помножимо друге рівняння на підходящі числа Продовжуючи процес послідовного виключення змінних
Число нуль в останніх
Якщо хоча б одне з чисел Таким чином, для будь-якої сумісної системи числа У цьому випадку останні а) число рівнянь системи (3) дорівнює числу змінних тобто б) Перехід системи (1) до рівносильної їй системи (3) називається прямим ходомметоду Гаусса, а знаходження змінних із системи (3) – зворотним ходом. Перетворення Гаусса зручно проводити, здійснюючи перетворення не із самими рівняннями, а з матрицями їхніх коефіцієнтів. Така матриця має вигляд
і називається розширеною матрицею системи (1), тому що в неї, окрім матриці системи
Поиск по сайту: |
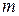 лінійних рівнянь з
лінійних рівнянь з 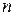 змінними має вигляд:
змінними має вигляд: (1)
(1)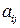 ,
, 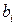
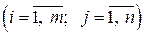 – довільні числа, які називаються відповідно коефіцієнтами при змінних і вільних членах рівнянь.
– довільні числа, які називаються відповідно коефіцієнтами при змінних і вільних членах рівнянь.
 . (2)
. (2)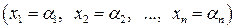 , при підстановці яких кожне рівняння системи обертається у правильну рівність.
, при підстановці яких кожне рівняння системи обертається у правильну рівність.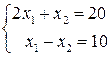 – сумісна і визначена, тому що має єдиний розв’язок
– сумісна і визначена, тому що має єдиний розв’язок 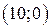 .
. – несумісна, а система рівнянь
– несумісна, а система рівнянь 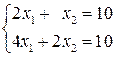 – сумісна і невизначена, тому що має більш одного розв’язку, а точніше нескінченну множину розв’язків
– сумісна і невизначена, тому що має більш одного розв’язку, а точніше нескінченну множину розв’язків 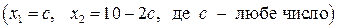 .
.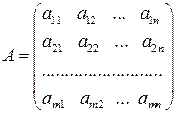 ;
;  ;
; 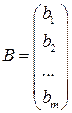 ,
,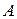 – матриця з коефіцієнтів при змінних, або матриця системи;
– матриця з коефіцієнтів при змінних, або матриця системи;  – матриця-стовпець змінних;
– матриця-стовпець змінних; 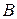 – матриця-стовпець вільних членів.
– матриця-стовпець вільних членів. дорівнює числу рядків матриці
дорівнює числу рядків матриці 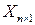 , то їх добуток
, то їх добуток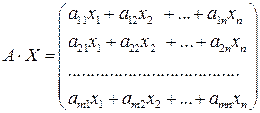
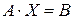 . (3)
. (3) . Тоді матриця системи є квадратна, а її визначник
. Тоді матриця системи є квадратна, а її визначник  називається визначником системи.
називається визначником системи. , (4)
, (4)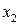 , помноживши перше рівняння на
, помноживши перше рівняння на 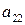 , друге – на
, друге – на  і додамо їх. Потім виключимо змінну
і додамо їх. Потім виключимо змінну  , помноживши перше рівняння на
, помноживши перше рівняння на  , друге – на
, друге – на 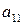 і також додамо їх. У результаті одержимо систему:
і також додамо їх. У результаті одержимо систему: . (5)
. (5)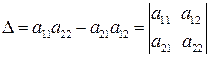 .
.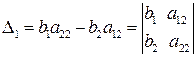 ,
,  система (5) прийме вид:
система (5) прийме вид: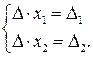 (6)
(6)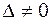 , то система (4) має єдиний розв’язок, визначений за формулами:
, то система (4) має єдиний розв’язок, визначений за формулами: ,
, 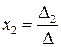 .
.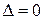 , а
, а 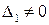 (або
(або  ), то система (4) несумісна, тому що в цьому випадку приводиться до виду:
), то система (4) несумісна, тому що в цьому випадку приводиться до виду:  .
.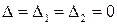 , то система (4) невизначена і має нескінченну множину розв’язків, тому що в цьому випадку приводиться до виду:
, то система (4) невизначена і має нескінченну множину розв’язків, тому що в цьому випадку приводиться до виду: 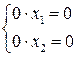 .
.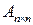 невироджена, тобто її визначник
невироджена, тобто її визначник 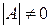 . У цьому випадку існує обернена матриця
. У цьому випадку існує обернена матриця  .
.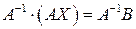 . Оскільки
. Оскільки  , то розв’язком системи методом оберненої матриці буде матриця-стовпець
, то розв’язком системи методом оберненої матриці буде матриця-стовпець . (7)
. (7) – визначник матриці
– визначник матриці 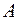 системи, а
системи, а 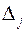 – визначник матриці, отриманий з матриці
– визначник матриці, отриманий з матриці 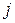 -го стовпця стовпцем вільних членів. Тоді, якщо
-го стовпця стовпцем вільних членів. Тоді, якщо 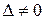 , то система має єдиний розв’язок, визначений за формулами:
, то система має єдиний розв’язок, визначений за формулами:
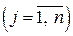 . (8)
. (8)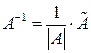 , де
, де 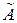 – матриця приєднана до матриці
– матриця приєднана до матриці 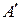 , транспонованої до
, транспонованої до 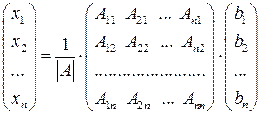 .
.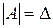 , одержимо після множення матриць
, одержимо після множення матриць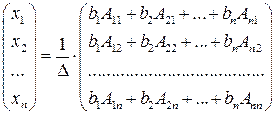 ,
,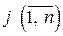
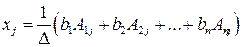 .
.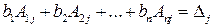 , де
, де 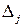 – визначник матриці, отриманий з матриці
– визначник матриці, отриманий з матриці 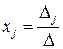 .
.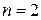 .
.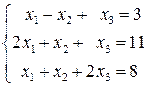
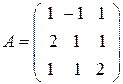 ;
; 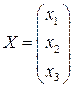 ;
; 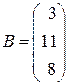 .
. . Знайдемо визначник
. Знайдемо визначник 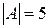 . Оскільки
. Оскільки 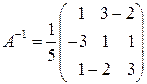 .
. , тобто розв’язок системи
, тобто розв’язок системи 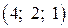 .
.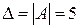 . Оскільки
. Оскільки 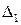 ,
,  ,
, 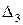 , отримані з матриці
, отримані з матриці 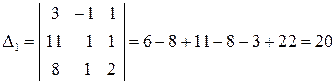 ;
;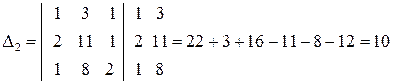 ;
;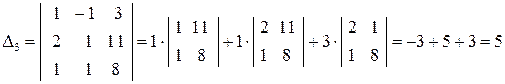 .
. ;
; 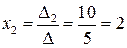 ;
; 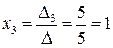 .
. (1)
(1)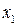 у першому рівнянні
у першому рівнянні 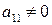
 (якщо це не так, то перестановкою рівнянь місцями досягнемо того, що
(якщо це не так, то перестановкою рівнянь місцями досягнемо того, що 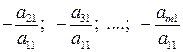 ) і додаючи отримані рівняння відповідно до другого, третього, …,
) і додаючи отримані рівняння відповідно до другого, третього, …,  (2)
(2) (якщо це не так то відповідною перестановкою рівнянь або змінних зі зміною їх номерів досягнемо того щоб
(якщо це не так то відповідною перестановкою рівнянь або змінних зі зміною їх номерів досягнемо того щоб  ).
). і додаючи отримані рівняння відповідно до третього, четвертого, …,
і додаючи отримані рівняння відповідно до третього, четвертого, …,  після
після 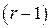 -го кроку одержимо систему:
-го кроку одержимо систему: (3)
(3)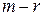 рівняннях означає, що їх ліві частини мають вигляд
рівняннях означає, що їх ліві частини мають вигляд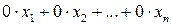 .
.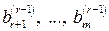 не дорівнює нулю, то відповідна рівність суперечлива, і система (1) несумісна.
не дорівнює нулю, то відповідна рівність суперечлива, і система (1) несумісна.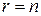 (у цьому випадку система (3) має трикутний вигляд);
(у цьому випадку система (3) має трикутний вигляд);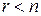 (у цьому випадку система (3) має східчастий вигляд).
(у цьому випадку система (3) має східчастий вигляд).