 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Умови сумісності і несумісності лінійних систем. Теорема Кронекера-Капеллі
Дослідимо в загальному виді довільну систему Розглянемо матрицю
Ясно, що ранги цих матриць зв’язані нерівністю
Було встановлено, що ранг матриці дорівнює максимальному числу її лінійно незалежних рядків. Тому, якщо рядки розширеної матриці Питання про сумісність системи (1) цілком у загальному виді розглядається наступною теоремою. Теорема Кронекера-Капеллі. Для того щоб система лінійних рівнянь була сумісна, необхідно і достатньо, щоб ранг матриці цієї системи дорівнював рангу її розширеної матриці.
Доведення. Необхідність.Нехай система (1) сумісна і
У розширеній матриці
У силу (2) останній стовпець (3) складається з нулів. Тому що матриця Достатність. Припустимо, що ранги матриць Нехай ранг матриці
(Це завжди можна зробити за допомогою зміни нумерації невідомих і перестановок рівнянь у системі). Виділимо в системі (1) перші
Помітимо, що у випадку Покажемо, що системи (1) і (4) рівносильні (при виконанні умов Той факт, що кожний розв’язок системи (1) (якщо він існує) є також і розв’язком системи (4), очевидний. Необхідно перевірити, що і, навпаки, кожний розв’язок системи (4), якщо він існує, є також розв’язком системи (1). Нехай
Числа
Розглянемо розширену матрицю системи:
і виконаємо її як і при доведенні необхідності, елементарні перетворення: з останнього стовпці віднімемо всі інші стовпці, помножені відповідно на
Перші Але доведення цих рівностей рівносильні доведенню того, що всі інші елементи останнього стовпця матриці
Тоді матрицю
Матриця отримана з
Розкладаючи цей визначник за елементам останнього стовпця, одержимо:
Але Встановлено, що системи (1) і (4) рівносильні. Питання про існування розв’язків у системі (1) зведено до питання про існування розв’язків у системі (4). Якщо У випадку
Визначник
Сукупність чисел Теорема Кронекера-Капеллі доведена цілком. З доведення теореми Кронекера-Капеллі легко одержати відповідь на питання про число розв’язків (у випадку її сумісності).
Поиск по сайту: |
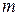 лінійних рівнянь з
лінійних рівнянь з 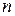 невідомими (1).
невідомими (1).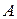 цієї системи і її розширену матрицю
цієї системи і її розширену матрицю 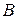 :
: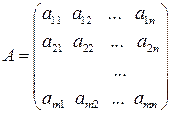
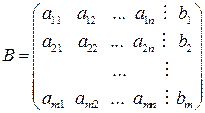 .
.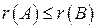 , при цьому ранг матриці
, при цьому ранг матриці 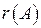 .
. , якщо лінійно залежні, то
, якщо лінійно залежні, то  .
. – який-небудь її розв’язок. Тоді мають місце рівності:
– який-небудь її розв’язок. Тоді мають місце рівності: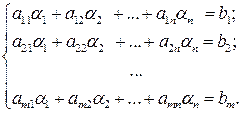 (2)
(2) , другий, помножений на
, другий, помножений на  і т.д., нарешті на
і т.д., нарешті на  . Одержимо матрицю:
. Одержимо матрицю: . (3)
. (3) виходить із
виходить із  . З іншого боку,
. З іншого боку,  . Отже,
. Отже,  і необхідна умова теореми доведена.
і необхідна умова теореми доведена. . Серед мінорів
. Серед мінорів 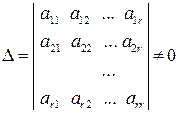 .
. (4)
(4) ).
). (5)
(5) рівнянням, тобто, що при
рівнянням, тобто, що при  справедливі рівності:
справедливі рівності: . (6)
. (6)
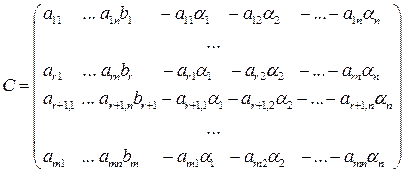
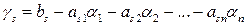 . (7)
. (7)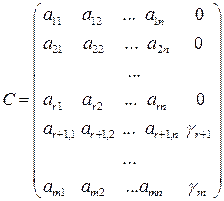 .
.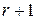 дорівнюють нулю. Зокрема, дорівнює нулю і мінор
дорівнюють нулю. Зокрема, дорівнює нулю і мінор 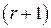 -го порядку, складений зі стовпців з номерами
-го порядку, складений зі стовпців з номерами 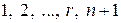 і з рядків з номерами
і з рядків з номерами 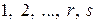 (де
(де  -будь-які з чисел
-будь-які з чисел 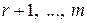 ), тобто
), тобто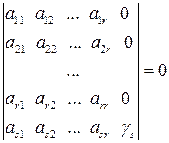 .
.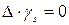 .
.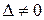 , тому отримана нерівність свідчить про те, що
, тому отримана нерівність свідчить про те, що 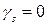 . Таким чином, усі числа (7) дорівнюють нулю, а отже, справедливі рівності (6). Це доводить, що всякий розв’язок системи (4) задовольняє всім рівнянням системи (1).
. Таким чином, усі числа (7) дорівнюють нулю, а отже, справедливі рівності (6). Це доводить, що всякий розв’язок системи (4) задовольняє всім рівнянням системи (1).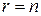 , то система (4) є система
, то система (4) є система 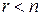 невідомим
невідомим 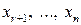 надамо довільні значення
надамо довільні значення 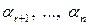 , і розглянемо систему:
, і розглянемо систему: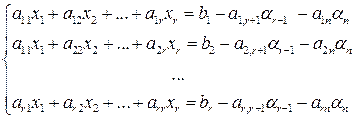 .
. цієї системи
цієї системи 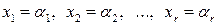 .
.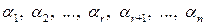 буде, мабуть, розв’язком системи (4). Так що в цьому випадку система (4) має нескінченну множину розв’язків (адже значення для невідомих
буде, мабуть, розв’язком системи (4). Так що в цьому випадку система (4) має нескінченну множину розв’язків (адже значення для невідомих 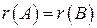 , то система (1) сумісна.
, то система (1) сумісна.