 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Зв’язок між розв’язками однорідних і неоднорідних систем рівнянь
Встановимо зв’язок між розв’язками однорідних і неоднорідних систем рівнянь. Нехай задана система неоднорідних лінійних рівнянь
Систему однорідних рівнянь (1), що одержимо із системи(2), унаслідок заміни вільних членів нулями, називають приведеною системою для системи (2). Залежність між розв’язками систем (1) і (2) виражається наступними теоремами:
Теорема. Сума довільного розв’язку (2) і розв’язку (1) є розв’язком системи (2). Доведення. Дійсно, нехай
Теорема доведена. Теорема. Різниця двох довільних розв’язків системи (2) є розв’язком приведеної системи (1). Доведення. Дійсно, нехай
Теорема доведена. З теорем випливає: визначивши деякий частинний розв’язок системи неоднорідних рівнянь (2) і склавши з ним кожний розв’язок приведеної системи (1), одержимо всі розв’язки системи (2). Таким чином, загальний розв’язок неоднорідної системи (2) дорівнює сумі якого-небудь частинного розв’язку цієї системи і загального розв’язку приведеної системи (1).
Приклад. Знайти загальний розв’язок і фундаментальну систему розв’язків однорідної системи.
Розв’язання.
Запишемо перші два рівняння системи:
Загальний розв’язок системи буде:
Розглянемо вектори Тоді
Отже, розв’язки Питання для самоконтролю: 1. Матриці. Основні поняття. Види матриць. 2. Дії з матрицями. 3. Визначники квадратних матриць. Визначники 2-го та 3-го порядку. 4. Мінори і алгебраїчні доповнення. 5. Властивості визначників. 6. Особливі і неособливі матриці. Обернена матриця. 7. Ранг матриці. Властивості рангу. 8. Елементарні перетворення матриці. Обчислення рангу матриці. 9. Системи лінійних рівнянь. Основні поняття і означення. 10. Система лінійних рівнянь з 11. Метод Гаусса. 12. Система 13. Умови сумісності та несумісності лінійних систем. Теорема Кронекера-Капеллі. 14. Однорідні системи лінійних рівнянь. Теорема про наявність ненульового розв’язку однорідної системи. 15. Зв’язок між розв’язками неоднорідних та однорідних систем рівнянь.
Тести до розділу 1 1. Дано матриці 1) 2. Дано матриці: 3. Дана матриця Відповідь: 4. Дана матриця 5. З’ясувати, які з наведених нижче матриць мають обернені: 1) 6. При якім значенні 7. Знайти суму діагональних елементів матриці 8. Розташувати матриці в порядку спадання їх рангів: 1) 9. Скільки лінійно незалежних рядків має матриця
10. Розв’язати рівняння:
Відповіді: 1.
Поиск по сайту: |
 (2)
(2)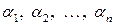 – розв’язок системи (2),
– розв’язок системи (2),  – розв’язок системи (1). Візьмемо яке-небудь рівняння системи (2), наприклад
– розв’язок системи (1). Візьмемо яке-небудь рівняння системи (2), наприклад 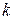 - е і підставимо в нього замість змінних числа
- е і підставимо в нього замість змінних числа  . Отримаємо
. Отримаємо .
. розв’язки системи (2). Візьмемо яке-небудь рівняння системи (1), наприклад
розв’язки системи (2). Візьмемо яке-небудь рівняння системи (1), наприклад  . Отримаємо
. Отримаємо .
.
 .
. .
.
 , тоді
, тоді 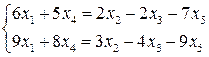

 ,
, 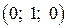 і
і 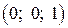 .
.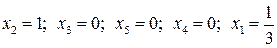 ,
,
 .
.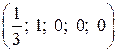 ,
,  і
і  є фундаментальними розв’язками системи розв’язків.
є фундаментальними розв’язками системи розв’язків.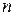 невідомими. Матричний метод і формули Крамера для розв’язання систем лінійних рівнянь.
невідомими. Матричний метод і формули Крамера для розв’язання систем лінійних рівнянь.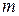 лінійних рівнянь з
лінійних рівнянь з  і
і  . З’ясувати, які з наступних операцій можна виконувати:
. З’ясувати, які з наступних операцій можна виконувати: ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5) 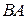 ; 6)
; 6)  ; 7)
; 7)  ; 8)
; 8)  ; 9)
; 9)  .
. ;
; 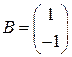 . Знайти
. Знайти  .
. . Знайти матрицю
. Знайти матрицю  .
. , де
, де  ;
; 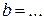 ;
;  ;
; 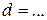 .
.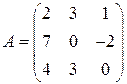 . Знайти визначник
. Знайти визначник  матриці
матриці  .
. ; 2)
; 2) 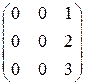 ; 3)
; 3)  ; 4)
; 4)  .
.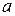 матриця
матриця 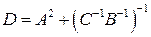 буде дорівнювати матриці
буде дорівнювати матриці  , де
, де  ?
? , де
, де  ;
;  ;
;  .
.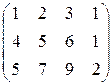 ; 2)
; 2) 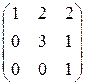 ; 3)
; 3)  ; 4)
; 4)  .
. , де
, де ;
;  ;
;  ?
? .
.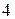 ;
; 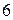 ;
;  . 2.
. 2. 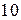 . 3.
. 3.  ;
; 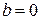 ;
; 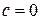 ;
;  . 4.
. 4.  . 5.
. 5.  . 6.
. 6.  ;
;  ;
;  ;
;