 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Властивості мішаного добутку векторів
1. ♦ Мішаний добуток дорівнює нулю тоді, і тільки тоді, коли співмножники компланарні. 2. ♦ Якщо в правому в ортонормованому базисі
3. ♦ Базис 4. ♦ Якщо в мішаному добутку два множники однакові, то він дорівнює 5. ♦ Якщо вектори записані у вигляді:
6. ♦ Об’єм паралелепіпеду, побудованого на некомпланарних векторах 7. ♦ Мішаний добуток лінійний по кожному з співмножників.
2.3.4. Мішаний добуток векторів в координатній формі. Умова компланарності векторів Нехай дані вектори
Знаючи проекції векторного добутку
Права частина цієї рівності являє собою розклад визначника третього порядку
Використовуючи
Задача. Дано координати вершин піраміди: Потрібно: 1) записати вектори Розв’язання. 1. Відомо, що довільний вектор
де Якщо дані точки
і
Підставляючи в (3) координати точок
Аналогічно, підставивши в (3) координати точок
Відомо, що модуль вектора
Застосовуючи (4), одержимо:
2. Відомо, що косинус кута між двома векторами дорівнює скалярному добуткові цих, векторів, поділеному на добуток їхніх модулів. Отже,
3. Запишемо скалярний добуток векторів
Оскільки добуток
відкіля
Вектори
Таким чином, проекція вектора 4. Площа грані Отже, площа грані
Відомо, що об’єм паралелепіпеда, побудованого на трьох некомпланарних векторах, дорівнює абсолютній величині їхнього мішаного добутку. Якщо вектори, що перемножуються, розкладені по ортонормованому базису
то мішаний добуток цих векторів знаходиться за формулою
Застосовуючи (6), визначимо мішаний добуток векторів
Отже, об’єм паралелепіпеда, побудованого на векторах
Питання для самоконтролю: 1. Скалярні та векторні величини. Лінійні дії з векторами: додавання, віднімання, множення вектора на число. Проекції вектора на осі. 2. Лінійна залежність та незалежність векторів. Базис. Розкладання вектора по ортонормованому базису. Довжина вектора. Напрямні косинуси вектора. 3. Лінійні дії з векторами, заданими розкладом в ортонормованому базисі. Поділ відрізка в даному відношенні. Умови колініарності векторів. 4. Скалярний добуток векторів, його означення, фізичний зміст, властивості. 5. Скалярний добуток векторів в координатній формі. Умови перпендикулярності двох векторів. Кут між векторами. 6. Векторний добуток векторів, його означення, фізичний зміст, властивості. 7. Векторний добуток векторів в координатній формі. 8. Мішаний добуток векторів, його геометричний зміст і властивості. 9. Мішаний добуток векторів в координатній формі. Умова компланарності трьох векторів.
Тести до розділу 2 1. Вказати формулу скалярного добутку векторів, заданих координатами: а) 2. Вказати формулу косинуса кута між векторами а) 3. Якими повинні бути вектори
4. З’ясувати, які з наведених трійок векторів утворюють базис в просторі 1) 2) 3) 5. Дано точки 6. При якому значенні 7. Знайти кут між діагоналями паралелограма, побудованого на векторах 8. Знайти роботу сили 9. Обчислити площу трикутника 10. Знайти об’єм паралелепіпеда, побудованого на векторах
Відповіді: 1.
Поиск по сайту: |
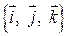 , вектори
, вектори  ,
, 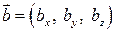 ,
, 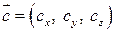 , то мішаний добуток векторів
, то мішаний добуток векторів
 .
. є правим тоді і тільки тоді, коли мішаний добуток
є правим тоді і тільки тоді, коли мішаний добуток  .
. .
. ;
; 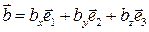 ;
; 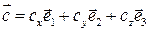 , то
, то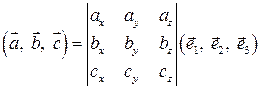 .
. ,
, 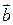 ,
, 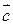 , (рис. 2.12) дорівнює модулю мішаного добутку цих векторів.
, (рис. 2.12) дорівнює модулю мішаного добутку цих векторів.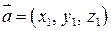 ,
, 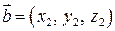 ,
, 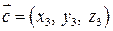 .Знайдемо спочатку проекції векторного добутку
.Знайдемо спочатку проекції векторного добутку 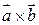 , вони дорівнюють:
, вони дорівнюють: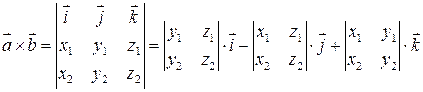 ;
;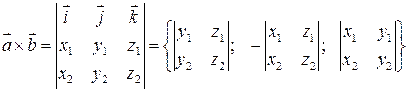 .
.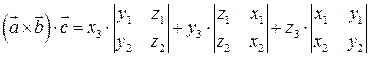 .
.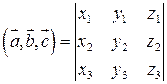 .
. 
 .
. ,
, 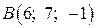 ,
,  ,
,  .
.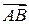 ,
, 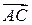 і
і 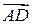 в системі орт і знайти модулі цих векторів; 2) знайти кут між векторами
в системі орт і знайти модулі цих векторів; 2) знайти кут між векторами  ; 5) знайти об’єм піраміди
; 5) знайти об’єм піраміди  .
.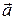 може бути представлений у системі орт
може бути представлений у системі орт  ,
, 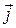 ,
, 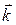 за формулою:
за формулою: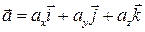 , (1)
, (1)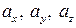 – проекції вектора
– проекції вектора  , а
, а 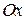 ,
, 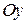 і
і 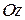 .
.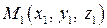 і
і 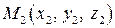 , то проекції вектора
, то проекції вектора 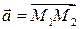 на координатні осі знаходяться за формулами:
на координатні осі знаходяться за формулами: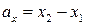 ;
; 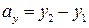 ;
; 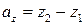 (2)
(2)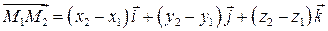 . (3)
. (3)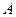 і
і  , одержимо:
, одержимо: .
.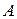 і
і 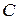 знаходимо:
знаходимо: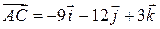 ,
, , знаходимо:
, знаходимо: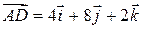 .
. , заданого в системі орт формулою (1), обчислюєтьсяза формулою:
, заданого в системі орт формулою (1), обчислюєтьсяза формулою: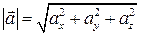 . (4)
. (4) ;
; ;
;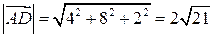 .
.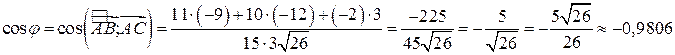
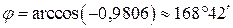 .
.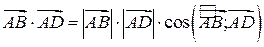 .
.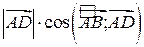 виражає собою проекцію вектора
виражає собою проекцію вектора 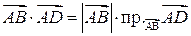 ,
,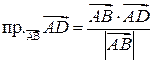 .
.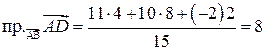 .
. .
. . Тоді, як відомо, модуль вектора
. Тоді, як відомо, модуль вектора 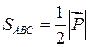 .
.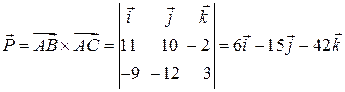 ;
;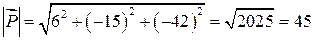 ;
;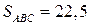 (од.2)
(од.2)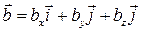 ;
;  ,
,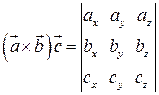 . (6)
. (6) .
. . Оскільки об’єм
. Оскільки об’єм  шуканої піраміди
шуканої піраміди 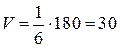 .
.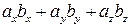 ; б)
; б) 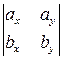 ; в)
; в) 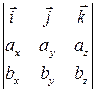 .
.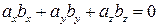 ; б)
; б) 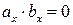 ; в)
; в)  .
. , щоб мало місце співвідношення:
, щоб мало місце співвідношення: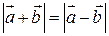 .
.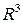 :
: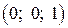 ,
, 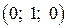 ,
, 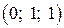 ;
; ,
,  ,
, 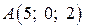 ,
, 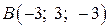 ,
, 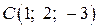 ,
, 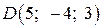 . Чи можуть вони бути вершинами трапеції?
. Чи можуть вони бути вершинами трапеції?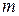 вектори
вектори  і
і 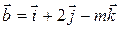 перпендикулярні?
перпендикулярні? ,
, 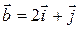 .
.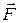 при переміщенні її на відстань
при переміщенні її на відстань 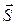 , якщо
, якщо 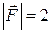 ,
, 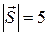 ,
, 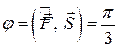 .
. ,
, 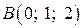 ,
, 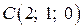 .
. ,
, 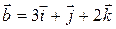 ,
, 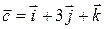 .
. . 2.
. 2.  . 3.
. 3. 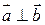 . 4.
. 4. 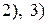 . 5.
. 5.  . 6.
. 6.  . 7.
. 7. 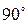 . 8.
. 8.  . 9.
. 9. 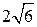 . 10.
. 10.  .
.