 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Приклад 1. Розв’язати систему рівнянь
Розв’язання. Крок 1. Оскільки
В отриманій новій матриці ~ Крок 2. Оскільки тепер ~ Крок 3. Враховуючи, що ~ Перейдемо від матричного запису до запису у виді системи.
Використовуючи зворотний хід методу Гаусса, знайдемо з четвертого рівняння із третього рівняння із другого рівняння з першого рівняння Тобто розв’язком системи є
Приклад 2. Методом Гаусса розв’язати систему рівнянь
Розв’язання. Перетворимо розширену матрицю системи:
Отже, рівняння, що відповідає третьому рядку матриці, суперечливе, воно привелося до невірної рівності
1.7. Система 1.7.1. Система Система
У загальному випадку число рівнянь у системі не обов’язково співпадає з числом невідомих: Числа Розглянемо декілька прикладів.
Приклад 1.
Ця система двох рівнянь із трьома невідомими розв’язків не має, тому що будь-яка трійка чисел, що задовольняє першому рівнянню, не може задовольняти другому.
Приклад 2.
Легко бачити, що ця система має єдиний розв’язок:
Приклад 3.
Пара чисел
Наведені приклади систем показують, що, узагалі кажучи, система може або зовсім не мати розв’язків, або мати єдиний розв’язок, або мати їх множину. Відносно кожної системи лінійних рівнянь можуть бути поставлені наступні питання: 1 Сумісна чи ні задана система? 2 У випадку, якщо система сумісна, як визначити, скільки вона має розв’язків – один або множину? 3 Як знайти всі розв’язки системи?
Відповіді на ці питання дає теорія лінійних рівнянь.
Поиск по сайту: |
 .
.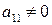 , то помноживши перший рядок матриці на
, то помноживши перший рядок матриці на  ,
,  ,
,  з усіх рядків, починаючи з другого
з усіх рядків, починаючи з другого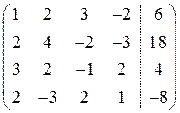 ~
~ 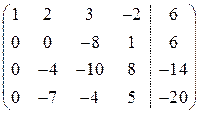 ~
~ , тому поміняємо місцями другий і третій рядки.
, тому поміняємо місцями другий і третій рядки. ~
~  ~
~ , то помноживши другий рядок на
, то помноживши другий рядок на  , а четвертий на
, а четвертий на 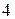 і складаючи, одержимо
і складаючи, одержимо ~
~ , множимо третій рядок на
, множимо третій рядок на 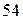 , а четвертий на
, а четвертий на  і складаємо, одержимо
і складаємо, одержимо .
.
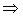
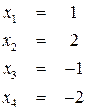 .
. ,
,
 ,
,
 ,
,
 .
.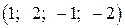 .
.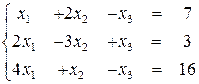 .
.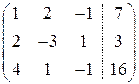 ~
~ 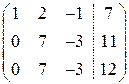 ~
~  .
. , тому дана система несумісна.
, тому дана система несумісна. лінійних рівнянь з
лінійних рівнянь з 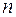 невідомими. Умови сумісності і несумісності лінійних систем. Теорема Кронекера-Капеллі
невідомими. Умови сумісності і несумісності лінійних систем. Теорема Кронекера-Капеллі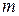 лінійних рівнянь з
лінійних рівнянь з 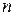 невідомими. На які питання дає відповіді теорія лінійних рівнянь
невідомими. На які питання дає відповіді теорія лінійних рівнянь (1)
(1)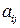 (дійсні або комплексні) називаються коефіцієнтами системи;
(дійсні або комплексні) називаються коефіцієнтами системи; 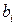 – вільними членами;
– вільними членами;  – невідомими.
– невідомими.

 ,
,  .
.
 є одним з розв’язків цієї системи трьох рівнянь із двома невідомими;
є одним з розв’язків цієї системи трьох рівнянь із двома невідомими;  – інший розв’язок. Ця система має нескінченно багато розв’язків: значення
– інший розв’язок. Ця система має нескінченно багато розв’язків: значення  ,
, 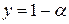 при кожнім
при кожнім  задовольняють системі.
задовольняють системі.