 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Геометричні властивості скалярного добутку
5о. Якщо 6о. Скалярний квадрат вектора дорівнює квадрату його довжини
звідки
Щоб перемножити скалярно два вектори, треба один із них помножити скалярно на одиничний вектор, що має напрям другого і отриманий добуток помножити на довжину другого.
Скалярний добуток векторів в координатній формі. Умови перпендикулярності двох векторів. Кут між векторами Позначимо через
За властивістю дистрибутивності суми векторів перемножуються як многочлени. Отже, матимемо
Оскільки
Скалярний добуток векторів дорівнює сумі добутків однойменних проекцій.
Умова перпендикулярності двох векторів:
тобто
Кут між двома векторами обчислюється зі скалярного добутку векторів
Векторний і мішаний добутки векторів Векторний добуток векторів, його означення, механічний зміст, властивості Векторним добутком двох векторів
Із означення векторного добутку Векторний добуток позначається Векторний добуток дорівнює нульовому вектору в тому і тільки в тому випадку, коли по крайній мірі один з векторів є нульовим, або, якщо ці вектори паралельні (колінеарні). Таким чином, умовою колінеарності векторів є рівність нулю векторного добутку Зауваження. Умову колінеарності двох векторів
Якщо вектори
Якщо сила
Із означення векторного добутку випливає, що величина моменту дорівнює величині сили, помноженої на відстань
Поиск по сайту: |
 і
і  , то
, то  , коли кут
, коли кут  – гострий і
– гострий і  , коли кут
, коли кут  ,
, .
. проекції вектора
проекції вектора 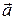 на координатні вісі; а через
на координатні вісі; а через  відповідно проекції вектора
відповідно проекції вектора  . Виразимо скалярний добуток векторів через ці проекції
. Виразимо скалярний добуток векторів через ці проекції .
.
 .
. – три взаємно перпендикулярних одиничних вектора, то
– три взаємно перпендикулярних одиничних вектора, то  ,
,  ,
,  ,
,  ,
,  ,
,  .
. .
. ,
, .
. .
. і
і 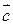 довжина якого чисельно дорівнює площині паралелограма, побудованого на векторах
довжина якого чисельно дорівнює площині паралелограма, побудованого на векторах  Якщо
Якщо  то
то  .
. .
. , або
, або  .
. .
.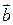 перпендикулярні, то
перпендикулярні, то 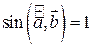 , і тому модуль векторного добутку дорівнює добутку довжин векторів співмножників:
, і тому модуль векторного добутку дорівнює добутку довжин векторів співмножників: , якщо
, якщо 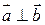 .
.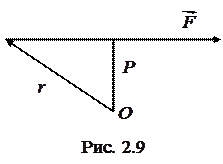 В механіці часто застосовується поняття моменту сили відносно даної точки (рис. 2.9).
В механіці часто застосовується поняття моменту сили відносно даної точки (рис. 2.9). прикладена до точки
прикладена до точки 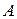 , то моментом сили
, то моментом сили 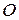 називається вектор
називається вектор  , означений за формулою
, означений за формулою .
.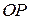 точки
точки