 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Рівняння площини, що проходить через одну і три точки
Вектор, З умови перпендикулярності двох векторів слідує
Нехай на площині
Оскільки усі вектори лежать в одній площині
Одержали рівняння площини, що проходить через три точки.
Кут між площинами. Умови паралельності і перпендикулярності двох площин Нехай задані дві площини
Двогранний кут між площинами визначається лінійним кутом, що дорівнює куту між нормальними векторами
Якщо площини
є умова перпендикулярності площин. Якщо площини
Приклад 1.Скласти рівняння площини, що проходить через точки Розв’язання.Використовуючи дослідження загального рівняння площини, можна записати, що
Тоді
Відповідь:
Приклад 2.Встановити, які з наступних пар рівнянь визначають перпендикулярні площини: 1) 2) 3)
Розв’язання.Перевіряємо для кожної пари площин умову перпендикулярності Отже, а) б) в)
Приклад 3.Скласти рівняння площини, що проходить через початок координат паралельно площині
Розв’язання.Оскільки площина проходить через початок координат, то це означає, що треба використовувати рівняння площини, що проходить через точку:
Оскільки шукана площина паралельна площини
Поиск по сайту: |

 , тоді
, тоді
 , де
, де 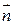 – нормальний вектор площини (рис. 3.8).
– нормальний вектор площини (рис. 3.8). . Прийнявши до уваги, що
. Прийнявши до уваги, що 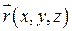 ,
,  ,
,  , і записуючи скалярний добуток векторів у координатній формі, одержимо
, і записуючи скалярний добуток векторів у координатній формі, одержимо 
 – рівняння площини, що проходить через одну точку.
– рівняння площини, що проходить через одну точку. задані три точки
задані три точки  ,
, 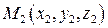 ,
,  , що не лежать на одній прямій (рис. 3.9). Ці точки однозначно визначають площину. Знайдемо її рівняння.
, що не лежать на одній прямій (рис. 3.9). Ці точки однозначно визначають площину. Знайдемо її рівняння. Візьмемо на площині довільну точку
Візьмемо на площині довільну точку  і визначимо вектори:
і визначимо вектори: ,
, ,
,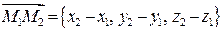 .
. , або
, або  . Це можна записати так:
. Це можна записати так: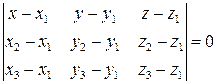 .
. і
і 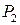 відповідно рівняннями:
відповідно рівняннями:
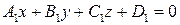 ,
,
 .
. і
і  цих площин. Тоді, використавши формулу скалярного добутку векторів, отримаємо
цих площин. Тоді, використавши формулу скалярного добутку векторів, отримаємо .
.
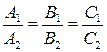 .
. і
і  паралельно осі
паралельно осі 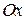 .
.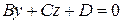 – шукана площина. Підставивши координати точок у це рівняння, отримаємо
– шукана площина. Підставивши координати точок у це рівняння, отримаємо
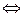


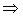
 .
. ,
,  і остаточно
і остаточно .
. і
і  ;
; і
і  ;
; і
і  .
. – площини з пункту 1) перпендикулярні;
– площини з пункту 1) перпендикулярні; – площини з пункту 2) перпендикулярні;
– площини з пункту 2) перпендикулярні; – площини з пункту 3) не перпендикулярні.
– площини з пункту 3) не перпендикулярні. .
. . А оскільки площина проходить через початок координат, то точка
. А оскільки площина проходить через початок координат, то точка  належить площині, значить
належить площині, значить .
. ,
,  ,
, 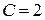 . Тоді
. Тоді 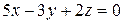 – шукане рівняння площини.
– шукане рівняння площини.