 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Елементарні перетворення матриці. Обчислення рангу матриці
Назвемо елементарними перетвореннями матриці наступні: 1. Відкидання нульового рядка (стовпця). 2. Множення всіх елементів рядка (стовпця) матриці на число, не рівне нулю. 3. Зміна порядку рядків (стовпців) матриці. 4. Додавання до кожного елемента одного рядка (стовпця) відповідних елементів іншого рядка (стовпця), помножених на будь-яке число. 5. Транспонування матриці.
Теорема.Ранг матриці не змінюється при елементарних перетвореннях матриці. При вивченні властивостей визначників було показано, що при перетвореннях квадратних матриць їхні визначники або зберігаються, або множаться на число, не рівне нулю. У результаті зберігається найвищий порядок відмінних від нуля мінорів даної матриці, тобто її ранг не змінюється. За допомогою елементарних перетворень можна привести матрицю до так званого східчастого виду, коли при обчисленні її рангу не виникає труднощів. Матриця
де
Зауваження. Умова Очевидно, що ранг східчастої матриці дорівнює
Дві матриці називаються еквівалентними, якщо одна з них виходить з іншої за допомогою кінцевої множини елементарних перетворень. Еквівалентні матриці не є, узагалі кажучи, рівними, але їхні ранги рівні. Якщо матриці
Канонічною матрицеюназивається матриця, у якої на початку головної діагоналі стоять підряд кілька одиниць (число яких може дорівнювати нулю), а всі інші елементи дорівнюють нулю, наприклад:
За допомогою елементарних перетворень рядків і стовпців будь-яку матрицю можна привести до канонічної. Ранг канонічної матриці дорівнює числу одиниць на її головній діагоналі. Для рангів матриць справедливі наступні співвідношення:
1. 2. 3. 4. 5. 6.
Обчислення рангу методом обведення Викладемо ще один спосіб обчислення рангу матриці, який не потребує приведення її до канонічного виду.
Теорема. Нехай матриця
Поиск по сайту: |
 називається східчастою, якщо вона має вигляд:
називається східчастою, якщо вона має вигляд: , (1)
, (1) ,
, 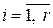 ;
;  .
.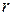 тому що містить мінор
тому що містить мінор 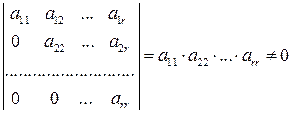 .
.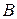 еквівалентні, то це записується так:
еквівалентні, то це записується так:  .
. .
.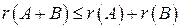 ;
; ;
; ;
; ;
; , якщо
, якщо  ;
; , де
, де 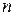 – число стовпців матриці
– число стовпців матриці  порядку
порядку 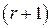 - го порядку матриці
- го порядку матриці