 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Рівняння прямої з кутовим коефіцієнтом. Рівняння прямої, що проходить через дану точку в заданім напрямку. Жмуток прямих
Розглянемо направлений відрізок
Тоді отримаємо: Звідси
(3) – рівняння прямої на площині з кутовим коефіцієнтом. Нехай дана точка Підставивши в це рівняння координати точки Звідси визначимо
Зауваження. Сукупність усіх прямих, що проходять через деяку точку площини, називається жмутком (в’язкою) прямих, а загальна їх точка – центром жмутка. Рівняння прямої, що проходить через дві точки. Рівняння прямої у відрізках Нехай дані точки Рівняння жмутка прямих, що проходять через точку Щоб виділити з цього жмутка пряму, яка проходить через точку
Розв’язавши разом рівняння (4) і (5) і виключивши
Якщо задано вектор
Нехай відомі довжини відрізків
Або поділивши праву частину рівняння почленно і перенісши змінні в ліву частину, матимемо:
Рівняння (7) носить назву рівняння прямої у відрізках.
Нехай прямі Позначимо через Звідси
Замітимо, що
Зауваження 1. Формула (8) визначає тангенс кута, утвореного обертанням навколо точки
Зауваження 2. Якщо не встановлено порядку, в якому розглядаються прямі, то можна встановити цей порядок довільно. При цих змінах порядку може змінюватися знак тангенсу кута.
Зауваження 3. Якщо хоча б одна з прямих паралельна осі
де друга пряма паралельна осі
Поиск по сайту: |
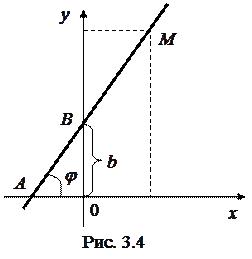 Положення прямої на площині буде цілком визначено, якщо задати кут нахилу прямої до осі абсцис і величину відрізку, відтинаючого нею на осі ординат (рис. 3.4).
Положення прямої на площині буде цілком визначено, якщо задати кут нахилу прямої до осі абсцис і величину відрізку, відтинаючого нею на осі ординат (рис. 3.4).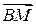 .
. 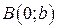 ,
, 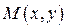 .
. Виразимо проекції
Виразимо проекції 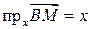 ,
, 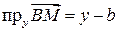 .
. .
.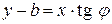 , або
, або 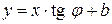 , або
, або 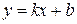 , де
, де 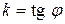 .
. і кутовий коефіцієнт
і кутовий коефіцієнт 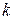 , який визначає напрямок прямої, що проходить через точку
, який визначає напрямок прямої, що проходить через точку 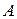 . Рівняння цієї прямої будемо відшукувати у вигляді
. Рівняння цієї прямої будемо відшукувати у вигляді 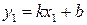 .
.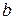 :
: 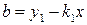 . Тоді
. Тоді 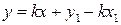

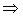
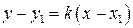 . (4)
. (4)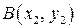 . Складемо рівняння прямої, що проходить через ці точки.
. Складемо рівняння прямої, що проходить через ці точки.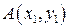 має вигляд (4).
має вигляд (4). (5)
(5) (6)
(6)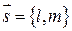 , паралельний деякій прямій, і точку
, паралельний деякій прямій, і точку 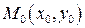 на цій прямій, то рівняння прямої можна записати у вигляді
на цій прямій, то рівняння прямої можна записати у вигляді .
.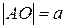 ,
, 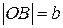 . Тоді точка
. Тоді точка 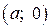 , а точка
, а точка 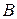 –
–  . Скориставшись формулою (6), отримаємо:
. Скориставшись формулою (6), отримаємо: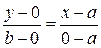 .
. . (7)
. (7)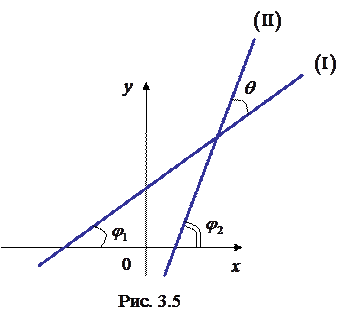 3.1.4. Кут між двома прямими
3.1.4. Кут між двома прямими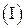 і
і  задані рівняннями
задані рівняннями 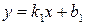 і
і  (рис. 3.5).
(рис. 3.5). кут нахилу прямої
кут нахилу прямої 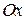 , а через
, а через  кут, на який потрібно повернути пряму
кут, на який потрібно повернути пряму 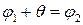 .
. і, якщо прямі не є перпендикулярними, то
і, якщо прямі не є перпендикулярними, то .
. і
і 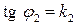 , отримаємо:
, отримаємо: . (8)
. (8) прямої з кутовим коефіцієнтом
прямої з кутовим коефіцієнтом 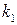 , до суміщення її з прямою, що має кутовий коефіцієнт
, до суміщення її з прямою, що має кутовий коефіцієнт 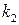 .
.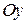 , то формула (8) не має змісту. В цьому випадку
, то формула (8) не має змісту. В цьому випадку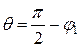 ,
,