 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Визначники квадратних матриць. Визначники 2- го і 3- го порядку
Необхідність введення визначника – числа, що характеризує квадратну матрицю Визначником матриці першого порядку
Наприклад, нехай Нехай задана система двох лінійних рівнянь із двома невідомими:
коефіцієнти якої складають квадратну матрицю другого порядку
Застосовуючи до системи (1) метод порівнювання коефіцієнтів, отримаємо:
Припустимо, що
Легко перевірити, підставляючи отримані значення невідомих у рівняння (1), що (3) є розв’язком (1). Спільний знаменник значень невідомих (3) дуже просто виражається через елементи матриці (2): він дорівнює добутку елементів головної діагоналі мінус добуток елементів другої діагоналі. Це число називається визначником (або детермінантом) матриці (2), ще кажуть, визначником другого порядку, тому що матриця (2) є матриця другого порядку. Для позначення визначника матриці (2) вживається наступний символ:
"+" "–"
Добутки Отже, визначником матриці другого порядку
Нехай дана система трьох лінійних рівнянь із трьома невідомими:
з матрицею із коефіцієнтів
Якщо помножити обидві частини першого рівняння системи (5) на число
Коефіцієнт при
Хоча вираз визначника третього порядку є досить громіздким, закон його складання з елементів матриці (6) виявляється досить простим. Справді, один із трьох членів визначника, що входять у його вираз (8) зі знаком плюс, буде добутком елементів головної діагоналі, кожний із двох інших – добутком елементів, що лежать на паралелі до цієї діагоналі з добавкою третього множника з протилежного кута матриці. Члени, що входять у (8) зі знаком мінус, будуються в такий же спосіб, але щодо другої діагоналі. Одержимо спосіб обчислення визначника третього порядку: "+" "–"
Ліворуч схематично показане обчислення додатних членів визначника третього порядку, праворуч – правило обчислення його від’ємних членів. Таким чином, одержимо спосіб обчислення визначника третього порядку (формула (8)), що зветься способом трикутника. Приведемо ще два способи розкриття визначників третього порядку. Другий спосіб розкриття визначника третього порядку називається способом Саррюса.
У цьому випадку до визначника дописуються перший і другий стовпці, і додатними членами визначника є добутки, що стоять на головній діагоналі і паралельно їй. Від’ємними елементами є елементи, що стоять на допоміжній діагоналі і паралельно їй.
Третій спосіб обчислення визначника третього порядку – це спосіб розкриття визначника третього порядку по елементах будь-якого рядка або будь-якого стовпця, ще його називають методом алгебраїчних доповнень. Розкриємо визначник по елементах першого рядка:
Дамо означення визначника Визначником квадратної матриці
Поиск по сайту: |
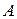 , – тісно зв’язана з розв’язанням систем лінійних рівнянь. Визначник матриці
, – тісно зв’язана з розв’язанням систем лінійних рівнянь. Визначник матриці  або
або  .
. або визначником першого порядку, називається елемент
або визначником першого порядку, називається елемент 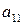 :
: .
. , тоді
, тоді  .
. (1)
(1) . (2)
. (2) .
. , тоді
, тоді ;
;  . (3)
. (3)



 і
і  називаються членами визначника другого порядку.
називаються членами визначника другого порядку. або визначником другого порядку називається число, що обчислюється за формулою (4).
або визначником другого порядку називається число, що обчислюється за формулою (4). (5)
(5) . (6)
. (6)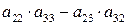 , обидві частини другого рівняння (5) на
, обидві частини другого рівняння (5) на 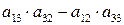 й обидві частин третього рівняння (5) на
й обидві частин третього рівняння (5) на  , а потім скласти всі три рівняння, то, коефіцієнти при
, а потім скласти всі три рівняння, то, коефіцієнти при 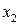 і
і  виявляться рівними нулю, тобто ці невідомі одночасно виключаються, і ми одержимо рівність:
виявляться рівними нулю, тобто ці невідомі одночасно виключаються, і ми одержимо рівність: (7)
(7) в цій рівності називається визначником третього порядку, який відповідає матриці (6).
в цій рівності називається визначником третього порядку, який відповідає матриці (6). (8)
(8)

 .
.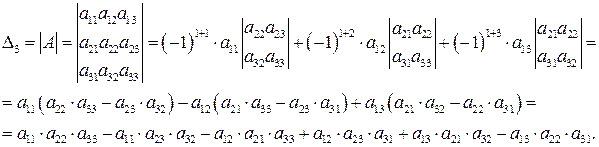
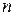 - ого порядку.
- ого порядку.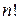 членів, кожний з яких є добутком
членів, кожний з яких є добутком