 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Матриці. Основні поняття. Види матриць
Однією з найважливіших задач математики є дослідження і розв’язання систем рівнянь першого степеня. Нехай система містить
Матрицею розміру Матриці позначаються прописними (заголовними) буквами латинського алфавіту: Наприклад, матриця
або в скороченому запису: Наприклад,
Поряд з круглими дужками використовуються і інші позначення матриці:
Дві матриці Матриця
яка містить і стовпець з вільних членів системи, називають розширеною матрицею системи. Види матриць Матриця, що складається з одного рядка – називається матрицею-рядком (вектор-рядком), а з одного стовпця – матрицею-стовпцем (вектор-стовпцем). Наприклад,
Матриця називається квадратною
Число рядків, (а отже і число стовпців) квадратної матриці називаєтьсяпорядком матриці. Елементи матриці Для квадратної матриці головну діагональ утворюють елементи Якщо всі недіагональні елементи квадратної матриці дорівнюють нулю, то матриця називається діагональною. Наприклад,
Якщо в діагоналі матриці
Матриця будь-якого розміру називається нульовою або нуль-матрицею, якщо всі елементи дорівнюють нулю:
Дії над матрицями Над матрицями, як і над числами, можна робити ряд операцій, причому деякі з них аналогічні операціям над числами, а деякі – специфічні.
1) Множення матриці на число Добутком матриці Наприклад, якщо Наслідок. Загальний множник всіх елементів матриці можна виносити за знак матриці. Наприклад,
В окремому випадку, добуток матриці
2) Додавання матриць Сумою двох матриць Наприклад,
3)Віднімання матриць Різниця двох матриць однакового розміру визначається через попередні операції:
4) Множення матриць Множення матриці Тоді добутком матриці
де Приклад. Обчислити добуток матриць Розв’язання. а) Знайдемо розмір матриці-добутку (якщо добуток матриць можливий):
б) Обчислимо елементи матриці-добутку
Багато властивостей, які належать до операцій над числами, справедливі і для операцій над матрицями (що випливає з означення цих операцій).
1. 2. 3. 4. 5. 6. 7.
Однак є і специфічні властивості матриць. Так, операція множення матриць має деякі відмінності від множення чисел: а) Якщо добуток матриць б) Якщо навіть добутки
Приклад. Знайти добуток матриць Розв’язання.
в) У випадку, якщо обидва добутки В окремому випадку комутативним законом володіє добуток будь-якої квадратної матриці
Таким чином, одинична матриця відіграє при множенні матриць ту ж роль, що й число г) Добуток двох ненульових матриць може дорівнювати нульовій матриці, тобто, з того, що
Наприклад,
5). Піднесення до степеня Цілим додатним степенем
Операція піднесення до степеня визначається тільки для квадратних матриць. За означенням маємо Приклад. Знайти Розв’язання. Варто відмітити, що з рівності
6). Транспонування матриці Транспонуванням матриці називається перехід від матриці
З означення випливає, що якщо матриця
Властивості операції транспортування: 1. 2. 3. 4.
Визначники
Поиск по сайту: |
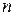 невідомих
невідомих  , що зв’язують
, що зв’язують 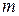 рівнянь
рівнянь  - го степеня (число рівнянь може не співпадати з числом невідомих). В загальному вигляді цю систему можна записати так:
- го степеня (число рівнянь може не співпадати з числом невідомих). В загальному вигляді цю систему можна записати так:
 називається прямокутна таблиця чисел, яка має
називається прямокутна таблиця чисел, яка має  ,..., а для позначення елементів матриці використовуються малі (рядкові) літери з подвійною індексацією:
,..., а для позначення елементів матриці використовуються малі (рядкові) літери з подвійною індексацією: 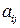 , де
, де 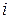 – номер рядка,
– номер рядка, 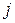 – номер стовпця.
– номер стовпця. (1)
(1) ,
,  ;
; 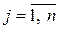 .
. .
. ,
,  .
.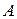 й
й 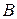 одного розміру називаються рівними, якщо вони співпадають почленно тобто:
одного розміру називаються рівними, якщо вони співпадають почленно тобто:  для
для 
 , (2)
, (2)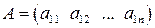 – матриця-рядок;
– матриця-рядок; – матриця-стовпець.
– матриця-стовпець. – квадратна матриця третього порядку.
– квадратна матриця третього порядку. , називаються діагональними й утворюють головну діагональ матриці.
, називаються діагональними й утворюють головну діагональ матриці. .
. – діагональна матриця третього порядку.
– діагональна матриця третього порядку. .
. – одинична матриця третього порядку.
– одинична матриця третього порядку.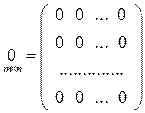 .
. (лямбда) називається матриця
(лямбда) називається матриця  , елементи якої
, елементи якої  , для
, для  ;
;  .
. , то
, то 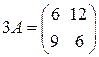 .
. .
. є нульова матриця, тобто
є нульова матриця, тобто  .
. , елементи якої
, елементи якої 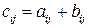 , для
, для  ,
,  , тоді
, тоді  .
. .
. називається така матриця
називається така матриця  , кожен елемент якої
, кожен елемент якої  , дорівнює сумі добутків елементів
, дорівнює сумі добутків елементів 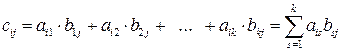 ,
, , де
, де 
 .
. ;
;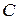 , помноживши елементи кожного рядка матриці
, помноживши елементи кожного рядка матриці  .
. ;
;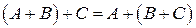 ;
; ;
; ;
;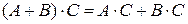 ;
; ;
; .
. існує, то після перестановки співмножників місцями добуток матриць
існує, то після перестановки співмножників місцями добуток матриць  може і не існувати. Дійсно, в останньому розглянутому прикладі отримали добуток матриць
може і не існувати. Дійсно, в останньому розглянутому прикладі отримали добуток матриць  , а ось добуток
, а ось добуток  не існує, оскільки число стовпців першої матриці не співпадає з числом рядків другої матриці.
не існує, оскільки число стовпців першої матриці не співпадає з числом рядків другої матриці.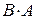 , якщо
, якщо  ,
,  .
. ;
;  , отже,
, отже, 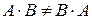 .
.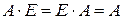 .
. не випливає, що матриця
не випливає, що матриця  , або матриця
, або матриця 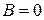 .
.
 , але
, але  .
.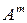
 квадратної матриці
квадратної матриці  .
.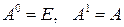 . Неважко показати, що
. Неважко показати, що  ,
,  .
. , де
, де  .
. .
. , ще не випливає, що
, ще не випливає, що 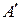
 , у якій рядки і стовпці помінялися місцями зі збереженням порядку.
, у якій рядки і стовпці помінялися місцями зі збереженням порядку.

 .
. ;
; ;
; ;
; .
.