Рецензенти: Тіман М.П., д-р фіз.-мат. наук, проф.
(Дніпропетровськ, ДАУ, зав. кафедри вищої математики)
Міхлін Ю.В., д-р фіз.-мат. наук, проф.
Конет І.М., д-р фіз.-мат. наук, проф.
(Кам’янець-Подільський, КПНУ ім. І. Огієнка, каф. диференціальних рівнянь і прикладної математики)
Р 82 Вища математика: навч. посіб.: у 2-х ч., ч 1. / М.О. Рубцов, В.І. Кравець, О.П. Назарова – Мелітополь: ТДАТУ, 2012. – 186 с.
Першу частину посібника написано відповідно до діючих програм курсу вищої математики для студентів всіх спеціальностей вищого навчального закладу. Посібник містить матеріал з лінійної алгебри, аналітичної геометрії та математичного аналізу. Теоретичний матеріал подано з великою кількістю розв’язаних прикладів, рисунків, завдань для самостійної роботи та контрольних питань і тестів для кожної теми, які перевіряють засвоєння матеріалу.
Цей посібник призначений для студентів технічних та економічних спеціальностей вищих навчальних закладів та заочного навчання.
| Вступ
|
|
| Розділ 1. ЕЛЕМЕНТИ ЛІНІЙНОЇ АЛГЕБРИ
|
|
|
| 1.1.
| Матриці
|
|
|
| 1.1.1.
| Матриці. Основні поняття. Види матриць
|
|
|
| 1.1.2.
| Дії над матрицями
|
|
|
| 1.2.
| Визначники
|
|
|
| 1.2.1.
| Визначники квадратних матриць. Визначники 2-го і 3-го порядку
|
|
|
| 1.2.2.
| Мінори та алгебраїчні доповнення
|
|
|
| 1.2.3.
| Властивості визначників
|
|
|
| 1.3.
| Особливі і неособливі матриці
|
|
|
| 1.3.1.
| Особливі і не особливі матриці. Обернена матриця
|
|
|
| 1.3.2.
| Ранг матриці. Властивості рангу
|
|
|
| 1.4.
| Елементарні перетворення матриці. Обчислення рангу матриці
|
|
|
| 1.4.1.
| Елементарні перетворення матриці. Обчислення рангу матриці
|
|
|
| 1.5.
| Системи лінійних рівнянь. Матричний метод розв’язання систем лінійних алгебраїчних рівнянь і формули Крамера
|
|
|
| 1.5.1.
| Системи лінійних рівнянь. Основні поняття і означення.
|
|
|
| 1.5.2.
| Система 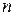 лінійних рівнянь з лінійних рівнянь з 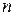 змінними. Метод оберненої матриці і формули Крамера змінними. Метод оберненої матриці і формули Крамера
|
|
|
| 1.6.
| Метод Гаусса
|
|
|
| 1.6.1.
| Метод Гаусса
|
|
|
| 1.7.
| Система 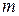 лінійних рівнянь з лінійних рівнянь з 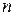 невідомими. Умови сумісності і несумісності лінійних систем. Теорема Кронекера-Капеллі невідомими. Умови сумісності і несумісності лінійних систем. Теорема Кронекера-Капеллі
|
|
|
| 1.7.1.
| Система 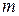 лінійних рівнянь з лінійних рівнянь з 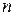 невідомими. невідомими.
|
|
|
| 1.7.2.
| Умови сумісності і несумісності лінійних систем. Теорема Кронекера-Капеллі
|
|
|
| 1.8.
| Однорідні системи лінійних рівнянь. Теорема про наявність ненульового розв’язку
|
|
|
| 1.8.1.
| Однорідні системи лінійних рівнянь. Теорема про наявність ненульового розв’язку однорідної системи
|
|
|
| 1.8.2.
| Знаходження лінійно-незалежних розв’язків, через які виражається всі інші
|
|
|
| 1.8.3.
| Зв’язок між розв’язками однорідних і неоднорідних систем рівнянь
|
|
|
|
| Питання до самоконтролю
|
|
|
|
| Тести до розділу 1
|
|
| Розділ 2. ЕЛЕМЕНТИ ВЕКТОРНОЇ АЛГЕБРИ
|
|
|
| 2.1.
| Вектори. Лінійні операції над векторами. Розклад вектора по ортонормованому базису
|
|
|
| 2.1.1.
| Скалярні і векторні величини. Лінійні операції над векторами: складання і віднімання векторів, множення вектора на число. Проекція вектора на вісь
|
|
|
| 2.1.2.
| Лінійна залежність і незалежність векторів, базис. Розкладання вектора по ортонормованому базису. Напрямні косинуси. Довжина вектора
|
|
|
| 2.2.
| Лінійні дії з векторами в координатній формі. Скалярний добуток векторів
|
|
|
| 2.2.1.
| Лінійні дії з векторами, заданими розкладом в ортонормованому базисі. Умови колінеарності векторів
|
|
|
| 2.2.2.
| Скалярний добуток векторів, його означення, фізичний зміст, властивості
|
|
|
| 2.2.3.
| Скалярний добуток векторів в координатній формі. Умови перпендикулярності двох векторів. Кут між векторами
|
|
|
| 2.3.
| Векторний і мішаний добутки векторів
|
|
|
| 2.3.1.
| Векторний добуток векторів, його означення, механічний зміст, властивості
|
|
|
| 2.3.2.
| Векторний добуток векторів в координатній формі
|
|
|
| 2.3.3.
| Мішаний добуток векторів, його геометричний зміст, властивості
|
|
|
| 2.3.4.
| Мішаний добуток векторів в координатній формі. Умова компланарності векторів
|
|
|
|
| Питання до самоконтролю
|
|
|
|
| Тести до розділу 2
|
|
| Розділ 3. ЕЛЕМЕНТИ АНАЛІТИЧНОЇ ГЕОМЕТРІЇ
|
|
|
| 3.1.
| Пряма лінія на площині
|
|
|
| 3.1.1.
| Поняття про рівняння лінії. Загальне рівняння прямої на площині і його дослідження
|
|
|
| 3.1.2.
| Рівняння прямої з кутовим коефіцієнтом. Рівняння прямої, що проходить через дану точку в заданім напрямку. Жмуток прямих
|
|
|
| 3.1.3.
| Рівняння прямої, що проходить через дві точки. Рівняння прямої у відрізках
|
|
|
| 3.1.4.
| Кут між двома прямими
|
|
|
| 3.1.5.
| Умови паралельності і перпендикулярності двох прямих
|
|
|
| 3.1.6.
| Відстань від точки до прямої
|
|
|
| 3.2.
| Площина. Пряма в просторі. Взаємне розміщення прямої і площини в просторі
|
|
|
| 3.2.1.
| Рівняння площини у векторній формі. Нормальне рівняння площини. Загальне рівняння площини і його дослідження
|
|
|
| 3.2.2.
| Рівняння площини, що проходить через одну і три точки
|
|
|
| 3.2.3.
| Кут між площинами. Умови паралельності і перпендикулярності двох площин
|
|
|
| 3.2.4.
| Параметричні рівняння прямої лінії в просторі. Канонічне рівняння прямої лінії в просторі. Рівняння прямої лінії в просторі, що проходить через дві задані точки
|
|
|
| 3.2.5.
| Кут між двома прямими в просторі. Умови паралельності і перпендикулярності двох прямих у просторі
|
|
|
| 3.2.6.
| Точка перетину прямої і площині. Кут між прямою і площиною. Умова паралельності і перпендикулярності прямої і площини
|
|
|
| 3.3.
| Лінії другого порядку
|
|
|
| 3.3.1.
| Коло
|
|
|
| 3.3.2.
| Еліпс
|
|
|
| 3.3.3.
| Гіпербола
|
|
|
| 3.3.4.
| Парабола
|
|
|
|
| Питання до самоконтролю
|
|
|
|
| Тести до розділу 3
|
|
| Розділ 4. ОСНОВИ МАТЕМАТИЧНОГО АНАЛІЗУ
|
|
|
| 4.1.
| Дійсні числа
|
|
|
| 4.1.1.
| Дійсні числа. Абсолютна величина (модуль) дійсного числа. Властивості абсолютних величин.
|
|
|
| 4.1.2.
| Сталі і змінні величини. Інтервали, 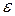 -окіл. -окіл.
|
|
|
| 4.2.
| Функція
|
|
|
| 4.2.1.
| Функція. Означення функції, область визначення, множина значень функції. Способи задання функції. Складна функція
|
|
|
| 4.2.2.
| Парність, непарність функції. Зростаючі і спадні функції. Обмежені функції. Періодичні функції
|
|
|
| 4.2.3.
| Класифікація функцій
|
|
|
| 4.2.4.
| Перетворення графіків
|
|
|
| 4.3.
| Границя змінної величини
|
|
|
| 4.3.1.
| Границя змінної величини. Геометрична інтерпретація границі. Єдиність границі
|
|
|
| 4.3.2.
| Нескінченно малі величини. Зв’язок змінної величини, що має границю з нескінченно малою величиною
|
|
|
| 4.4.
| Нескінченно великі величини. Правила граничного переходу
|
|
|
| 4.4.1.
| Нескінченно великі величини. Зв’язок між нескінченно малими і нескінченно великими величинами
|
|
|
| 4.4.2.
| Основні теореми про границю
|
|
|
| 4.4.3.
| Ознаки існування границі
|
|
|
| 4.4.4.
| Поняття про границю функції. Односторонні границі
|
|
|
| 4.5.
| Обчислення границь функцій
|
|
|
| 4.5.1.
| Перша чудова границя
|
|
|
| 4.5.2.
| Друга чудова границя. Число  , експонента. Натуральні логарифми, їх зв’язок з десятковими , експонента. Натуральні логарифми, їх зв’язок з десятковими
|
|
|
| 4.5.3.
| Еквівалентні нескінченно малі величини. Принцип відкидання нескінченно малих величин вищого порядку
|
|
|
| 4.6.
| Неперервність функції
|
|
|
| 4.6.1.
| Неперервність функції в точці. Умови неперервності
|
|
|
| 4.6.2.
| Класифікація точок розриву. Властивості функцій, неперервних на відрізку
|
|
|
|
| Питання до самоконтролю
|
|
|
|
| Тести до розділу 4
|
|
| Розділ 5. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЇ ОДНІЄЇ ЗМІННОЇ
|
|
|
| 5.1.
| Похідна
|
|
|
| 5.1.1.
| Похідна, її механічний, геометричний і аналітичний змісти
|
|
|
| 5.1.2.
| Диференціювання функцій і неперервність
|
|
|
| 5.1.3.
| Диференціювання суми, добутку, частки
|
|
|
| 5.1.4.
| Похідна складної функції
|
|
|
| 5.2.
| Похідні основних елементарних функцій
|
|
|
| 5.2.1.
| Похідна логарифмічної функції
|
|
|
| 5.2.2.
| Похідна степеневої функції. Логарифмічне диференціювання
|
|
|
| 5.2.3.
| Похідна показникової функції
|
|
|
| 5.2.4.
| Похідна степенево-показникової функції
|
|
|
| 5.2.5.
| Похідні від тригонометричних функцій
|
|
|
| 5.3.
| Похідна оберненої функції. Диференціювання гіперболічних функцій. Диференціювання функцій заданих неявно і параметрично. Похідні вищих порядків
|
|
|
| 5.3.1.
| Обернена функція і її диференціювання. Диференціювання обернених тригонометричних функцій
|
|
|
| 5.3.2.
| Гіперболічні функції, їх означення, графіки. Похідні гіперболічних функцій
|
|
|
| 5.3.3.
| Диференціювання неявних функцій
|
|
|
| 5.3.4.
| Диференціювання параметрично заданих функцій
|
|
|
| 5.3.5.
| Похідні вищих порядків
|
|
|
| 5.4.
| Диференціал
|
|
|
| 5.4.1.
| Диференціал функції
|
|
|
| 5.4.2.
| Геометричний зміст диференціала
|
|
|
| 5.4.3.
| Механічний зміст диференціала
|
|
|
| 5.4.4.
| Правила і формули обчислення диференціала
|
|
|
| 5.4.5.
| Диференціал складної функції. Інваріантність форми диференціала складної функції
|
|
|
| 5.4.6.
| Застосування диференціала до наближених обчислень
|
|
|
|
| Питання до самоконтролю
|
|
|
|
| Тести до розділу 5
|
|
| Розділ 6. ЗАСТОСУВАННЯ ПОХІДНОЇ
|
|
|
| 6.1.
| Основні теореми диференціального числення («Французькі» теореми)
|
|
|
| 6.1.1.
| Теорема Ролля і її геометричний зміст
|
|
|
| 6.1.2.
| Теорема Лагранжа і її геометричний зміст
|
|
|
| 6.1.3.
| Теорема Коші
|
|
|
| 6.2.
| Застосування диференціального числення до обчислення границь
|
|
|
| 6.2.1.
| Розкриття невизначеностей виду 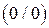 . Перша теорема Лопіталя-Бернуллі . Перша теорема Лопіталя-Бернуллі
|
|
|
| 6.2.2.
| Розкриття невизначеності виду  . Друга теорема Лопіталя-Бернуллі . Друга теорема Лопіталя-Бернуллі
|
|
|
| 6.2.3.
| Розкриття невизначеностей виду 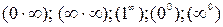 . .
|
|
|
| 6.3.
| Дослідження функцій
|
|
|
| 6.3.1.
| Необхідні і достатні умови зростання і спадання функції
|
|
|
| 6.3.2.
| Максимум і мінімум функції. Теорема Ферма. Необхідна умова існування екстремуму функції
|
|
|
| 6.4.
| Перша і друга достатні умови існування екстремуму
|
|
|
| 6.4.1.
| Дослідження функції на екстремум за допомогою першої похідної. Перша достатня ознака існування екстремуму. Алгоритм розрахунку
|
|
|
| 6.4.2.
| Дослідження функції на екстремум за допомогою другої похідної. Друга достатня ознака існування екстремуму. Алгоритм розрахунку
|
|
|
| 6.4.3.
| Знаходження найбільшого і найменшого значення функції на замкненому інтервалі. Алгоритм розрахунку
|
|
|
| 6.5.
| Опуклі функції
|
|
|
| 6.5.1.
| Опуклість і угнутість кривої. Точки перегину. Достатня ознака умови опуклості (угнутості). Інтервали опуклості (угнутості)
|
|
|
| 6.5.2.
| Достатня ознака існування точок перегину. Алгоритм знаходження інтервалів опуклості, угнутості і точок перегину
|
|
|
| 6.6.
| Загальний план дослідження функції і побудови графіків
|
|
|
| 6.6.1.
| Вертикальні, горизонтальні, похилі асимптоти кривої
|
|
|
| 6.6.2.
| Загальна схема дослідження функції і побудови графіка
|
|
|
|
| Питання до самоконтролю
|
|
|
|
| Тести до розділу 6
|
|
| Розділ 7. ФУНКЦІЇ БАГАТЬОХ ЗМІННИХ
|
|
|
| 7.1.
| Функції багатьох змінних. Основні поняття
|
|
|
| 7.1.1.
| Означення функції двох змінних. Область визначення. Приклади знаходження області визначення. Поверхні другого порядку
|
|
|
| 7.1.2.
| Неперервність функції двох змінних
|
|
|
| 7.1.3.
| Частинні похідні першого порядку
|
|
|
| 7.1.4.
| Повний диференціал
|
|
|
| 7.1.5.
| Частинні похідні вищих порядків
|
|
|
| 7.2.
| Похідна складної функції. Екстремум функції декількох змінних
|
|
|
| 7.2.1.
| Частинні похідні складних функцій та повний диференціал
|
|
|
| 7.2.2.
| Похідні неявних функцій двох змінних
|
|
|
| 7.2.3.
| Екстремум функції двох змінних. Необхідна умова існування екстремуму
|
|
|
| 7.2.4.
| Достатня умова існування екстремуму
|
|
|
| 7.2.5.
| Алгоритм знаходження екстремуму функції двох змінних
|
|
|
| 7.2.6.
| Алгоритм знаходження найбільшого і найменшого значення функції двох змінних в замкненій області
|
|
|
| 7.3.
| Елементи теорії поля
|
|
|
| 7.3.1.
| Скалярні і векторні поля
|
|
|
| 7.3.2.
| Похідна за напрямом
|
|
|
| 7.3.3.
| Градієнт скалярного поля і його властивості
|
|
|
| 7.3.4.
| Дивергенція та ротор
|
|
|
| 7.3.5.
| Потенціальне і соленоїдальне поля
|
|
|
| 7.4.
| Поняття про емпіричні формули. Метод найменших квадратів
|
|
|
| 7.4.1.
| Поняття про емпіричні формули
|
|
|
| 7.4.2.
| Метод найменших квадратів
|
|
|
|
| Питання до самоконтролю
|
|
|
|
| Тести до розділу 7
|
|
| Література
|
|
Цей посібник з курсу вищої математики для студентів всіх спеціальностей агротехнологічного університету створений з огляду на підвищення рівня фахової підготовки при безпосередньому застосуванні фундаментальної математичної підготовки, для покращення прикладної її спрямованості.
Актуальність математики в сучасних умовах визначається в технічних, агротехнологічних, гуманітарних дослідженнях. Для більшості галузей знань вона стала не лише інструментом кількісних розрахунків, а й методом точних умовиводів, засобом чіткого визначення понять і постановки проблем.
Навчальний посібник написано відповідно до діючих програм курсу вищої математики для студентів всіх спеціальностей вищого технічного наукового закладу.
Посібник ставить своєю метою допомогти студенту самостійно оволодіти теоретичною базою основних математичних понять, він дає змогу майбутнім фахівцям здобути ґрунтовну математичну освіту, що відповідає найвищим запитам сучасності. Це й визначило структуру посібника. Він складений на основі лекційного курсу, який формувався на протязі декількох останніх років на кафедрі вищої математики Таврійського Державного Агротехнологічного Університету. Навчальний посібник складається з двох частин. Запропонована до Вашої уваги перша частина містить сім розділів. Ці розділи охоплюють: елементи лінійної алгебри, елементи векторної алгебри, елементи аналітичної геометрії, основи математичного аналізу, диференціальне числення функції однієї змінної, застосування похідної та функції багатьох змінних. В кожному розділі після теоретичних відомостей приведені питання для самоконтролю та тестові завдання, що дозволить перевірити якість вивченого матеріалу.
Метою авторів було подати матеріал в доступній для студентів формі та заохотити їх до самостійного осмислення вивченого. Для більшої доступності та зрозумілості матеріалу широко використовувалася геометрична та фізична інтерпретація, розв’язки типових задач наводяться з короткими поясненнями теоретичних положень; надто складні чи громіздкі доведення, а також доведення, що ґрунтуються на поняттях які не входять в рамки програми, не приводяться. При написанні посібника були використані деякі матеріали та приклади, взяті з відомих навчальних посібників та задачників, які звичайно розглядаються на заняттях зі студентами.
Посібник призначається для студентів різних форм навчання вищих технічних закладів.
Автори висловлюють щиру подяку професорам, докторам наук Тіману М.П., Міхліну Ю.В., Конету І.М. за рецензування рукопису та зроблені зауваження.

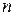 лінійних рівнянь з
лінійних рівнянь з 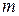 лінійних рівнянь з
лінійних рівнянь з 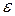 -окіл.
-окіл.
 , експонента. Натуральні логарифми, їх зв’язок з десятковими
, експонента. Натуральні логарифми, їх зв’язок з десятковими
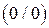 . Перша теорема Лопіталя-Бернуллі
. Перша теорема Лопіталя-Бернуллі
 . Друга теорема Лопіталя-Бернуллі
. Друга теорема Лопіталя-Бернуллі
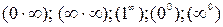 .
.