 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Отношения и соответствия. Функции как соответствия
Пусть А и В два множества. Тогда множество С={(a,b)|aЄA,bЄB} всех пар (a,b), где a и b независимо друг от друга принимают все значения соответственно из множеств А и В , называется декартовым произведением множеств А и В и обозначается АхВ. Если А и В – конечные множества, содержащие соответственно m и n элементов, то сразу видно, что множество АхВ содержит mn элементов. Самостоятельный интерес представляет частный случай, когда множества А и В совпадают: А=В. Чтобы его рассмотреть, введем новый термин. Упорядоченной парой элементов множества А будем называть объект (а1,а2), состоящий из двух (не обязательно различных) элементов а1,а2ЄA, с указанием, какой из них следует считать первым, а какой – вторым. Так, например, если А={1,2,3}, то упорядоченные пары (3,2) и (2,3) следует считать по определению различными. Упорядоченные пары будем заключать в круглые скобки и обозначать жирными строчными латинскими буквами а=(а1,а2) в отличие от неупорядоченных пар, которые как и множества элементов, записываются в фигурных скобках: {а1,а2} Назовем множество С={(а1,а2)| a1ЄA, а2ЄА} всех упорядоченных пар (а1,а2) элементов из А декартовым квадратом множества А и будем обозначать А2. Понятие упорядоченной пары можно обобщить на n элементов: упорядоченная n-ка элементов из А – это n (не обязательно различных) элементов множества А, данных в определенной последовательности a=(a1,a2,…,an). Упорядоченные n-ки элементов из множества А называют иногда кортежами над А. Определение декартова произведения двух множеств естественно обобщается на случай произвольного конечного числа множеств. Если А1,А2,…,Аn –n множеств, то под декартовым произведением понимается множество С = {(a1,a2,…,an)| a1ЄA1, а2ЄА2, …,anЄ Аn} всех последовательностей (a1,a2,…,an)= a, где i-ый член последовательности, называемый i-ой координатой последовательности а, принадлежит множеству Аi. Декартово произведение С обозначается через С= А1хА2х…хАn. В случае, когда все множества А1,А2,…,Аn совпадают, говорят об n-ой декартовой степени Аnмножества А, которая, очевидно, является множеством всех упорядоченных n-к из А. Самым важным для нас является случай, когда n=2. Всякое подмножество P декартова квадрата называется бинарным отношением на множестве А. На основе понятий соответствие и бинарное отношение в начале 20 века в математике было уточнено понятие функции. Функция f (отображение) — это закон или правило, согласно которому каждому элементу x из множества X ставится в соответствие единственный элемент y из множества Y. При этом говорят, что функция f задана на множестве X, или что f отображает X в Y. Если элементу Наличие функциональной зависимости между элементом
y = f(x), или В теоретической математике функцию f удобно определить как бинарное отношение (то есть множество упорядоченных пар Это и позволяет говорить о том, что элементу Таким образом, функция — это упорядоченная тройка (или кортеж) объектов (f,X,Y), где
Способы задания функции: · аналитический (в виде формулы); · табличный: · графический.
Поиск по сайту: |
 АхВ декартова произведения АхВ называется соответствием из А в В. Подмножество Р
АхВ декартова произведения АхВ называется соответствием из А в В. Подмножество Р 
 сопоставлен элемент
сопоставлен элемент  , то говорят, что элемент y находится в функциональной зависимости f от элемента x. При этом переменная x называется аргументом функции f или независимой переменной, множество X называется областью задания или областью определения функции, а элемент y, соответствующий конкретному элементу x — частным значением функции f в точке x. Множество Y всех возможных частных значений функции f называется её областью значений или областью изменения.
, то говорят, что элемент y находится в функциональной зависимости f от элемента x. При этом переменная x называется аргументом функции f или независимой переменной, множество X называется областью задания или областью определения функции, а элемент y, соответствующий конкретному элементу x — частным значением функции f в точке x. Множество Y всех возможных частных значений функции f называется её областью значений или областью изменения. или
или  ;
; ), которое удовлетворяет следующему условию: для любого
), которое удовлетворяет следующему условию: для любого 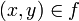 .
. или, что то же самое, график функции.
или, что то же самое, график функции.