 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Тема 3. Основы теории множеств и математической логики
3.1. Основные понятия теории множеств Понятие «множества» в математике и есть одно из самых простых, первоначальных и общих. Часто в повседневной жизни нам приходится говорить о нескольких вещах, объединенных некоторым общим признаком. Так, можно говорить о множестве предметов, находящихся на столе, множестве студентов, присутствующих в данный момент в аудитории, множестве звезд, наблюдаемых на небе, множестве всех точек, равноудаленных от данной, множестве всех клеток человеческого организма и т.д. Человеческому мышлению свойственно трактовать то или иное собрание предметов, родственных по какому-либо признаку, как самостоятельный объект. Совокупность кофейника, молочника, сахарницы, шести чашек и блюдец мы называем сервизом. Буквы А, Б, В, Г, Д, и т.д. объединяем в алфавит. Не случайно каждую из этих совокупностей мы называем существительным в единственном числе: сервиз, алфавит. Основное и самое существенное в понятии множества – это факт объединения различных объектов в одно целое. Основатель теории множеств немецкий математик и философ Георг Кантор писал: «Под многообразием или множеством я понимаю вообще всякое многое, которое можно мыслить как единое, т.е. всякую совокупность определенных элементов, которая может быть связана в одно целое с помощью некоторого закона». Перефразируя Кантора можно сказать, что множество— совокупность определенных, различимых между собой объектов, рассматриваемых как единое целое, и обладающая некоторым общим свойством. В приведенном определении можно выделить три важных признака, характеризующих понятие множества: 1) объекты, входящие во множество, определенные — т. е. для каждого объекта можно однозначно сказать, принадлежит ли он данному множеству или нет; 2) объекты, входящие во множество, различимы между собой — т. е. во множестве не может быть двух или более одинаковых объектов; 3) все объекты, входящие во множество, мыслятся как единое целое — т. е. во множестве абстрагируются от свойств отдельных объектов, но говорят об общем свойстве множества, как единого целого; такое общее свойство называют характеристическим. Например, можно говорить о множестве всех книг данной библиотеки, множестве всех вершин данного многоугольника, множестве всех натуральных чисел, множестве всех точек данной прямой. Множества обозначаются прописными буквами латинского алфавита: А, В, С, D ит. д. Объекты, входящие во множество, называют элементамии их обозначают строчными буквами. Книги данной библиотеки, вершины данного многоугольника, натуральные числа, точки данной прямой являются элементами соответствующих множеств. Множество, состоящее из конечного числа элементов, называется конечным,в противном случае множество называется бесконечным. Если множество содержит конечное число элементов, то оно может быть задано перечислением его элементов. Элементы множества выписываются подряд, разделяются запятыми, заключаются в фигурные скобки; порядок записи при этом роли не играет. Например, множество А, состоящее из трех букв а, б, в, может быть записано так: А = {а, б, в). Тот факт, что объект а является элементом множества А, записывается так: а Множество может содержать и всего лишь один элемент. Множество может быть задано при помощи правила, позволяющего определить, является ли данный объект элементом множества или нет. При записи правило, задающее множество, отделяется вертикальной чертой. Например, пусть множество В есть множество решений уравнения х2 - 5х + 6 = 0. Тогда можно записать так: В = {х Элементами множества В, корнями квадратного уравнения, являются числа 2 и 3, т.е. В = {2,3}. Может оказаться, что множество определено таким свойством, которым не обладает вообще ни один объект. Рассмотрим, например, множество треугольников, длины сторон которых равны 1 см, 2 см, 5 см. Из геометрии известно, что треугольника с такими длинами сторон не существует, т. е. так определенное множество не содержит ни одного элемента. Говорят, что эти множества пустые. Пустое множествоне содержит элементов, оно обозначается знаком Ø. Подмножество. Универсальное множество Множество В называется подмножествоммножества А, если каждый элемент множества В одновременно является элементом множества А. Это записывается так: В Пусть заданы множества А = {1,3,5,7} и В = {3,5}. Очевидно, что В есть подмножество А, т. е. В Множество N натуральных чисел является подмножеством множества Z целых чисел, т. е. N Если в множестве В найдется хотя бы один элемент, не принадлежащий множеству А, то В не является подмножеством множества А: В Из определения подмножества следует, что любое множество является подмножеством самого себя, т. е. справедливо утверждение Ас А. Говорят, что А — самое широкое подмножество А. Полагают также, что пустое множество является подмножеством любого множества. Это вполне естественно, так как пустое множество не содержит ни одного элемента и, следовательно, в нем нет элемента, который не принадлежал бы любому другому множеству. Пустое множество является самым узким подмножеством любого множества. Множество А и пустое множество Рассмотрим множество учеников некоторого класса; обозначим это множество X, и пусть У - множество учеников того же класса, получивших за контрольную по истории оценку «отлично». Если все ученики класса получили за эту контрольную отличную оценку, то Х и У равные множества: Х= У. Если же ни один ученик класса не получил «отлично», то множество У — пустое: У = 0. Но в любом случае множество У является подмножеством множества X: У
Пример 1. Пусть дано некоторое множество, состоящее из трех элементов а, b и с. Найти все его подмножества. Решение. Во-первых, это — пустое множество В-третьих, множества, содержащие по два элемента: {а, b}, {b, с}, {а, с}. И, наконец, само множество {а, b, с}. Число всех этих подмножеств равно восьми. Таким образом, любое множество, состоящее из трех элементов, имеет 8 = 23 подмножеств. Если конечное множество А состоит из n элементов, то число всех его подмножеств равно 2n. Из них ровно (2n-2) являются собственными подмножествами. Элементами множества могут выступать также и другие множества. В этом случае говорят не о множестве множеств, а о системе множеств. Например, взвод – это множество, состоящее из определенного числа солдат, рота – это множество, состоящее из нескольких взводов. Таким образом, рота – это множество, элементами которого являются множества (взводы). Частным случаем системы множеств является система всех подмножеств данного множества А. Так, система подмножеств множества А из задачи 1 имеет вид: Р(А)= Когда мы говорим о системе множеств, следует четко различать понятия «элемент множества» и «множество». Рассмотрим следующий пример. Студент Петров не может быть подмножеством множества студентов университета, поскольку он сам не множество, а элемент. Поэтому он, как элемент, может быть лишь элементом множества студентов университета. Студенческая же группа, как множество студентов, является подмножеством множества студентов университета. Предположим теперь, что некоторая группа состоит из одного студента, того самого Петрова. Получается, что сам студент Петров не может быть подмножеством, но группа, состоящая из него, может. Зафиксированное каким-либо образом множество объектов, допустимых при данном рассмотрении, называют базовым множеством, или основным множеством, или универсальным множеством. Например, для алгебры универсальным множеством является множество действительных чисел. Если мы рассматриваем множества точек на плоскости, то универсальным будет множество всех точек на плоскости.
Поиск по сайту: |
 А,ичитается «апринадлежит множеству А», или «а входит в множество А». Запись а
А,ичитается «апринадлежит множеству А», или «а входит в множество А». Запись а  А означает, что а не является элементом множества А.
А означает, что а не является элементом множества А. х2-5х + 6 = 0}.
х2-5х + 6 = 0}. А или А
А или А  В (обратите внимание на написание символа «подмножество»). В этом случае говорят, что множество В содержится в множестве А или множество А содержит множество В.
В (обратите внимание на написание символа «подмножество»). В этом случае говорят, что множество В содержится в множестве А или множество А содержит множество В.
 называются несобственными подмножествамимножества А. Все другие подмножества множества А называются собственными подмножествамимножества А.
называются несобственными подмножествамимножества А. Все другие подмножества множества А называются собственными подмножествамимножества А.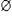 . Во-вторых, множества, содержащие по одному элементу: {а}, {b}, {с}.
. Во-вторых, множества, содержащие по одному элементу: {а}, {b}, {с}.
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 
 .
.