 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Основные законы математической логики
Коммутативность: А Ассоциативность: А Дистрибутивность: А А V(В Законы де Моргана:
Закон поглощения: А V(А Закон идемпотентности: А А А V«истина» = «истина», А V«ложь» = А. Закон противоречия: А Закон исключения третьего: А V Закон двойного отрицания: Вопросы для самопроверки: 1. Что называется множеством? 2.Назовите основные операции над множествами? 3.Что называется высказыванием? 4.Что понимают под простым, составным высказыванием? 5.Приведите примеры простых и составных высказываний. 6.Перечислите основные логические операции. Упражнения для самостоятельного выполнения: 1. Выпишите все подмножества множества В= 2. Пусть С=
3.Задайте перечислением следующие множества: 1) А= 3) С=
4. Найдите множества А 5. Заштрихуйте ту часть диаграммы, которая соответствует следующему множеству:
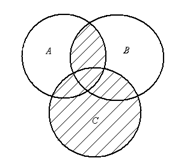
а) (АÈВ)\С; б) (АÇВ)È(СÇВ); в) (АÇВ) Ç (С \ В); г) (С\В)È(А\С); д) (А\С)È(ВÇС); е) (СÇА)\(ВÇА). 6. Запишите множество, изображенное с помощью кругов Эйлера на рисунке: а) б) в)
7. В двух группах учатся 50 курсантов. Для прибытия в институт 12 из них пользуются автобусом, 18 добираются пешком, 7 и идут, и едут в автобусе. Используя теорию множеств, найдите: 1) Сколько человек или добираются пешком или пользуются автобусом? 2) Сколько человек пользуются только автобусом? 3) Сколько человек пользуются другим транспортом?
8. Из 100 школьников 40 играют в футбол, а 50 - в волейбол. Каким может быть число школьников играющих а) в обе игры; б) хотя бы в одну игру?
9. Среди следующих высказываний укажите элементарные (простые) и составные (сложные). В составных высказываниях выделите грамматические связки: 1) число 27 не делится на 3; 2) число 15 делится на 5 и на 3; 3) если число 126 делится на 9, то оно делится на 3; 4) число 7 является делителем числа 42; 5) число 1269 делится на 9 тогда и только тогда, когда 18 делится на 9.
10. Обозначьте элементарные высказывания буквами и запишите следующие высказывания с помощью символов алгебры логики: 1) 45 кратно 3 и 42 кратно 3; 2) 45 кратно 3 и 12 не кратно 3; 3) если число 212 делится на 3 и 4, то оно делится 12; 4) число 212 - трехзначное и кратно 3 или 4.
11. Пусть А - истинное высказывание, В - ложное высказывание. Определите значение истинности следующих сложных высказываний: 1) (AÚ B)® A; 2) (A Ù B)® A; 3) A «(A Ù B) ® A; 4) A ® (B « A); 5) Тема 4. Структуры на множестве. Элементы комбинаторики
Область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов, называетсякомбинаторикой. В комбинаторных задачах необходимо подсчитать, сколькими способами можно сделать тот или иной выбор, выполнить то или иное требование, выполнить какое-либо условие. Первые комбинаторные задачи были связаны с азартными играми: картами, костями, «орлянкой». Наиболее любопытные игроки интересовались, например, тем, сколькими способами можно выбросить данное количество очков, бросая две или три кости или сколькими способами можно получить двух тузов при раздаче карт. Основы теоретических положений комбинаторики были разработаны французскими учеными Блезом Паскалем и Пьером Ферма в XVII веке. Дальнейшее развитие комбинаторика получила в работах Я. Бернулли, Г. Лейбница и Л. Эйлера. В наше время комбинаторика получила новый толчок для развития в связи с появлением быстродействующих ЭВМ и широким использованием методов дискретной математики. Комбинаторные методы используются для решения транспортных задач, задач по составлению расписаний, для разработки, кодирования и декодирования шифров, в задачах линейного программирования, статистики, теории информации. 4.1. Выборки и подмножества Пусть задано произвольное множество А из n объектов, состоящее из элементов аi. Последовательность произвольных элементов <а1,а2,...,ат >, аi называется выборкой объема т из А, или m-выборкой из множества А, или m-выборкой из n-множества А. Различие выборки и подмножества состоит в следующем. В выборке каждый элемент из некоторого множества А может встречаться произвольное число раз, т. е. объем выборки может превосходить объем исходного множества. Если же все компоненты m-выборки из n-множества A различны, то и m-выборка будет представлять собой т-подмножество множества А. Таким образом, выборка подразумевает возможность наличия в ней одинаковых элементов, а подмножество, как известно из определения множества, не допускает повторений элементов. Для отличия выборок от подмножеств в формулах для выборок вводят подчеркивание сверху (см. 4.1). Типичный пример выборки — слово в фиксированном алфавите, содержащее одинаковые буквы (например, слово «математика», составленное из букв русского алфавита). Упорядоченная и неупорядоченная выборки. Кратность элемента Если свойства выборки изменяются при транспозиции элементов (т. е. при перемене местами двух элементов), то выборка называется упорядоченной, в противном случае — неупорядоченной. Сравните, например, слова «волос» и «слово», составленные из букв русского алфавита. Упорядоченную выборку из множества десятичных цифр представляет собой телефонный номер, например, 5554433, так как номер 5454533 — это уже другой абонент. Число появлений в выборке одного и того же элемента аi называют его кратностью и обозначают
4.2. Размещения, перестановки, сочетания В комбинаторных задачах всегда необходимо подсчитать число всех подмножеств данного множества, удовлетворяющих определенным условиям, причем в одних задачах подмножества, отличающиеся порядком следования в них элементов, следует считать различными (случай размещений), в других порядок следования элементов неважен, и подмножества, отличающиеся только расположением элементов, не считаются различными (случай сочетаний). Рассмотрим размещения, перестановки, сочетания более подробно. Размещения Пусть имеется множество, состоящее из n элементов. Каждое его упорядоченное подмножество, содержащее k элементов, называется размещением из n элементов по k элементов. Из определения вытекает, что Размещения из n элементов по k элементов – все k-элементные подмножества n – элементного множества, различающиеся не только составом элементов, но и порядком их следования. Например, для четырехэлементного множества a, b, c, d размещениями из 4 элементов по 3 элемента являются подмножества: abc, acb, bac, bca, cab, cba, abd, adb, bad, bda, dab, dba, acd, adc, cad, cda, dac, dca, bcd, bdc, cbd, cdb, dbc, dcb. Число всех размещений из n по k элементов обозначается символом Число размещений из n по k элементов определяется следующей формулой: Запись n! читается «n-факториал» и представляет собой произведение всех натуральных чисел от 1 до n включительно: n! = 1 Условились считать, что 0! = 1! = 1. (4.3) 1!=1, 2!=1 Из приведенных выше вычислений факториала ряда чисел очевидно следующее равенство: n!=(n-1)! Тогда по формуле (4.2), учитывая (4.3) получаем
Кроме того, принимают Используя снова равенство n!=(n-k)!
Пример 1. В классе 30 учащихся. Сколькими способами могут быть выбраны староста и его заместитель, если каждый учащийся может быть избран на одну из этих должностей? Решение. Выбор Иванова старостой, Петрова — заместителем старосты, и выбор Петрова старостой, а Иванова — заместителем старосты — это два различных способа выбора, т. е. имеем случай упорядоченного подмножества: размещения из 30 элементов по 2. По формуле (4.2)
Пример 2. Сколько различных нарядов, состоящих из 7 курсантов, можно составить из взвода численностью 20 курсантов, если каждый курсант в наряде отличается от другого своими обязанностями? Решение. Количество различных нарядов равно числу размещений из 20 по 7 -
Пример 3.Сколько существует различных цифровых номеров автомашин, цифры которых не повторяются? Решение. Если цифры номера машины не повторяются, то количество комбинаций номеров равно числу размещений из 10 (общее количество цифр) по 3 (количество цифр в номере автомашины), т.е. равно
Число упорядоченных т-выборок из n-множества, т. е. размещений с повторениями, определяется по формуле Пример 4. Абонент забыл последние три цифры телефонного номера. Какое наибольшее число вариантов номеров ему нужно перебрать, чтобы дозвониться (в этом случае необходимый номер набирается последним)? Решение. Имеем случай размещения с повторениями из 10 элементов по 3. Действительно, цифра в любой из трех позиций может быть любая: 0, 1, 2, 3,4, 5, 6, 7, 8 или 9 (всего 10 вариантов), причем в соседних позициях могут присутствовать одинаковые цифры:
Перестановки Перестановками из n элементов называются размещения из n элементов по n элементов. Перестановки являются частным случаем размещения. Так как каждая перестановка содержит все n элементов множества, то различные перестановки различаются только порядком следования элементов. Число перестановок из n элементов обозначают символом Для того, чтобы вычислить число перестановок, подставим k=n в формулу (4.2) для нахождения размещений из n по n элементов: Значит, число перестановок из n элементов
Пример 5. Сколько существует вариантов проведения собрания учебной группы, если количество выступающих на собрании – 4? Решение. Так как на собрании должны выступить всего четверо ораторов, то число способов расположения их в списке выступающих и, соответственно, число способов проведения собрания равно числу перестановок из 4 элементов Пример 6.Сколько вариантов расположения слов допускает предложение: «Редактор вчера внимательно прочитал рукопись»? Решение. В данном предложении нет никаких грамматических ограничений на порядок слов, т. е. имеем случай перестановки из 5элементов по 5: P5 = 5! = 5 Пример 7.Для дежурства в классе в течение недели (кроме воскресенья) выделены 6учащихся. Сколькими способами можно установить очередность дежурств, если каждый учащийся дежурит один раз? Решение. В данной задаче рассматривается шестиэлементное множество дежурных и требуется определить число шестиэлементных подмножеств этого множества, отличающихся друг от друга только порядком следования элементов: P6 = 6! = 6 Число перестановок с повторениями определяется по формуле где п — число повторений в перестановке элементов i-го типа. Пример 8.Сколько различных перестановок можно образовать из букв слова «задача»? Решение. Поскольку в слове имеются 3буквы а, перестановки будут происходить с повторениями. Воспользуемся формулой для числа перестановок с повторениями, учитывая, что всего в слове 6букв, и каждая из букв з, д, ч встречается 1раз:
Сочетания
Если подмножества различаются не только составом элементов, но и порядком следования элементов, то они называются упорядоченными. Неупорядоченные подмножества различаются только составом входящих в них элементов. Так, у множества, состоящего из 5 элементов, имеется 10 неупорядоченных подмножеств, состоящих из 2 элементов и 20 упорядоченных. Пусть имеется множество, состоящее из n элементов. Каждое его неупорядоченное подмножество, содержащее k элементов, называется сочетанием из n элементов по k элементов. Из определения вытекает, что Сочетания из n элементов по k элементов – все k - элементные подмножества n – элементного множества, различающиеся только составом элементов. Подмножества, отличающиеся друг от друга порядком следования элементов, не считаются различными. Например, для четырехэлементного множество a, b, c, d сочетаниями из 4 элементов по 3 элемента являются подмножества: abc, abd, acd, bcd. Число всех сочетаний из n по k элементов обозначается специальным символом Число сочетаний из n по k элементов определяется следующей формулой:
Представив n! в виде n!=(n-k)! Если k=0, то Еще раз перепишем формулы (4.6), (4.2) и (4.5) в виде: Отсюда очевидно, что
Пример 9. Сколько различных нарядов, состоящих из 7 курсантов, можно составить из взвода численностью 20 курсантов? Решение. Количество различных нарядов равно числу сочетаний из 20 по 7 - Итак, количество различных нарядов равно 77520.
Пример 10. Сколько поединков по борьбе должны быть проведены между 15 спортсменами, если каждый из них должен встретиться с каждым. Решение. Должно состояться столько поединков, сколько существует двухэлементных подмножеств у множества, состоящего из 15 элементов, т.е. их число равно Итак, при встрече каждого из 15 спортсменов с каждым должно состояться 105 поединков. Пример 11. Читатель отобрал по каталогу 8 книг. Однако в библиотеке выдают одному читателю не более 5 книг. Сколько альтернатив взять книги есть у этого читателя? Решение. Читатель должен выбрать 5 книг из 8. Все книги разные и все равно, в каком порядке их взять. Имеем случай сочетания из 8 элементов по 5:
Пример 12. В турнире принимали участие 4 шахматиста, и каждые 2 шахматиста встретились 1 раз. Сколько партий было сыграно в турнире? Решение. Партий было сыграно столько, сколько можно выделить 2-элементных неупорядоченных подмножеств (так как каждые 2 шахматиста встречались только 1 раз, и поэтому сочетание Иванов - Петров и Петров-Иванов равнозначны) во множестве из 4 элементов, т. е.
Если пронумеровать игроков 1, 2, 3, 4, то это были партии 1-2, 3-4, 1-3, 2-4, 1-4, 2-3.
Число неупорядоченных т-выборок из n-множества, т. е. сочетаний с повторениями, определяется по формуле: Пример 13. Кости домино можно рассматривать, как сочетания с повторениями по 2 из 7 цифр: 0, 1,2, 3,4, 5, 6. Число всех таких сочетаний равно:
Число всех неупорядоченных подмножеств п-множества определяется по формуле: Nп=2n. Пример 14. В комнате 4 светильника. Сколько вариантов включения светильников может быть реализовано? Решение. Очевидно столько, сколько существует подмножеств у четырехэлементного множества, т. е. 24 = 16. При этом учитывается и тот способ «освещения», при котором ни один светильник не горит. Задачу можно также решить, рассматривая число всех двоичных цифр от 00002 до 11112, где 0 соответствует, например, выключенному светильнику, а 1 - включенному.
4.3. Основные правила комбинаторики Правило суммы для выбора 2 объектов.Если объект А можно выбрать n способами, а объект В – другими m способами, то выбор «или А, или В» можно осуществить n+m способами. При использовании правила суммы необходимо осознавать, что множество способов выбора объекта А и множество способов выбора объекта В не должно иметь общей части, в противном случае из суммы n+m нужно вычесть величину общей части множеств А и В. Пример 15. Преступник может проникнуть в квартиру либо через входную дверь, либо через окно. Число способов проникновения через дверь – 4, через окно – 3. Сколько всего существует способов проникновения в квартиру? Решение. Так как способы проникновения в квартиру через окно и через дверь различны, то мы можем воспользоваться правилом суммы. Тогда количество способов проникновения либо через окно, либо через дверь, т.е. количество различных способов проникновения в квартиру, будет равно 4+3=7.
Пример 16. От поселка Горелки до областной больницы г. Тулы можно доехать через Октябрьский поселок или центр города через Пролетарский мост. В первом случае можно воспользоваться автобусом № 1 или собственным автомобилем (количество вариантов равно 2), во втором — маршрутным такси № 2, маршрутным такси № 3 или воспользоваться собственным автомобилем (количество вариантов — 3). Сколькими способами можно добраться из поселка Горелки до областной больницы? Решение. Очевидно, что число разных вариантов проезда от поселка до больницы 2 + 3 = 5.
Пример 17. Пусть а — число, делящееся без остатка на 2, b — число, делящееся без остатка на 3. Сколькими способами можно выбрать «а или b» на множестве М = {1, 2, 3,4, 5}? Решение. 1)Числа, делящиеся без остатка на 2, — это числа 2 и 4, т. е. т = 2. 2) Без остатка на 3 из заданного множества М делится только число 3, т. е. п = 1. 3) Число искомых способов (т + п) = 2 + 1 =3.
Если способы выбора объекта типа а совпадают со способами выбора объекта типа b, то из формулы (т + п) следует вычесть число таких совпадений N2=(т + п- к), где к — число совпадений.
Пример 18. Пусть а — число, делящееся без остатка на 2, b — число, делящееся без остатка на 3. Сколькими способами можно выбрать «а или b» на множестве М = {1, 2, 3, 4, 5, 6} ? Решение. 1)Числа, делящиеся без остатка на 2, — это числа 2, 4 и 6, т. е. т = 3. 2) Числа, делящиеся без остатка на 3, — это числа 3 и 6, т. е. я = 2. 3) Число совпадений к =1, так как 6 попадает в первую и вторую выборку. Тогда число искомых способов (т + п — к) = =3+2-1=4
Правило суммы для выбора m объектов.Если объект
Правило произведения для выбора 2 объектов. Если объект А можно выбрать n способами и после этого действия объект В можно выбрать другими m способами, то выбор пары объектов (А, В) можно осуществить Действительно, каждый из n способов выбора объекта А можно скомбинировать с различными m способами выбора объекта В. А это и приводит к где Пример 19. Во взводе 25 курсантов. Сколько существует способов назначения командира взвода и его заместителя. Решение. Сначала выберем командира взвода. Число способов выбора равно 25, так как каждый курсант может быть назначен на эту должность. После этого остается 24 курсанта, из которых может быть назначен заместитель командира взвода. Т.е. число способов назначения заместителя командира – 24. По правилу произведения количество способов назначения пары курсантов на указанные должности Пример 20. В классе 30 учащихся. Сколькими способами могут быть выбраны староста и его заместитель, если каждый учащийся может быть избран на одну из этих должностей? Решение. Так как по условию задачи каждый учащийся может быть избран старостой, то, очевидно, существует 30 способов выбора старосты. Заместителем старосты может стать каждый из оставшихся 29 человек. Любой из 30 способов выбора старосты может осуществляться вместе с любым из 29 способов выбора заместителя старосты. Поэтому существует 30 Пример 21. Из Перми до Чайковского можно добраться теплоходом, поездом, автобусом или самолетом; из Чайковского до Ижевска — теплоходом или автобусом. Сколькими способами можно осуществить путешествие по маршруту Пермь — Чайковский — Ижевск? Решение. Число разных путей из Перми до Ижевска равно 4• 2 = 8, так как, выбрав любой из четырех возможных способов путешествия из Перми до Чайковского, имеем 2 возможных способа путешествия из Чайковского до Ижевска.
Правило произведения для выбора m объектов. Если объект Пример 22. Сколько существует целых четырехзначных чисел, не делящихся на 5 без остатка? Целое число не делится на 5, если оно не заканчивается на 5 или на 0. Решение. Первую значащую цифру можно выбирать девятью способами (все цифры, кроме нуля), вторую и третью - десятью способами, а четвертую лишь восемью (все цифры, кроме 0 и 5). Следовательно, целых четырехзначных чисел, не делящихся на 5 без остатка, существует: 9• 10• 10• 8 = 7200, где п1 =9, n2 = п3 = 10, n4 = 8 (см. правило произведения).
Пример 23. Для запирания некоторых автоматических камер хранения, кейсов применяют цифровые кодовые замки, которые отпираются при наборе заданной комбинации цифр. Замок состоит из 4 дисков, на каждом из которых нанесены все цифры. Сколько времени необходимо злоумышленнику для перебора всех комбинаций замка, если на одну комбинацию он тратит 2 секунды. Решение. При кодировании и открывании замка каждую цифру можно выбрать 10 способами. Всего цифр - 4, причем в комбинации важен порядок расположения цифр. Значит, по правилу произведения общее число комбинаций равно
Пример 24. Для дежурства в классе в течение недели (кроме воскресенья) выделены 6 учащихся. Сколькими способами можно установить очередность дежурств, если каждый учащийся дежурит один раз? Решение. В понедельник может дежурить любой из выделенных шести человек. Во вторник может дежурить каждый из еще не дежуривших пяти учащихся. Следовательно, расписание дежурств на первые два дня недели можно составить 6 • 5 способами. К среде остаются четыре человека, которые еще не дежурили, и поэтому на среду дежурного можно будет назначить 4 способами. Таким образом, существует 6•5•4 способов установления очередности дежурств на первую половину недели. В четверг сможет дежурить любой из трех еще не дежуривших учащихся, в пятницу — любой из двух еще не дежуривших. К субботе выбора не будет, так как останется один человек, который еще не дежурил. Он и будет дежурным в субботу. Ясно, что число способов, которыми можно установить очередность дежурств учащихся, равно 6• 5• 4• 3• 2• 1 = 720. Вопросы для самопроверки: 1) Чем отличаются размещения без повторений из n элементов по k от сочетаний без повторений из n элементов по k? 2) Что называется перестановками из n элементов? 3) Запишите формулы для вычисления размещений, сочетаний, перестановок без повторений (с повторениями). 4) В каком случае для выбора двух объектов используется правило суммы, а в каком правило произведения? Упражнения для самостоятельного выполнения: Правило суммы и произведения 1. В магазине имеется 6 сортов конфет и 4 сорта печенья. Сколько различных покупок, содержащих один сорт конфет и один сорт печенья, можно сделать в этом магазине? 2. На книжной полке стоят 10 книг по математике, 8 по физике, 3 по химии и 2 по литературе. Сколькими способами можно выбрать 4 книги так, чтобы они были разные? 3. Сколькими способами можно выбрать гласную и согласную буквы из слова «КАМЫШ»? Число векторов длины k над множеством А(n) 1. Сколько можно составить трехзначных чисел из цифр 1,2,3,4 и 5, если все цифры могут повторяться? 2. Сколько четырехзначных чисел можно составить из цифр 1 и 2? Общее число подмножеств множества А(n) 1. В некотором государстве нет жителей с одинаковым набором зубов. Какова может быть наибольшая численность населения государства? (Наибольшее число зубов принять равным 32) Размещения 1. В группе 20 человек. Необходимо избрать старосту, профорга и культорга. Сколькими способами можно образовать эту руководящую тройку, если одно лицо может занимать только один пост? 2. Сколькими способами можно составить флаг, состоящий из трех горизонтальных полос различных цветов, если имеется материал пяти различных цветов? Перестановки 1. Сколько различных слов, каждое из которых состоит из 7 букв, можно составить из слова «СОБЫТИЕ»? 2. Сколькими способами 4 человека могут разместиться в четырехместной каюте? 3. Сколько различных шестизначных чисел можно написать при помощи цифр 0,1,2,3,4,5? Цифры в числе не должны повторяться. Сочетания 1. Сколько различных стартовых шестерок можно образовать из числа 10 волейболистов? 2. В розыгрыше первенства по футболу приняло участие 10 команд. Каждая команда играла с каждой из остальных команд по одному раз. Сколько матчей было сыграно в розыгрыше? 3. Из колоды, содержащей 36 карт, вынули 10. - Сколькими различными способами это можно сделать? - В скольких случаях среди этих карт окажется хотя бы один туз? - В скольких случаях среди этих карт окажется ровно один туз? - В скольких случаях среди этих карт окажется 4 туза?
Поиск по сайту: |
 В = В
В = В  (А
(А  8, 12, 20
8, 12, 20 
 С,
С,
 С,
С,
 3
3  9}; 2) В=
9}; 2) В=  -2}.
-2}. В, А
В, А  С, А
С, А  В, В
В, В 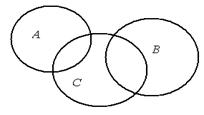



 г) д)
г) д)
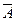 ®
®  .
. (4.1)
(4.1) (аi). Если каждый элемент аi m-выборки имеет кратность
(аi). Если каждый элемент аi m-выборки имеет кратность  .
. . (Читается: «число размещений из n по k» или «А из n по k»). А – первая буква французского слова «arrangement», что означает размещение, приведение в порядок.
. (Читается: «число размещений из n по k» или «А из n по k»). А – первая буква французского слова «arrangement», что означает размещение, приведение в порядок. . (4.2)
. (4.2) 2
2  .
. ,так как существует только одно подмножество n-множества, не содержащее элементов, - пустое множество.
,так как существует только одно подмножество n-множества, не содержащее элементов, - пустое множество. = 1, хотя
= 1, хотя  , где k>0. (4.4)
, где k>0. (4.4)
 . По формуле (4.4) вычисляем
. По формуле (4.4) вычисляем  = 390 700 800.
= 390 700 800. .
. ,m
,m  = 103 =1000.
= 103 =1000. . Р – первая буква французского слова «permutation» - «перестановка».
. Р – первая буква французского слова «permutation» - «перестановка». . (4.5)
. (4.5) . Т.е. множество из n элементов можно упорядочить n! способами.
. Т.е. множество из n элементов можно упорядочить n! способами. .
.  .
.
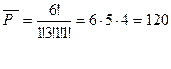
 . (Читается: «число сочетаний из n по k» или «С из n по k»). C – первая буква французского слова «combinasion» - «сочетание».
. (Читается: «число сочетаний из n по k» или «С из n по k»). C – первая буква французского слова «combinasion» - «сочетание». . (4.6)
. (4.6) (для k>0) (4.7)
(для k>0) (4.7)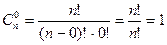 . Действительно, существует только одно пустое (не содержащее элементов) подмножество множества из n элементов.
. Действительно, существует только одно пустое (не содержащее элементов) подмножество множества из n элементов. .
. . Число размещений из n элементов по k элементов равно числу сочетаний из n элементов по k элементов, умноженному на число перестановок из k элементов.
. Число размещений из n элементов по k элементов равно числу сочетаний из n элементов по k элементов, умноженному на число перестановок из k элементов. . По формуле (4.7) получим
. По формуле (4.7) получим .
. . По формуле (4.7) получаем
. По формуле (4.7) получаем  .
.

 m
m 
 можно выбрать
можно выбрать  способами, объект
способами, объект  другими
другими  способами, объект
способами, объект  отличными от первых двух
отличными от первых двух  способами, и т.д., объект
способами, и т.д., объект  -
-  способами, отличными от первых (m-1), то выбор одного из объектов: или объекта
способами, отличными от первых (m-1), то выбор одного из объектов: или объекта 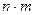 способами.
способами. ,
, , i=1, …, n способы выбора объекта А,
, i=1, …, n способы выбора объекта А,  , j=1, …, m способы выбора объекта B и выбор объекта В не зависит от выбора объекта А.
, j=1, …, m способы выбора объекта B и выбор объекта В не зависит от выбора объекта А. = 600.
= 600. 29 = 870 способов выбора старосты и его заместителя.
29 = 870 способов выбора старосты и его заместителя. . Таким образом, для перебора всех комбинаций необходимо потратить
. Таким образом, для перебора всех комбинаций необходимо потратить 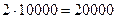 секунд или 5 часов 33 минуты и 20 секунд непрерывной работы. Заметим, что найденное время необходимо для перебора всех комбинаций. Но нужная комбинация может вовсе и не быть последней.
секунд или 5 часов 33 минуты и 20 секунд непрерывной работы. Заметим, что найденное время необходимо для перебора всех комбинаций. Но нужная комбинация может вовсе и не быть последней.