 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Тема 5. Случайные события и их вероятности
5.1. Основные понятия теории вероятностей В теории вероятностей событием А называют все то, что может произойти или не произойти при реализации некоторого комплекса условий С. Событие наступает в результате наблюдений или осуществления опытов (экспериментов). Примеры событий: А1 — выпадение нечетного числа очков при игре в кости; А2 — появление решки при бросании монеты; А3 — выход из строя компьютера после восьми часов работы; А4 — замерзание воды при отрицательной температуре; А5 — после января следует апрель. Все эти события отличаются в первую очередь тем, что возможность их появления различна. Одно событие (А4) происходит всегда, другое (А5) никогда не наступает, остальные могут произойти или не произойти в результате проведения одного опыта. Если при реализации условий С событие А всегда происходит, то оно называется достоверным (событие А4). Если же событие при заданных условиях никогда не наступает, то его называют невозможным (событие А5). Если в результате опыта при осуществлении определенного комплекса условий данное событие может наступить или не наступить, то оно называется случайным. Условия проведения такого опыта часто называют случайным опытом (экспериментом). Очевидно, что после бросания игральной кости нечетное число может выпасть, но оно может и не выпасть. Через восемь часов после включения компьютер может быть исправным, но может и выйти из строя. Элементарными называют события, не разложимые на более простые. Пусть при данных условиях проводится случайный опыт, в результате которого обязательно наступает одно и только одно из возможных элементарных событий. Множество Q всех элементарных событий wi. образует пространство элементарных событий, или полную группу событий. Например, при бросании игральной кости множество элементарных событий образует полную группу из шести элементарных событий wi (выпало одно очко, выпало два очка и т. д.): Q = { w1 =1, w2 =2, w3=3, w4 =4, w5 =5, w6 =6}. Наряду с элементарными рассматриваются так называемые составные, или разложимые события. Событие В называется составным, если можно указать, по меньшей мере, два таких элементарных события w1 и w2 что из существования каждого из них в отдельности следует существование события В. Этот факт записывается в виде: В = { w1, w2 }. Используя введенную ранее терминологию, случайным событием А называют любое подмножество S пространства элементарных событий (S Например, при бросании игральной кости составное событие А = {число очков четное} можно записать так: А = {2, 4, 6}, подразумевая при этом, что если выпадет число 2 или 4, или 6, то наступит событие А. Дополнение (противоположное к А) — это событие —А (читается «не А»), состоящее в ненаступлении события А. Пусть в урне 12 шаров, среди которых одна половина белых, а другая — черных. Тогда, если А — «вынуть белый шар», то —А — «вынуть не белый шар». События А1, А2, ... Аn называются несовместными, если в результате одного опыта никакие два из них не могут произойти одновременно. Это означает, что среди событий А1, А2, ... Аn нельзя найти такую пару событий Аj и Аi, в которой обнаружилось бы хотя бы по одному общему элементарному событию. Например, при однократном бросании игральной кости выпадение четного и нечетного числа — несовместные события. Несовместными являются также промах и попадание при одном выстреле по мишени. События А1, А2, ... Аn называются равновозможными, если нет оснований считать, что одно событие встречается чаще, чем другое. Например, выпадение орла или решки при бросании монеты. События А и В называются независимыми, если появление одного из них не изменяет шансы появления другого. Например, одновременно бросаются две игральные кости. Появление на одной из них трех очков никоим образом не зависит от того, какое количество очков появилось на верхней грани другой кости. Если появление одного события влияет на появление другого, то такие события называются зависимыми. Рассмотрим пример. В урне два красных и два черных шара. Вынимается один шар, записывается его цвет, и шар откладывается в сторону. Затем вынимается второй шар. Событие А — первый вынутый шар красный. Событие В — второй вынутый шар тоже красный. Очевидно, что эти события зависимы: если первым вынули красный шар, то шанс вынуть красный шар и во втором опыте будет меньше, чем если бы первым был вынут черный шар. Правила действий над событиями Объединением (суммой) событий А1, А2, ... Аn называется событие А, состоящее в наступлении хотя бы одного из этих событий: А = А1 Пример. В урне 6 шаров, которые отличаются только номером (1, 2, 3 и т. д.). Пусть событие Аi— «наугад выбрать шар под номером i». Тогда событие А = А1 + А3 + A5 состоит в том, что будет выбран шар с номером 1 или 3, или 5, т. е. с нечетным номером. Пересечением (произведением) событий А1, А2, ... Аn называется событие В, состоящее в обязательном наступлении всех этих событий: В = А1 Пример. В урне 12 шаров, среди которых одна половина белых с номерами от 1 до 6, а другая — черных с такими же номерами. Пусть событие А — «вынуть белый шар», событие В — «вынуть шар с нечетным номером». Тогда событие С= А Два события А и В, пересечение которых – невозможное событие, называются несовместимыми событиями. Два события А и В называются совместимыми, когда существует по крайней мере одно элементарное событие, благоприятствующее и событию А, и событию В. Рассмотрим пару событий: А – выпадение герба при подбрасывании монеты, В – невыпадение герба при подбрасывании монеты. Объединение этой пары событий – достоверное событие, пересечение этой пары событий – невозможное событие. Если объединение событий А и В – достоверное событие, а пересечение - невозможное событие, то события А и В называются противоположными. Это записывается таким образом: Аксиомы теории вероятностей Числовая функция Р(А) называется вероятностью события А, если она удовлетворяет следующим аксиомам. 1. Вероятность Р(А) есть неотрицательное число, заключенное между нулем и единицей: 0 < Р(А) < 1. 2. Вероятность достоверного события равна единице. 3. Вероятность невозможного события равна нулю.
5.2. Классическое определение вероятности Рассмотрим полную группу из п несовместных равновозможных событий. Примерами таких групп являются число очков при бросании игральных костей, число попаданий в мишень при выстрелах, проводимых в одинаковых условиях, появление шара с заданным номером при наличии в урне нескольких неразличимых на ощупь шаров. Пусть среди всех п возможных исходов опыта, только т исходов, образующих m-подмножество в полной группе, влекут за собой наступление события А. Случаи, входящие в т-подмножество, будем называть благоприятными. Например, в урне два белых, три черных и пять красных одинаковых на ощупь шаров. Будем считать благоприятным выбор белого шара; таких случаев два. Появление же черного или красного шара — случай неблагоприятный; таких случаев восемь. Вероятностью случайного события А называется отношение числа равновозможных элементарных событий, благоприятных событию А, к числу всех равновозможных элементарных событий определяемого данным испытанием: Р(А)= п — общее число всех элементарных равновозможных исходов опыта, 0 Алгоритм применения классической формулы для вычисления вероятностей при решении задач следующий: 1) удостовериться в том, что возможные исходы образуют множество несовместных равновозможных элементарных событий; 2) выбрать интересующее случайное событие А; 3) вычислить число возможных исходов (п) и число благоприятных исходов (т); 4) вычислить искомую вероятность Р (А).
Пример 1. Игральная кость бросается один раз. Какова вероятность выпадения четного числа очков? Решение. 1) Пусть событие А — выпадение четного числа очков. Таких исходов может быть три — числа 2, 4 или 6, т. е. т = 3. 2) Общее количество возможных исходов п = 6. 3) Получаем: Р(А) = Пример 2. Монета бросается один раз. Какова вероятность выпадения герба? Решение. Рассуждая по аналогии с предыдущей задачей, имеем: т = 1, п = 2, Искомая вероятность Р(А) = Пример 3. Монета бросается два раза. Какова вероятность: 1)выпадения орла хотя бы один раз (событие А); 2)двукратного выпадения орла (событие В)? Решение. 1)Равновозможными элементарными исходами здесь являются: ОО, ОР, РО, РР; число их. 2)Событию А благоприятствуют исходы ОО, ОР, РО, число которых т =3. Следовательно: Р(А) = 3) Событию В благоприятствует один исход ОО {т,=1). Поэтому: Р(В) = Пример 4. Опыт заключается в подбрасывании двух монет: медной и серебряной. Какова вероятность того, что хотя бы на одной монете выпадет орел? Решение. 1) Равновероятными элементарными исходами опыта являются следующие: w1— орел выпал на обеих монетах; w2 — орел выпал только на медной монете; w3 — орел выпал только на серебряной монете; w4 — орел не выпал ни на одной монете; т. е. п = 4. 2) Благоприятствуют событию А (появлению орла хотя бы 3) Получаем: Р(А) = Пример 5. В ящике лежат 20 одинаковых на ощупь шаров. Из них 12 белых и 8 черных. Наугад вынимают один шар. Какова вероятность того, что он окажется белым? (Точный смысл выражения «наугад вынимается шар» будет выяснен в процессе решения.) Решение. 1)В этой задаче рассматривается следующий опыт: из ящика наугад вынимают шар и смотрят его цвет. Сразу напрашивается множество исходов, состоящее из двух событий: Ч= «вынутый шар черный» и Б = «вынутый шар белый». Но эти исходы неравновероятны, так как белых шаров больше и шансов вынуть белый шар больше. 2)Для выявления в этом опыте множества равновероятных исходов внесем в опыт дополнительный элемент, не нарушающий вероятностной структуры задачи, а именно, перенумеруем все шары. Белым шарам поставим в соответствие номера с 1 по 12, а черным — номера с 13 по 20. 3)События Ак = «вынут шар с номером k» уже равновероятны, так как шары на ощупь неотличимы и вынимаются наугад. Кроме того, эти 20 событий образуют множество исходов нашего опыта. Следовательно, п = 20, а интересующему нас событию В = «вынутый шар белый» благоприятствуют первые 12 исходов, т. е. т = 12. Получаем: Р(В) = 4) Точный смысл выражения «наугад вынимается шар» состоит в том, что введенные события Ак равновероятны. При решении задач вычисления вероятностей часто оказываются полезными формулы комбинаторики(тема 4). Пример 6. Игральная кость бросается два раза. Какова вероятность того, что сумма выпавших очков равна 6 (событие А)? Решение. 1) Равновозможными элементарными исходами здесь являются пары (х, у), где х и у принимают значения 1,2, 3,4, 5 или 6. Общее число элементарных исходов п = 36 (см. правило произведения). 2) Событию А благоприятствуют пары (1, 5), (2, 4), (3, 3), (3, 3), (4, 2), (5, 1), число которых т = 5. 3) Получаем: Р(А) = Пример 7. Набирая номер телефона, абонент забыл две последние цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Какова вероятность того, что номер набран правильно? Решение. 1) Две последние цифры можно набрать числом способов, равным числу упорядоченных двухэлементных подмножеств у десятиэлементного множества (множества всех цифр). Это число способов равно А102 2) Благоприятствует событию А (цифры набраны верно) только один исход (т = 1). 3) Получаем: Р(А) = Пример 8. Среди 40 электроламп 5 испорченных. Какова вероятность того, что выбранные наудачу 3 лампы окажутся исправными? Решение. 1) Выбор трех ламп из 40 — это число сочетаний из 40 по 3 (С403), так как порядок выбора ламп не имеет значения. Лампы выбирают наудачу. Это означает, что все эти способы выбора (все исходы) равновероятны. Имеем число возможных исходов: n= 2) Число благоприятных исходов — это три лампы из 35 исправных, т. е. число сочетаний из 35 по 3: m= 3) Искомая вероятность Р(А) = Пример 9. Из пяти букв разрезной азбуки составлено слово «книга». Неграмотный мальчик перемешал буквы и потом наугад их собрал. Какова вероятность того, что он опять собрал слово «книга»? Решение. 1) Введем обозначение: событие А — собрано слово «книга». 2) В этом опыте элементарными событиями будут все возможные перестановки из пяти различных букв к, н, и, г, а. Число таких перестановок: Р5 =5!=120 = п . 3) Только в одном из этих случаев будет составлено слово «книга», т. е. т = 1. 4) Получаем: Р(А) = Пример 10. На полке стоят 6 одинаковых банок: 3 с зеленой краской и 3 — с красной. Наугад берут три банки. Какова вероятность того, что эти банки содержат краску одного цвета?
Решение. 1) Составим вероятностную модель данного опыта. Будем считать, что банки занумерованы числами 1, 2, 3, 4, 5, 6, при этом первые три содержат зеленую краску, а последние три — красную. Тогда естественно считать, что элементарным исходом нашего опыта является тройка выбранных чисел, причем порядок чисел неважен. 2) Количество возможных исходов — это число сочетаний из 6 по 3, т. е. п = С36 = 20. 3) Благоприятных исходов два, а именно (1, 2, 3) и (4, 5, 6), т. е. т = 2. Пример 11. На складе имеется 15 кинескопов, причем 10 из них изготовлены заводом «Рубин». Найти вероятность того, что среди пяти наудачу взятых кинескопов окажутся 3 кинескопа завода «Рубин». Решение. 1) Элементарным исходом следует считать пятерку выбранных кинескопов. 2) Общее число исходов п = С155 = 3003. 3) Подсчитаем число благоприятных исходов. При благоприятных исходах среди выбранных кинескопов должны быть: q1-3 кинескопа завода «Рубин» и q2-2 кинескопа других заводов. То есть благоприятные исходы т — это произведение q1• q2, так как именно произведение соответствует логическому и (см. раздел, посвященный логическим операциям). 4)3 кинескопа завода «Рубин» из 10 можно выбрать С103 = 120 способами. 2 кинескопа других заводов выбираем из 15 - 10 = 5: число сочетаний — С52 =10. т = С103• С52 = 120 • 10 = 1200. 5) Искомая вероятность Р(А) = 5.2. Классическое и статистическое определение вероятности Классическое определение вероятности события предполагает, что: 1) число элементарных исходов конечно; 2) все эти исходы равновозможны. Однако на практике встречаются испытания с бесконечным числом различных возможных исходов. Кроме того, нет общих методов, позволяющих результат испытания, даже с конечным числом исходов, представить в виде суммы или объединения равновозможных элементарных исходов. Поэтому применение классического определения вероятности весьма ограниченно. Мы укажем сейчас другое определение вероятности, иногда более удобное для приложений. Рассмотрим пример. Пусть в урне 10 одинаковых по размеру шаров, из них два белых, три черных и пять красных. Случайный опыт заключается в том, что вынимается наугад один шар. При этом шар может оказаться белым или черным, или красным. Будем в каждом опыте вытаскивать шар, фиксировать его цвет, опускать вынутый шар обратно в урну и тщательно перемешивать там шары. В результате каждого проведенного опыта можно вытащить шар любого из трех возможных цветов: событие А1 — вынут белый шар, А2 — вынут черный шар, А3 — красный шар. Если проводить такой опыт значительное число раз (п — велико), то окажется, что примерно в половине случаев вынули красный шар, в двадцати процентах случаев — белый, а в тридцати — черный. По мере увеличения числа проведенных опытов уверенность в соотношении шансов возможных событий, соответственно 5:2:3, будет подтверждаться со все большей точностью. Частота появления каждого из возможных событий, или относительная частота события: P= где i = При числе испытаний п Р(Аi)=lim Пример 12. В результате ряда испытаний было обнаружено, что при 200 выстрелах стрелок попадает в цель в среднем 190 раз. Какова вероятность поражения цели стрелком? Сколько для него попаданий в цель можно ожидать при 1000 выстрелах? Решение. 1) Используя статистическое определение вероятности, имеем: Р=190/200≈0,9506 (95%). 2) Число удачных выстрелов из 1000 выстрелов примерно составляет 1000*0,9506=951
Поиск по сайту: |
 Q). Содержательно это означает, что появление любого из элементарных событий, входящих в S, влечет за собой появление события А.
Q). Содержательно это означает, что появление любого из элементарных событий, входящих в S, влечет за собой появление события А. А2
А2  А2
А2  А2
А2 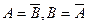 .
. , где т — число элементарных исходов, благоприятных событию А,
, где т — число элементарных исходов, благоприятных событию А, т
т 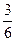 = 0,5.
= 0,5. = 0,5.
= 0,5. = 0,75.
= 0,75.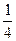 = 0,25.
= 0,25.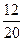 = 0,6.
= 0,6.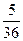 = 0,13(8).
= 0,13(8). (см. размещения). Следовательно, всего существует п =
(см. размещения). Следовательно, всего существует п = 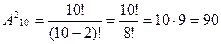 исходов.
исходов.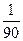 = 0,0(1).
= 0,0(1).
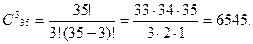
 = 0,662.
= 0,662.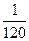 = 0,008(3).
= 0,008(3).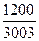 = 0,3996.
= 0,3996.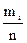
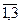 .
.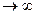 относительная частота события колеблется около некоторого постоянного числа Р, называемого статистической вероятностью:
относительная частота события колеблется около некоторого постоянного числа Р, называемого статистической вероятностью: