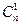|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Биномиальное распределение. Формула Бернулли
Формула Бернулли Пусть производится n независимых друг от друга испытаний, в каждом из которых случайное событие А может либо произойти, либо не произойти. Результат каждого испытания — случайное событие, вероятность которого естественно считать независящей от результатов других бросаний. Вероятность того, что событие А состоится в каждом испытании одна и та же и равна p. Следовательно, вероятность того, что событие А не произойдет, равна 1–р. Обозначим эту величину через q=1–р. Зададимся вопросом, какова будет вероятность того, что при n испытаниях событие А наступит в k из них и, соответственно, в n-k испытаниях не наступит? Для подсчета вероятности По теореме сложения вероятностей для несовместных событий вероятность наступления события А в k из n испытаниях Таким образом, Полученная формула носит название формулы Бернулли. Ясно, что несовместные сложные события, состоящие в появлении события А 0 раз, 1 раз, 2 раза, …, n раз в n испытаниях образуют полную группу событий. Поэтому сумма вероятностей этих событий Это соотношение можно получить, непосредственно вычислив сумму Пример 29.Построить ряд распределения числа выпавших гербов при двух бросках монеты. Случайная величина – количество выпавших гербов при двух подбрасываниях монеты, в отличие от примера 6.1, может принимать три значения: 0, 1 и 2. Значение Ряд распределения запишется в виде:
Пример 30.Стрелок производит три выстрела по мишени. Вероятность попадания при каждом выстреле равна 0,6. Построить ряд и многоугольник распределения числа попаданий в мишень. Случайная величина Х – число попаданий в мишень при трех выстрелах. Возможные значения Х: где вероятность попадания при одном выстреле p=0,6 , q - вероятность промаха, q=1–0,6=0,4.
Ряд распределения случайной величины Х имеет вид:
Можно проверить, что, действительно, Многоугольник распределения числа попаданий при трех выстрелах изображен на рис.5.3.
Рис. 5.3 Распределения случайных величин в примерах 6.3 и 6.4 являются частными случаями биномиального распределения вероятностей при n=2 и n=3. Биномиальнымназывается распределение вероятностей, определяемое формулой Бернулли: Формула (6.1) является аналитическим выражением биномиального закона распределения. По биномиальному закону распределена случайная величина Хчисла появлений события А при проведении n независимых испытаний, если вероятность появления события А в каждом испытании одинакова и равна p (q=1–p). В n испытаниях событие А может вообще не появиться, появиться 1 раз, 2 раза, 3 раза, …, n раз. Таким образом, возможные значения Х таковы:
Cумма вероятностей, соответствующих возможным значениям случайной величины, записывается в виде бинома Ньютона: Естественно, что в формуле (6.2) p+q=1 и поэтому
Поиск по сайту: |
 пронумеруем испытания. Для начала найдем вероятность наступления события А в испытаниях с определенными k номерами, и ненаступления в остальных n-k испытаниях. Так как испытания независимы, то по теореме умножения вероятностей получим вероятность такого сложного события равной
пронумеруем испытания. Для начала найдем вероятность наступления события А в испытаниях с определенными k номерами, и ненаступления в остальных n-k испытаниях. Так как испытания независимы, то по теореме умножения вероятностей получим вероятность такого сложного события равной 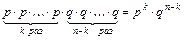 . Наше искомое событие, состоящее в наступлении А в любых k испытаниях из общего числа n испытаний, разбивается на вышеупомянутые сложные несовместные события, количество которых
. Наше искомое событие, состоящее в наступлении А в любых k испытаниях из общего числа n испытаний, разбивается на вышеупомянутые сложные несовместные события, количество которых  . Например, если n=4, а k=2, то такие события: AA
. Например, если n=4, а k=2, то такие события: AA 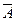
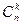
 (сумма
(сумма  ).
).
 для 0£ k£ n равна единице:
для 0£ k£ n равна единице: 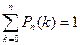 .
. ):
): =
= 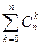
 =
= 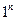 =1.
=1.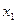 =0 соответствует тому, что герб не выпал ни разу, значение
=0 соответствует тому, что герб не выпал ни разу, значение  =1 соответствует выпадению герба и решки или решки и герба, значение
=1 соответствует выпадению герба и решки или решки и герба, значение  =2 – выпадению двух гербов. Соответствующие вероятности можно найти по формуле Бернулли, но еще легче по теоремам умножения и сложения вероятностей:
=2 – выпадению двух гербов. Соответствующие вероятности можно найти по формуле Бернулли, но еще легче по теоремам умножения и сложения вероятностей:  ;
;  ;
;  .
.  .
.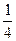

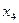 =3. Вероятность того, что произойдут k попаданий (k=0, 1, 2, 3) при трех выстрелах подсчитывается по формуле Бернулли (5.7):
=3. Вероятность того, что произойдут k попаданий (k=0, 1, 2, 3) при трех выстрелах подсчитывается по формуле Бернулли (5.7):

 (0£ k£ 3),
(0£ k£ 3),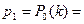

 =
= 
 =
= 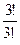
 =0,064;
=0,064;

 =
= 
 =
= 
 =3
=3 

 =
= 
 =
=  =3
=3 

 =
= 
 =
= 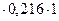 =0,216.
=0,216. =0,064+0,288+0,432+ +0,216=1.
=0,064+0,288+0,432+ +0,216=1.
 =n. А соответствующие им вероятности подсчитываются по формуле Бернулли (6.1). Ряд распределения в этом случае будет таким:
=n. А соответствующие им вероятности подсчитываются по формуле Бернулли (6.1). Ряд распределения в этом случае будет таким: