 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Геометрическое распределение
Пример 31. Стрелком производятся выстрелы по мишени до первого попадания. Вероятность попадания в каждом выстреле равна p=0,6. Построить ряд распределения количества произведенных выстрелов. Обозначим через Х дискретную случайную величину – число произведенных выстрелов до первого попадания. Возможными значениями Х являются натуральные числа Вероятность того, что случайная величина принимает значение Подсчитаем вероятность того, что случайная величина принимает значение Таким образом, ряд распределения случайной величины запишется так:
Многоугольник распределения случайной величины построен на рис.5.4 до значения
Рис. 5.4 Можно заметить, что ряд вероятностей, соответствующих значениям случайной величины, образует бесконечную убывающую геометрическую прогрессию со знаменателем q=0,4 и первым членом p=0,6: 0,6; 0,6×0,4; 0,6× Поэтому распределение случайной величины в примере (6.5) называют геометрическим. Геометрическимназывается распределение вероятностей случайной величины Х, которое определяется следующим законом: Здесь p – вероятность наступления события А, q - вероятность того, что событие А не произойдет: q=1–p. Случайная величина Х определяется как число независимых испытаний, которые нужно произвести до первого появления события А. Очевидно, что возможными значениями Х является множество натуральных чисел xÎN. То, что случайная величина принимает значение
Поиск по сайту: |
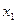 =1,
=1,  =2,
=2,  =3, …. Множество значений Х является бесконечным счетным множеством, как и ряд натуральных чисел.
=3, …. Множество значений Х является бесконечным счетным множеством, как и ряд натуральных чисел. =p=0,6. Вероятность принятия случайной величиной значения
=p=0,6. Вероятность принятия случайной величиной значения  =(1–p) ×p=(1–0,6)×0,6=0,4×0,6=0,24. Аналогичным образом находятся вероятность
=(1–p) ×p=(1–0,6)×0,6=0,4×0,6=0,24. Аналогичным образом находятся вероятность 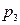 значения случайной величины
значения случайной величины 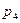 =
= 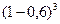 ×0,6=
×0,6= 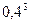 ×0,6=0,0384,
×0,6=0,0384,  =
=  ×0,6=
×0,6= 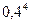 ×0,6=0,01536 и т.д.
×0,6=0,01536 и т.д.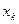 =k. Это означает, что попадание произошло лишь в k-м выстреле, а до этого был k-1 промах. Так как все выстрелы независимы друг от друга, то по теореме умножения вероятностей
=k. Это означает, что попадание произошло лишь в k-м выстреле, а до этого был k-1 промах. Так как все выстрелы независимы друг от друга, то по теореме умножения вероятностей 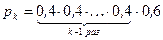 =
= 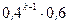 .
.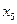 =5 (множество значений дискретной случайной величины – бесконечное)
=5 (множество значений дискретной случайной величины – бесконечное)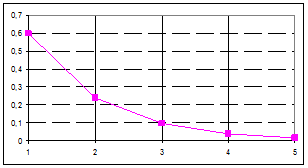
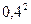 ; 0,6×
; 0,6× 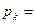
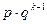 , k³1.
, k³1. =
= 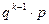 . Сумма вероятностей всех значений определяется по формуле суммы членов убывающей геометрической прогрессии со знаменателем q и первым членом p:
. Сумма вероятностей всех значений определяется по формуле суммы членов убывающей геометрической прогрессии со знаменателем q и первым членом p: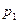 +
+  +…=
+…= 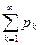 =
=  =
= 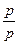 =1.
=1.