 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Числа, переменные величины, выражения. Числовые функции
Одним из основных понятий математики является понятие числа. Оно развивалось в тесной связи с изучением величин; эта связь сохраняется и теперь. Во всех разделах современной математики приходится рассматривать разные величины и пользоваться числами. Существует большое количество определений понятия «число». Первое научное определение числа дал Эвклид в своих «Началах»: «Единица есть то, в соответствии с чем каждая из существующих вещей называется одной. Число есть множество, сложенное из единиц». Еще раньше Эвклида Аристотель дал такое определение: «Число есть множество, которое измеряется с помощью единиц». Со слов греческого философа Ямвлиха, еще Фалес Милетский – родоначальник греческой стихийно-материалистической философии – учил, что «число есть система единиц». Это определение было известно и Пифагору. В своей «Общей арифметике» (1707 г) великий английский физик, механик, астроном и математик Исаак Ньютон пишет: «Под числом мы подразумеваем не столько множество единиц, сколько абстрактное отношение какой-нибудь величины к другой величине такого же рода, взятой за единицу. Число бывает трех видов: целое, дробное и иррациональное. Целое число есть то, что измеряется единицей; дробное – кратной частью единицы, иррациональное – число, не соизмеримое с единицей». В настоящее время в школьном курсе математики изучаются следующие числовые множества: 1. Положительные целые (натуральные) числа; 2. Положительные и отрицательные целые числа и нуль; 3. Рациональные числа, в которые дроби входят на равных правах с целыми числами; 4. Действительные числа, включая иррациональные числа, такие, как, например, число π Применение математики для решения практических задач, при решении которых необходимо было описывать движение тел и изменения, происходящие в процессах и объектах, было затруднено, пока она рассматривала только постоянные величины. Одним из первых задумался над такими задачами основатель динамики Галилео Галилей (1564-1642). Он размышлял над тем, как меняется скорость падающего тела, как движется точка на ободе колеса, как качается маятник. Решить такие задачи ему удалось лишь в простейших случаях. Чтобы создать математический аппарат для изучения движений, понадобилось понятие переменной величины. Это понятие было введено в математику в 17 веке французским философом и математиком Рене Декартом (1596-1650). Этим термином обозначались различные меняющиеся величины. При записи зависимостей между величинами Декарт стал применять буквы. При этом операции над величинами соответствовали операции над буквами. Отношения между известными и неизвестными величинами Декарт выражал в виде уравнений. Из чисел и переменных составляются выражения. Одним из основных видов выражений являются формулы. Математика всегда была связана с вычислениями и формулами. Особенно много формул было получено при решении задач измерения – формулы вычисления длин, площадей, объемов простейших фигур. С помощью формул выражаются соотношения между различными величинами, как переменными, так и постоянными. Например, После того, как в науку вошли переменные величины, были изучены траектории движущихся точек, была создана буквенная алгебра, внимание ученых обратилось к изучению соответствий между величинами. С помощью координат удалось изобразить эти соответствия графически. Поэтому у Декарта и у его современников понятие функции было изложено на языке геометрии. Термин «функция» (от лат «функтус» - выполнять) был впервые использован Лейбницем (1692 год). В начале 19 века было дано определение числовой функции «Переменная величина y называется функцией переменной величины x, если каждому значению величины x соответствует единственное определенное значение величины y». В теме 3 мы вернемся к этому определению и его уточнению.
Поиск по сайту: |
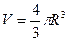 - формула объема шара, S=v*t – формула равномерного прямолинейного движения и пр.
- формула объема шара, S=v*t – формула равномерного прямолинейного движения и пр.